a Kosínusová funkcia alebo cos funkcia je skrátka jednou zo šiestich Goniometrické funkcie základom trigonometrie. Kosínus v trigonometrii je daný ako pomer základne k prepone pravouhlého trojuholníka. Kosínusová funkcia je reprezentovaná ako Cos x, kde x je uhol, pre ktorý sa vypočíta kosínusový pomer. Z hľadiska funkcie môžeme povedať, že x je vstup alebo definičný obor kosínusovej funkcie.

Vo veľkej miere sa používa v širokom spektre predmetov, ako je fyzika, geometria a inžinierstvo, okrem iného všeobecne využívaním jeho periodickej povahy. Používa sa napríklad na definovanie vlnovej povahy zvukových vĺn, výpočty elektrického toku cez rovinný povrch atď. V tomto článku sa podrobne dozvieme o tom, čo je kosínusová funkcia, doména a rozsah kosínusovej funkcie, periódy a grafu kosínusovej funkcie.

Obsah

• Čo je to kosínusová funkcia?
• Cos v Unit Circle
• Graf kosínusovej funkcie
• Inverzná funkcia kosínusu
• Funkcia kosínusu v kalkule
• Identity funkcie Cos

Čo je to kosínusová funkcia?

Kosínusová funkcia je goniometrická funkcia, ktorá má v podstate periodický charakter. Funkcia kosínus je vyjadrená ako cos x, kde x je jeden z ostrých uhlov pravouhlého trojuholníka. Kosínusová funkcia nájde pomer bázy a prepony pre danú hodnotu x. Funkcia kosínus je skrátená ako cos(x) alebo cos(θ), kde x je uhol v radiánoch a theta θ je uhol v stupňa všeobecne. Funkciu kosínus možno definovať pomocou jednotkového kruhu, t. j. kruhu s jednotkovým polomerom, ako uvidíme neskôr v tomto článku. Má periodický charakter a svoje hodnoty opakuje po každom úplnom otočení uhlov. Na karteziánskej rovine ju možno označiť ako vektorovú zložku prepony rovnobežnú s osou x.

Definícia kosínusovej funkcie

Kosínusová funkcia je definovaná v pravouhlom trojuholníku ako pomer dĺžky strany susediacej s príslušným uhlom k dĺžke prepony. Matematicky kosínusová funkcia je daná ako

Cos x = Cos θ = Dĺžka základne/Dĺžka prepony = b/h = OB/OA

kde X je uhol v radiánoch a θ je ekvivalentný uhol v stupňoch.

Funkcia domény a rozsahu Cos

Vieme, že pre funkciu je doména prípustné vstupné hodnoty a rozsah je výstupná hodnota pre túto konkrétnu vstupnú alebo doménovú hodnotu. Môžeme teda predpokladať, že funkcia funguje ako procesor, ktorý prijíma vstup, spracováva ho a dáva konkrétny výstup. Doména a rozsah funkcie cos sú popísané nižšie:

• Doména kosínusovej funkcie: R t.j. množina všetkých reálnych čísel.
• Rozsah kosínusovej funkcie: [-1, 1], t.j. výstup sa mení medzi všetkými reálnymi číslami medzi -1 a 1.

Obdobie funkcie kosínusu

The funkciu má periodický charakter, t.j. opakuje sa po 2π alebo 360°. Inými slovami, opakuje sa po každom úplnom otočení. Periódou kosínusovej funkcie je teda úplná rotácia alebo uhol 360° (alebo 2π).

Recipročná funkcia kosínus

Recipročná funkcia kosínusu je známa ako sekanta funkciu resp sek v skratke. Matematicky je prevrátená funkcia kosínus daná ako

znak na int v jazyku Java

sek(θ) = 1/cos(θ)

Podľa pravidiel o Recipročné , ak vynásobíme Cos x s Sec x, súčin bude vždy 1.

Graf kosínusovej funkcie

Graf kosínusovej funkcie sa podobá grafu sínusovej funkcie so základným rozdielom, že pre x = 0 graf sinovej funkcie prechádza z počiatku, kým pri x = 0 prechádza graf kosínusovej funkcie z (0, 1) na y-osy. Nasleduje graf hodnoty kosínusovej funkcie, t.j. y = cos x

Vlastnosti diskutované vyššie je možné vidieť v grafe, ako je periodická povaha funkcie.

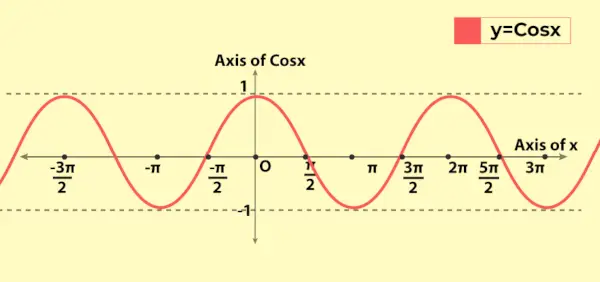
Variácia funkcie kosínusu v grafe

Keďže rozsah kosínusovej funkcie je [-1, 1], mení sa v grafe od -1 do 1. Prejavuje svoju periodickú povahu, keď sa graf opakuje po každej dĺžke 2π na osi x. To odráža, že kosínusová funkcia má periódu 2π (alebo 360°).

Cos v Unit Circle

Kosínusová funkcia môže byť definovaná pomocou jednotkového kruhu. Poďme pochopiť, ako môžeme definovať kosínusovú funkciu z hľadiska jednotkového kruhu.

Uvažujme úsečku OA otáčajúcu sa okolo bodu O, kde O je počiatok kartézskej roviny. Rotácia OA teda opisuje jednotkovú kružnicu (kružnicu s jednotkovým polomerom) so stredom v počiatku O a bod A vždy leží na tejto kružnici. Ak pustíme kolmicu z A na os x a priesečník nazveme B a θ je uhol, ktorý OA zviera s kladným smerom osi x, potom cos(θ) = projekcia prepony na x -os = OB/|OA| = OB (keďže |OA| = 1 jednotka).

Všimnite si, že smer OB je dôležitý, ako vidno na nasledujúcich obrázkoch. Zelený segment označuje dĺžku/veľkosť a šípka označuje smer (+ve alebo -ve) cos(θ)

Všimnite si, že hodnota cos(θ) je kladná pre θ patriace do prvého a štvrtého kvadrantu, kým záporná pre θ patriaca do druhého a tretieho kvadrantu.

Inverzná funkcia kosínusu

Inverzná funkcia kosínusovej funkcie známej ako arc-kosínus funkciu a skrátene ako arccos(x) alebo cos ^-1 (X) je definovaný nasledovne

cos(x) = y

⇒ cos ^-1 (y) = x

Doména a rozsah inverznej kosínusovej funkcie

Doména a rozsah inverznej kosínusovej funkcie sú uvedené nižšie:

• Doména inverznej kosínusovej funkcie: Všetky reálne čísla v rozsahu [-1, 1]
• Rozsah inverznej kosínusovej funkcie: Všetky reálne čísla v rozsahu [0, π]

Hyperbolická kosínusová funkcia

Hyperbolické funkcie sú analógovým ekvivalentom goniometrickej funkcie, ktorej algebraické vyjadrenie je v podmienkach exponenciálnej funkcie. Funkcia hyperbolického kosínusu skrátená ako cosh(x) kde X je hyperbolický uhol je pojem hyperbolickej geometrie. Podobne ako (cos(x), sin(x)) predstavuje bod na jednotkovej kružnici, (cosh(x), sinh(x)) predstavuje bod na jednotkovej hyperbole, t.j. xy = 1, kde sinh(x) predstavuje hyperbolický sínusová funkcia. Algebraický rozvoj hyperbolickej funkcie cos je daný ako

cosh(x) = (napr ^X + a ^-X )/2

Viac podrobností o hyperbolických funkciách presahuje rámec tohto článku, ale môžete sa na ne obrátiť tento článok .

Funkcia kosínusu v kalkule

Odvetvie počtu v matematike sa zaoberá diferenciácia a integrácia danej funkcie. Diferenciácia funkcie je rýchlosť zmeny funkcie vzhľadom na nezávislú premennú, zatiaľ čo integrácia je opačný proces diferenciácie, ktorý sa zaoberá hľadaním integrálu funkcie, ktorej derivácia existuje.

Derivácia kosínusovej funkcie

The derivát funkcie kosínus sa rovná záporu funkcie sínus. Matematicky

d(cos(x))/dx = -sin(x)

Integrácia kosínusovej funkcie

The neurčitý integrál funkcie kosínus sa rovná funkcii sínus. Matematicky -

∫cos(x)dx = sin(x) + C, kde C je integračná konštanta.

Funkcie sínus a kosínus

Nasledujúci graf predstavuje kľúčový rozdiel medzi funkciou sínus a kosínus:

Rozdiel medzi funkciami sínus a kosínus

Nasledujúca tabuľka uvádza rozdiely medzi funkciou sínus a kosínus –

Tabuľka hodnôt cos

Nasledujúca tabuľka poskytuje hodnoty kosínusovej funkcie pre niektoré spoločné uhly v prvom kvadrante kartézskej roviny –

Pomocou týchto hodnôt môžeme ľahko vypočítať hodnoty iných bežných uhlov ako 15°, 75°, 195°, -15° atď. pomocou vzorcov cos (x + y) a cos (x – y) popísaných ďalej v tomto článku. článok.

skontrolujte, Trigonometrická tabuľka

Identity funkcie Cos

Základné trigonometrické identity súvisiace s kosínusovou funkciou sú uvedené nižšie:

• bez²(x) + cos²(x) = 1
• cos(x + y) = cos(x)cos(y) – sin(x)sin(y)
• cos(x – y) = cos(x)cos(y) + sin(x)sin(y)
• cos(-x) = cos(x)
• cos(x) = 1/s(x)
• cos 2x = cos²x – hriech²x = 1 – 2 sin²x = 2 cos²x – 1 = (1 – tan²x/1 + tan²X)
• cos 3x = 4cos³x – 3 cos x

Súvisiace články

• Diferenciácia goniometrických funkcií
• Inverzné goniometrické funkcie
• Inverzné trig deriváty

Vyriešené príklady kosínusovej funkcie

Tu je niekoľko vyriešených príkladov, ktoré vám pomôžu lepšie pochopiť pojem kosínusová funkcia.

Príklad 1: Aké sú maximálne a minimálne hodnoty kosínusovej funkcie?

Riešenie:

Maximálna hodnota kosínusovej funkcie je 1 pri 0° a 180°, pričom minimálna hodnota funkcie je -1 pri 180°.

Príklad 2: Pod akým uhlom (uhlmi) v rozsahu [0, 360] je hodnota kosínusovej funkcie 0?

Riešenie:

Hodnota kosínusovej funkcie je 0 pri uhloch 90° a 270°.

Príklad 3: Pre ktoré kvadranty je hodnota kosínusovej funkcie záporná?

Riešenie:

Kosínusová funkcia je negatívna v II^nda III^rdkvadrantoch.

Príklad 4: Vypočítajte hodnotu cos (45°).

Riešenie:

čo je príkaz export v linuxe

Podľa identity 4 uvedenej vyššie, cos(-x) = cos(x).

Preto cos(-45°) = cos(45°) = 1/√2

Príklad 5: Vypočítajte hodnotu cos(15°).

Riešenie:

Použitie identity 3 uvedenej vyššie –

cos(15degree) = cos(45degree – 30degree) ewline = cos(45degree)cos(30degree) + sin(45degree)sin(45degree) ewline = frac{1}{sqrt2} imesfrac{sqrt3}{2} + frac{1}{sqrt2} imes frac{1}{2} ewline = frac{sqrt3 + 1}{2sqrt2}

Príklad 6: Čo je cos ^-1 (1/2) v rozsahu [0,π]?

Riešenie:

Nechajte čos^-1(1/2) = y.

Preto cos(y) = 1/2 ⇒ y = π/3 vo vyššie uvedenom rozsahu.

Odpoveď je teda π/3.

Príklad 7: Aká je hodnota cos(-15°)?

Riešenie:

Použitie identity 3 uvedenej vyššie –

cos(-15degree) ewline = cos(30degree – 45degree) ewline = cos(30degree)cos(45degree) + sin(30degree)sin(45degree) ewline = frac{sqrt3}{2} imesfrac{1}{sqrt{2}} + frac{1}{2} imesfrac{1}{sqrt2} ewline = frac{sqrt3 + 1}{2sqrt2} .

Alternatívne môžeme použiť aj identitu cos(-x) = cos(x) a použiť hodnotu cos(15°) vypočítanú v príklade 5.

Príklad 8: Vypočítajte plochu pod grafom kosínusovej funkcie pre x = 0 až x = π/2.

Riešenie:

Danú plochu možno vypočítať riešením nasledujúceho určitého integrálu –

int_0^{frac{pi}{2}}cos(x)dx ewline = sin(frac{pi}{2}) – sin(0) ewline = 1 – 0 ewline = 1

Preto je odpoveď 1 štvorcová jednotka.

Príklad 9: Ak cos(x) = π/3, nájdite hodnotu cos(3x) (v desiatkovom tvare s presnosťou na dve desatinné miesta).

Riešenie:

Pomocou identity – cos(3x) = 4cos³(x) – 3 cos (x) –

cos(3x) = 4⨉(π/3)³-3⨉(π/3) ≅ 4,59 – π = 1,45

Príklad 10: Nájdite hodnotu cos(120°).

Riešenie:

Použitie identity pre cos (2x)

cos(120°) = cos(2⨉60°) = 1 – 2 sin²(60°) = 1-2⨉(√3/2)²= 1 – 3/2 = -1/2

Cvičné otázky: Cos funkcie

Q1. Aký je vzorec na výpočet cos uhla v pravouhlom trojuholníku?

Q2. Aká je geometrická interpretácia cos v karteziánskej rovine?

Q3. Vypočítajte hodnotu cos(120°).

Q4. Nájdite hodnotu cos ^-1 (√3/2) v rozsahu [π, 2π].

Q5. Ak pól vrhá na zem tieň rovnakej dĺžky, nájdite uhol slnka vzhľadom na zem, ak je slnko na východ.

Zhrnutie – Kosínusová funkcia

Funkcia kosínus, označovaná ako cos(x), je základná trigonometrická funkcia definovaná ako pomer základne k prepone v pravouhlom trojuholníku a je nevyhnutná v rôznych oblastiach, ako je fyzika, inžinierstvo a geometria, kvôli jej periodickej povahe. , ktorý je nápomocný pri modelovaní správania vĺn. Má doménu všetkých reálnych čísel a rozsah od -1 do 1, pričom cyklus sa opakuje každé 2 Pi radiánov alebo 360 stupňov, zrejmé z jeho vlnovitého grafu, ktorý začína na (0,1). Z hľadiska počtu je derivácia cos(x) − sin( X ), a jeho integrál dáva sin( X )+ C s C ako integračnou konštantou. Táto funkcia sa rozširuje aj na hyperbolické formy, ako je cosh(x), čím sa zlepšuje jej aplikácia v rôznych matematických kontextoch a riešeniach, vrátane výpočtov vĺn a oscilácií vo fyzikálnych systémoch.

Funkcia kosínusu: často kladené otázky

1. Čo je to kosínusová funkcia?

Funkcia kosínus je jednou zo základných goniometrických funkcií. Je definovaný v pravouhlom trojuholníku ako pomer dĺžky strany susediacej s príslušným uhlom k dĺžke prepony.

2. Sú cos a kosínus rovnaké v trigonometrii?

Áno. cos je skratka/skrátená forma funkcie kosínus.

3. Čo je to rozsah funkcie Cos?

Rozsah funkcie cos alebo kosínus sú všetky reálne čísla v rozsahu od -1 do 1, t.j. [-1,1].

4. Čo je doména funkcie Cos?

Definičný obor funkcie cos alebo kosínus je sérom všetkých reálnych čísel, t.j. R .

5. Aká je maximálna hodnota kosínusovej funkcie?

Maximálna hodnota kosínusovej funkcie je 1 pre všetky uhly ekvivalentné 0° alebo 360°.

6. Aká je minimálna hodnota kosínusovej funkcie?

Minimálna hodnota kosínusovej funkcie je -1 pre všetky uhly ekvivalentné 180°.

7. Ako zistiť hodnotu Cos(-x)?

Hodnotu cos(-x) možno vypočítať výpočtom hodnoty cos(x) v dôsledku existencie nasledujúcej identity: cos(-x) = cos(x).

8. Ako vykresliť funkciu kosínusu?

Ak chcete nakresliť graf funkcie kosínus v kartézskej rovine, os x predstavuje uhly v radiánoch (alebo stupňoch) a os y predstavuje hodnotu kosínusovej funkcie pre zodpovedajúci uhol na osi x. teraz

• Krok 1: Vezmite podmnožinu osi x, pre ktorú by ste chceli nakresliť graf.
• Krok 2: Rozdeľte os x v tomto rozsahu na ekvidištantné body (t. j. medzi všetkými podbodmi je rovnaký priestor). Všimnite si, že čím väčší je počet dielikov, tým väčšia je presnosť výsledného grafu.
• Krok 3: Pre každý z týchto čiastkových bodov x označte bod (x, cos(x)) na grafe.
• Krok 4: Spojte všetky označené body, aby ste získali graf kosínusovej funkcie (pre podmnožinu osi x, ktorú ste vybrali).

9. Ako nájsť periódu kosínusovej funkcie?

Perióda kosínusovej funkcie sa vzťahuje na minimálny rozsah hodnôt, po ktorých sa funkcia začne opakovať. Vieme, že kosínusová funkcia sa opakuje po každej úplnej rotácii, čo znamená 2π radiány. Preto je perióda kosínusovej funkcie 2π radiány alebo 360°.

10. Čo je amplitúda kosínusovej funkcie?

Amplitúda kosínusovej funkcie sa týka maximálneho posunutia hodnoty funkcie od strednej polohy, t.j. osi x. Amplitúda kosínusovej funkcie je 1, pretože maximálny posun je 1 (pre hodnoty -1 a 1 pri 180 a 0 stupňoch. Všimnite si, že rozsah kosínusovej funkcie je [-amplitúda, amplitúda].