A Funkcia v matematike je špeciálny vzťah medzi množinou vstupných hodnôt a množinou výstupných hodnôt. Vo funkcii každá vstupná hodnota dáva konkrétnu výstupnú hodnotu. Funkciu v matematike reprezentujeme ako, y = f(x) kde X je vstupná hodnota a pre každú X dostaneme výstupnú hodnotu ako y.

V tomto článku sa dozvieme, funkcie v matematike, ich rôzne druhy, príklady a iné podrobne.

Obsah

• Čo je funkcia v matematike?
• Definícia funkcie v matematike
• Príklady funkcií
• Podmienka pre funkciu
• Reprezentácia funkcií v matematike
• Identifikácia funkcie
• Typy funkcií
• Čo je funkcia v algebre?
• Doména a rozsah funkcie
• Zloženie funkcií
• Algebra funkcií
• Čo je funkcia v grafe?
• Grafické funkcie
• Spoločné funkcie
• Aplikácie funkcií
• Príklady funkcie
• Cvičte problémy o tom, čo je funkcia

Čo je funkcia v matematike?

Funkcia v matematike je a vzťah medzi vstupnými hodnotami (doména) a výstupnými hodnotami (rozsahom) daných množín tak, že žiadne dve premenné z množín domén nie sú spojené s rovnakou premennou v množine rozsahov. Jednoduchý príklad funkcie v matematike je f(x) = 2x, ktorá je definovaná na R→R, tu akákoľvek premenná v doméne súvisí iba s jednou premennou v rozsahu.

Funkcia v matematike má doménu, kodoménu a rozsah. Definícia je množina všetkých možných hodnôt x a rozsah funkcie je množina všetkých výstupných hodnôt y. Rozsah je podmnožinou kódovej domény funkcie. Môžeme tiež povedať, že funkcia v matematike je vzťah s jedinečným výstupom a žiadne dve vstupné hodnoty nemajú podobný výstup vo funkcii, ako je to v prípade vzťahu.

Definícia funkcie v matematike

Funkcia je špeciálny vzťah alebo metóda spájajúca každý člen množiny A s jedinečným členom množiny B prostredníctvom definovaného vzťahu. Množina A sa nazýva doména a množina B sa nazýva kodoména funkcie. Funkcia v matematike z množiny A do množiny B je definovaná ako,

f = ∀ a ∈ A, b ∈ B

Každá funkcia je relácia, ale každá relácia nie je funkciou. Kritériá pre akýkoľvek vzťah, ktorý sa má považovať za funkciu, pretože vo funkcii má každý prvok množiny A iba jeden obraz v množine B, zatiaľ čo vo vzťahu môže mať prvok množiny A viac ako jeden obraz v množine B.

V matematike definujeme funkcie z neprázdnej množiny A do neprázdnej množiny B tak, že:

(a, b) ∈ f, potom f(a) = b

kam sme volali b ako obraz a definovaný pod vzťahom f .

Každý prvok „a“ zo sady A má jedinečný obraz “ b “ v množine B je to funkcia.

Príklady funkcií

Funkcia v matematike f je definovaná ako, y = f(x) kde X je vstupná hodnota a pre každú vstupnú hodnotu x dostaneme jedinečnú hodnotu y. Rôzne príklady funkcií v matematike definovaných na R→R sú,

• y = f(x) = 3x + 4
• y = f(x) = sin x + 3
• y = f(x) = -3x²+ 3 atď

Podmienka pre funkciu

Pre ľubovoľné dve neprázdne množiny A a B funkcia f: A→B označuje to f je funkcia od A do B, kde A je doména a B je spoločná doména.

Pre ľubovoľný prvok a ∈ A, jedinečný prvok, b ∈ B existuje také, že (a,b) ∈ f. Jedinečný prvok b, ktorý súvisí s a, sa označuje ako f(a) a číta sa ako f z a. To možno lepšie pochopiť z obrázku nižšie:

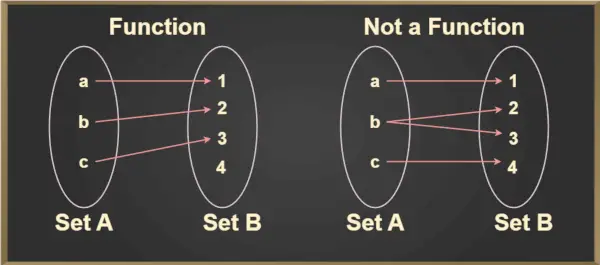
Test zvislej čiary

Test zvislej čiary sa používa na určenie, či je krivka funkciou alebo nie. Ak akákoľvek krivka pretína zvislú čiaru vo viac ako jednom bode, potom krivka nie je funkciou.

Reprezentácia funkcií v matematike

Funkciu v matematike reprezentujeme ako,

y = f(x) = x + 3

Tu je množina hodnôt x doménou funkcie a množina výstupných hodnôt y kodoménou funkcie. Tu je funkcia definovaná pre všetky reálne čísla, pretože dáva jedinečnú hodnotu pre každé x, ale nie vždy je možné získať výstup pre každú hodnotu x v takom prípade definujeme funkciu v dvoch častiach, možno to chápať ako

• f(x) = 1/(x – 2), kde x ≠ 2
• f(x) = x²kde x ∈ {R}

Funkciu v matematike môžeme definovať ako stroj, ktorý odoberá určitý vstup a dáva jedinečný výstup. Funkcia f(x) = x²je definovaný nižšie ako,

Funkciu v matematike môžeme reprezentovať tromi metódami ako,

• Sada objednaných párov
• Tabuľkový formulár
• Grafická forma

Napríklad, ak reprezentujeme funkciu ako, f(x) = x³

Ďalším spôsobom, ako reprezentovať rovnakú funkciu, je ako sada objednaných párov ako,

f = {(1,1), (2,8), (3,27)}

Vo vyššie uvedenej množine je definičný obor funkcie D = {1, 2, 3} a rozsah funkcie je R = {1, 8, 27}

Identifikácia funkcie

Funkcia je klasifikovaná ako špeciálny typ vzťahu v matematike. Existujú nasledujúce pravidlá, ktoré možno použiť na identifikáciu funkcie:

• Vzťah, v ktorom každý vstup mapovaný na jedinečný výstup je funkcia. Toto vyvolalo funkciu jedna k jednej.
• Vzťah, v ktorom dva vstupy (predobraz) mapované na jeden výstup sú tiež funkciou. Toto je mnoho funkcií.
• Vzťah, v ktorom je jeden vstup mapovaný na dva rôzne výstupy, nie je funkciou.
• Vzťah, v ktorom je veľa vstupov mapovaných na veľa výstupov podľa žiadneho špecifického pravidla, nie je funkciou.

Typy funkcií

Rôzne Typy funkcií sa používajú na riešenie rôznych typov matematických problémov týkajúcich sa najmä kriviek a rovníc. V matematike existujú tri hlavné typy funkcií, ktoré sú založené na mapovaní prvkov z množiny A do množiny B.

Injektívna funkcia alebo funkcia jedna ku jednej

Funkcia, v ktorej má každý prvok domény odlišný obraz v kodéne, sa nazýva Injektívne alebo Funkcia one-to-one .

f: A → B sa označuje ako jedna ku jednej alebo injekčné, ak sú obrazy odlišných prvkov A pod f odlišné, t.j.

f(a ₁ ) = b ₁ , f(a ₂ ) = b ₂

kde₁, a₂∈ A a b₁, b₂∈ B

Surjektívne funkcie alebo Onto Function

Surjective Function je funkcia, v ktorej má každý prvok kodomény predobraz v doméne. Je to aj tzv Na Funkciu čo znamená, že každý prvok kodomény je spojený s každým prvkom domény. Žiadny prvok kodomény by nemal mať prázdny vzťah. Počet prvkov kodomény a rozsah je rovnaký.

f: A → B sa nazýva on, ak každý prvok B je obrazom nejakého prvku A pod f, t.j. pre každé b ϵ B existuje prvok „a“ v A taký, že f(a) = b.

Bijektívna funkcia

Ak má funkcia vlastnosti Injective (One to One) a Surjective (Onto function), potom sa funkcia nazýva Bijektívna funkcia . V bijektívnej funkcii každý prvok domény súvisí s každým prvkom kodomény a tiež existuje vzťah jedna k jednej. To znamená, že počet prvkov kodomény a rozsah sú rovnaké a žiadny prvok v doméne ani v kodoméne nemá prázdny vzťah.

Na základe výstupných hodnôt sú funkcie klasifikované ako nepárne a párne funkcie. Poďme sa na ne pozrieť

Nepárne funkcie

Nepárna funkcia je typ funkcie, ktorá vykazuje symetriu pôvodu. Konkrétne, ak je f(x) nepárna funkcia, ukazuje, že f(-x) = -f(x)

Rovnomerná funkcia

Párna funkcia je typ funkcie, ktorá vykazuje symetriu okolo osi y. Konkrétne, ak f(x) je párna funkcia, ukazuje, že f(-x) = f(x)

Čo je funkcia v algebre?

Funkcia v algebra je rovnica, pre ktorú každé x, ktoré možno vložiť do rovnice, vytvorí presne jeden výstup, napríklad y, z rovnice. Je reprezentovaný ako y = f(x), kde x je nezávislá premenná a y je závislá premenná.

Napríklad:

priemer vs priemer

• y = 2x + 1
• y = 3x – 2
• y = 4 roky
• y = 5/x

Doména a rozsah funkcie

Doména a rozsah funkcie sú vstupná a výstupná hodnota funkcie. Povedzme napríklad, že máme funkciu danú ako f(x) = x². Tu môžeme brať všetky reálne čísla ako vstupnú hodnotu x a výstupom bude vždy kladné reálne číslo. Jeho doménou je teda množina všetkých reálnych čísel reprezentovaných ako R, zatiaľ čo jej rozsah je množina kladných reálnych čísel reprezentovaných ako R⁺

Zloženie funkcií

Ak f: A → B a g: B → C sú dve funkcie. Potom sa zloženie f a g označí ako f(g) a je definované ako funkcia hmla = f(g(x)) pre x ∈ A.

Zoberme si dve funkcie f(x) = x + 3 a g(x) = 2x²

hmla = f(g(x))

⇒ hmla = f(2x²)

⇒ zub = 2x²+ 3

Uč sa viac, Zloženie funkcie

Algebra funkcií

Algebra funkcií zahŕňa algebraické operácie vykonávané medzi dvoma funkciami. Algebraické operácie pre dve funkcie f(x) a g(x) definované na skutočnej hodnote x sú uvedené nižšie:

• (f + g) (x) = f(x) + g(x)
• (f – g) (x) = f(x) – g(x)
• (f.g) (x) = f(x).g(x)
• (kf(x)) = k (f(x)); {Pre, k je reálne číslo}
• (f/g)(x) = f(x)/g(x); {Pre g(x) ≠ 0}

Čo je funkcia v grafe?

Funkciu je možné jednoducho znázorniť v grafe. Akákoľvek funkcia na grafe predstavuje krivku (vrátane priamky) v rovine x-y mapovanú pre jej vstupné a zodpovedajúce výstupné hodnoty.

Ak chcete nakresliť funkciu na a, nájdite niekoľko bodov, ktoré ležia na funkcii, a potom tieto body spojte podľa miesta funkcie. Napríklad na zobrazenie funkcie (priamka) f(x) = y = 5x – 2 potrebujeme nejaký bod na grafe. Aby sme našli bod, bod na grafe, najprv vezmeme náhodné hodnoty x a potom nájdeme ich zodpovedajúce hodnoty y, ako

f(x) = y = 5x-2

ak x = 0, y = 5(0) – 2 = -2 ⇒ (x, y) = (0, -2)

ak x = 1, y = 5 (1) – 2 = 3 ⇒ (x, y) = (1, 3)

ak x = 2, y = 5(2) – 2 = 8 ⇒ (x, y) = (2, 8)

Spojením týchto bodov dostaneme graf funkcie y = 5x – 2

Grafické funkcie

Poznanie hodnôt x umožňuje zobrazenie funkcie f(x) v grafe. Pretože y = f(x), môžeme nájsť súvisiacu hodnotu pre y tak, že začneme s hodnotami x. V dôsledku toho môžeme vykresliť graf v rovine súradníc pomocou hodnôt x a y. Zvážte nasledujúci scenár:

Predpokladajme, že y = x + 3

Keď x = 0, y = 3

podobne,

• x = -2, y = -2 + 3 = 1
• x = -1, y = -1 + 3 = 2
• x = 1, y = 1 + 3 = 4
• x = 2, y = 2 + 3 = 5
• x = 3, y = 3 + 3 = 6

Výsledkom je, že pomocou týchto hodnôt môžeme vykresliť graf pre funkciu x + 3.

Spoločné funkcie

Niektoré bežné funkcie, ktoré sa bežne používajú v matematike, sú popísané nižšie:

Skutočná funkcia

Skutočná funkcia v matematike označuje funkciu, ktorej doménou a rozsahom sú podmnožiny reálnych čísel (označené ako ℝ). Zjednodušene povedané, reálna funkcia je matematické pravidlo alebo vzťah, ktorý priraďuje hodnotu reálneho čísla každému vstupu reálneho čísla.

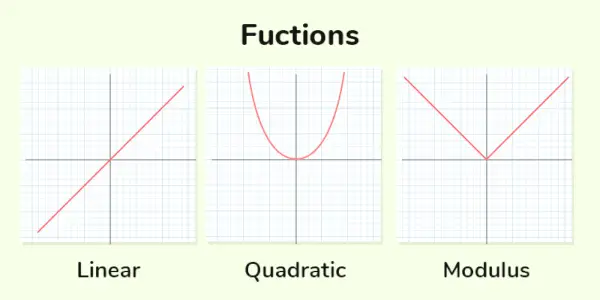
Skutočné funkcie

Polynomická funkcia

Funkcia, v ktorej sú exponenty algebraických premenných nezáporné celé čísla, sa nazýva Polynomická funkcia . Ak je mocnina premennej 1, nazýva sa to lineárna funkcia, ak je mocnina 2, nazýva sa kvadratická funkcia a ak je mocnina 3, nazýva sa kubická funkcia. Niektoré príklady polynomických funkcií sú uvedené nižšie:

• y = x²
• y = 2x + 3
• y = 3x³

Polynomické funkcie možno ďalej rozdeliť do nasledujúcich typov:

Lineárna funkcia : Lineárne funkcie sú tie, v ktorých maximálna mocnina premennej je 1. Všeobecná forma Lineárna funkcia je y = mx + c

Kvadratická funkcia : Kvadratická funkcia je taká, v ktorej maximálna mocnina premennej je 2. Všeobecná forma kvadratickej funkcie je, sekera ² + bx + c = 0

Kubická funkcia : Kubická funkcia sú tie, v ktorých je maximálna mocnina premennej 3. Všeobecný Tvar kubickej funkcie je daný ako sekera ³ + bx ² + cx + d = 0

Inverzná funkcia

Inverzná funkcia je funkcia obsahujúca inverziu inej funkcie. Povedzme, že máme funkciu y = f(x), potom jej inverzná funkcia bude x = f^-1(y). V y = f(x) je doména x a rozsah je y, zatiaľ čo v prípade x = f^-1(y), doména je y a rozsah je x. Môžeme teda povedať, že definičný obor pôvodnej funkcie je obor jej inverznej funkcie a obor pôvodnej funkcie je definičný obor pôvodnej funkcie. Niektoré príklady inverzných funkcií sú napr.

• y = tak^-1(X)
• y = x^-1

Funkcia oblasti

Funkcia plochy sa zvyčajne vzťahuje na matematickú funkciu, ktorá vypočítava plochu geometrického tvaru alebo oblasti. Funkcia plochy berie ako vstup jeden alebo viac parametrov a vracia plochu zodpovedajúceho tvaru. Niektoré funkcie oblasti sú popísané nižšie:

Oblasť funkcie kruhu : Oblasť kruhu (A) je funkciou jeho polomeru(r) tak, že:

A = πr ²

Oblasť funkcie trojuholníka : Oblasť trojuholníka (A) je funkciou jeho základne (b) a výšky (h) tak, že:

A = (bh)/2

Exponenciálna funkcia

Exponenciálna funkcia je ten, ktorý je reprezentovaný ako f(x) = e^X. Často sa používa na zobrazenie rýchleho rastu alebo rozpadu.

Logaritmická funkcia

Logaritmická funkcia je matematická funkcia, ktorá predstavuje inverznú operáciu umocňovania. Je reprezentovaný ako f(x) = log x.

Funkcia stropu

Stropná funkcia , označené ako ⌈x⌉, zaokrúhľuje reálne číslo x nahor na najbližšie celé číslo, ktoré je väčšie alebo rovné x. Inými slovami, nájde najmenšie celé číslo, ktoré je väčšie alebo rovné x.

Funkcia podlahy

Funkcia spodnej hranice, označená ako ⌊x⌋, zaokrúhli reálne číslo x nadol na najbližšie celé číslo, ktoré je menšie alebo rovné x. Inými slovami, nájde najväčšiu celočíselnú hodnotu, ktorá je menšia alebo rovná x.

Modulová funkcia

Modulová funkcia , tiež známa ako funkcia absolútnej hodnoty, vracia veľkosť alebo veľkosť reálneho čísla bez ohľadu na jeho znamienko. Modulová funkcia je označená ako ∣x∣, kde x je vstupná hodnota.

Funkcia Signum

Funkcia Signum , tiež známa ako funkcia znamienka alebo funkcia znamienok, je matematická funkcia, ktorá vracia znamienko reálneho čísla. Označuje, či je číslo kladné, záporné alebo nulové.

Goniometrické funkcie

Goniometrické funkcie sú matematické funkcie, ktoré spájajú uhly pravouhlého trojuholníka s dĺžkami jeho strán. Šesť primárnych goniometrických funkcií je sínus (sin), kosínus (cos), tangens (tan), kosekans (cosec), secans (sec) a kotangens (cot).

Komplexné funkcie

Každá funkcia, v ktorej je vstupná premenná komplexnou funkciou, sa nazýva komplexná funkcia. Komplexné číslo je číslo, ktoré možno vykresliť v komplexnej rovine. V komplexné číslo máme reálne číslo a imaginárne číslo. Komplexné číslo (z) je reprezentované ako, z= x + iy a komplexná funkcia je reprezentovaná ako, f(z) = P(x, y) + iQ(x, y)

Aplikácie funkcií

Keď hovoríme, že premenná veličina y je funkciou premennej veličiny x, naznačujeme, že y závisí od x a že hodnota y je určená hodnotou x. Táto závislosť môže byť vyjadrená nasledovne: f = y (x).

• Polomer kruhu možno použiť na výpočet plochy kruhu. Polomer r ovplyvňuje oblasť A. Vyhlasujeme, že A je funkciou r v matematickom jazyku funkcií. Môžeme napísať A = f(r) =π×r²
• Objem gule V je funkciou jej polomeru. V = f(r) = 4/3 x r³označuje závislosť V na r.
• Sila je funkciou zrýchlenia telesa s pevnou hmotnosťou m. F = g(a) = mxa.

Ľudia tiež čítajú:

• Vzťah a funkcia
  
• Doména a rozsah goniometrických funkcií
• Rozsah funkcie
• Hyperbolická funkcia

Príklady funkcie

Príklad 1: Pre dve funkcie f a g sú definované ako, f(x) = x ² a g(x) = ln(2x). Nájdite zloženú funkciu (gof)( x)

Riešenie:

Vzhľadom na to:

• f(x) = x²
• g(x) = ln(2x)

(gof )( x ) = g (f (x))

[g (f (x)] = ln (2f (x))

= ln(2x²)

= 2 ln (√2x)

Teda (gof)(x) = 2 ln(√2x)

Príklad 2: Nájdite výstup funkcie g(t)= 6t ² + 5 o

• (i) t = 0
• (ii) t = 2

Riešenie:

Daná funkcia,

g(t) = 6t²+ 5t

• (i) t = 0

g(0) = 6(0)²+5(0) = 0 + 0

g(0) = 0

• (ii) t = 2

g(2) = 6(2)²+5(2)

g(2) = 24 + 10

g(2) = 34

Príklad 3: Dĺžka obdĺžnika je päťnásobok jeho šírky, vyjadrite obsah obdĺžnika ako funkciu jeho dĺžky.

Riešenie:

Nech je dĺžka obdĺžnika l a šírka obdĺžnika je b

teraz

• b = l/5

Plocha obdĺžnika (A) = l × l/5 = l²/5

Plocha obdĺžnika ako funkcia jeho dĺžky je teda

A(l) = l ² /5

Cvičte problémy o tom, čo je funkcia

1. Daná funkcia f(x)=3x+5

• Nájsť f(2)
• Nájsť f(−1)
• Určte definičný obor a rozsah funkcie.

2. Daná funkcia g(x)=x ² - 4x + 3

• Nájdite korene funkcie.
• Nájdite g(3) a g(0).
• Určte vrchol funkcie.

3. Dané dve funkcie f(x)=x + 2 a h(x)=2x – 3

• Nájdite zloženú funkciu (f ∘ h) (x)
• Vyhodnotiť (f ∘ h) (2)

Zhrnutie – Čo je funkcia

Funkcia v matematike je špeciálny vzťah medzi vstupnými hodnotami (doména) a výstupnými hodnotami (rozsah), kde je každý vstup spojený s jedinečným výstupom. Funkcie reprezentované ako y = f(x) majú špecifické vlastnosti a možno ich vizualizovať pomocou usporiadaných párov, tabuliek alebo grafov. Sú nevyhnutné v rôznych matematických problémoch a prichádzajú v rôznych typoch vrátane injektívnych (jedna k jednej), surjektívnej (na jednej) a bijektívnej (oba). Funkcie možno testovať pomocou testu zvislej čiary a ďalej sa delia na polynomické, inverzné, exponenciálne, logaritmické a trigonometrické funkcie. Pochopenie funkcií zahŕňa rozpoznanie ich domény, rozsahu a pravidiel, ktoré ich definujú. Príklady zahŕňajú jednoduché lineárne funkcie ako napr y = 2x + 1 a komplexné zloženie funkcií. Funkcie zohrávajú kľúčovú úlohu v algebre, geometrii a počte, pomáhajú pri reprezentácii a analýze matematických vzťahov a javov v reálnom svete.

Časté otázky o tom, čo je funkcia

Aká je definícia funkcie?

Vzťah f definovaný na množine A k inej množine B sa v matematike nazýva funkcia, ak každá hodnota A má jedinečnú hodnotu v množine B.

Ako napísať funkciu v matematike?

Funkcia f v matematike je reprezentovaná ako f: A → B a je definovaná ako, f(x) = x + 2. Tu pre každú jedinečnú hodnotu x máme jedinečnú hodnotu y.

Ako transformovať funkciu?

Funkciu môžeme ľahko transformovať na iné funkcie jednoduchým vykonaním základných algebraických operácií s funkciou. Rôzne transformácie funkcie sú odraz, translácia, rotácia atď.

Čo je to racionálna funkcia?

Zlomková funkcia, kde čitateľ a menovateľ sú polynomické funkcie, sa nazýva racionálna funkcia. Niektoré príklady racionálnej funkcie sú napr.

• f(x) = x ² /(2x + 3)
• g(x) = (6x + 3)/(x – 1), atď.

Čo je to lineárna funkcia?

Algebraická funkcia, v ktorej je každý člen funkcie buď konštantný, alebo má mocninu jednej, sa nazýva lineárna funkcia. Niektoré príklady lineárnej funkcie sú napr.

• f(x) = 2x + 3
• g(x) = x – 5 atď.

Čo je doména a kódová doména funkcie?

Ak funkciu definujeme ako, y = f(x). Potom doménou x sú všetky hodnoty x, pre ktoré y vedie k jedinečnej hodnote. A ko-doména y je množina všetkých hodnôt y pre každú hodnotu x.

Ako identifikujete funkciu v matematike?

Ak má akákoľvek vstupná hodnota (x) domény vo vzťahu viac ako jeden obrázok (y), potom tento vzťah nemôže byť nikdy funkciou. Takže ak sa hodnota x opakuje v usporiadanom páre, potom to nikdy nie je funkcia.