TRIGONOMETRICKÁ TABUĽKA

Trigonometrická tabuľka je štandardná tabuľka, ktorá nám pomáha nájsť hodnoty trigonometrických pomerov pre štandardné uhly ako 0°, 30°, 45°, 60° a 90°. to pozostáva zo všetkých šiestich trigonometrických pomerov: sínus, kosínus, tangens, kosekans, sekans a kotangens.

Dozvieme sa podrobnejšie o trigonometrickej tabuľke.

Obsah

Trigonometrická tabuľka
Tabuľka goniometrických funkcií
Trik, ako sa naučiť trigonometrické pomery
Ako si zapamätať trigonometrickú tabuľku
Ako vytvoriť tabuľku spúšťania
Trigonometrické vzorce
Tabuľka goniometrických identít
Príklady trigonometrickej tabuľky

Goniometrická tabuľka je usporiadanie hodnôt všetkých šiestich goniometrických funkcií pre ich spoločné uhly v tabuľkovej forme.

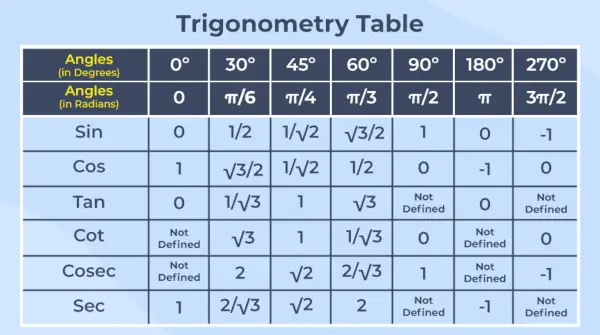
Trigonometrická tabuľka

Poznámka – Trigonometria je časť matematiky, ktorá sa zaoberá vzťahmi medzi uhlami a stranami pravouhlých trojuholníkov.

Tabuľka goniometrických funkcií

Trigonometria má 6 základných goniometrických funkcií, ktorými sú sínus, kosínus, tangens, kosekans, sekans a kotangens. Teraz sa pozrime na goniometrické funkcie.

Pre každý pravouhlý trojuholník s kolmicou (P), základňou (B) a preponou (H) je šesť goniometrických funkcií nasledujúcich:

Tabuľka goniometrických funkcií
Funkcia	Definícia	zastupovanie	Vzťah k stranám pravého trojuholníka
Jeho	Pomer kolmice a prepony	bez i	Opačná strana / prepona
Kosínus	Pomer bázy a prepony	cos i	Priľahlá strana / prepona
Tangenta	Pomer sínusu a kosínusu uhla	tak i	Opačná strana / Susedná strana
Cosecant	Obojstrannosť hriechu θ	csc i alebo cosec i	Prepona / Opačná strana
Secant	Prevrátená hodnota cos θ	sek i	Prepona / Priľahlá strana
Kotangens	Prevrátená hodnota tan θ	detská postieľka i	Priľahlá strana / Opačná strana

Poznámka – Trigonometria je odvetvie matematiky, ktoré sa zaoberá vzťahmi medzi uhlami a stranami trojuholníkov, najmä pravouhlých trojuholníkov. Zahŕňa štúdium a aplikáciu sínusových, kosínusových, tangensových a iných goniometrických funkcií na riešenie problémov v rôznych oblastiach.

Skontrolujte : Trigonometria: Vzorce, Tabuľka, Identity a pomery

Trik, ako sa naučiť trigonometrické pomery

Preštudujte si nižšie diskutovanú tabuľku, aby ste sa naučili trigonometrické pomery ľahko zapamätateľným spôsobom.

Niektorí ľudia majú kučeravé čierne vlasy na výrobu krásy

sin θ (niektorí) = kolmá (ľudia) / prepona (majú)

cos θ (kučeravé) = základňa (čierna) / prepona (vlasy)

opálenie θ (do) = kolmá (výroba) / základňa (krása)

Ako si zapamätať trigonometrickú tabuľku

Trigonometrická tabuľka je celkom ľahko zapamätateľná, ak poznáte všetky trigonometrické vzorce. Existuje aj trik s názvom trik s jednou rukou zapamätať si trigonometrickú tabuľku.

Ako si zapamätať trigonometrickú tabuľku

Krok 1: Na obrázku vyššie pre sínusovú tabuľku spočítajte prsty na ľavej strane pre štandardný uhol.

Krok 2: Počet prstov na ľavej strane (vypočítajte v 1. kroku) vydeľte 4

Krok 3: Nájdite druhú odmocninu hodnoty vypočítanej v kroku 2.

Skontrolujte: Trigonometrické vzorce – zoznam všetkých trigonometrických identít a vzorcov

Ako vytvoriť tabuľku spúšťania

Preštudujte si nasledujúce kroky na vytvorenie trigonometrickej tabuľky pre štandardné uhly.

Krok 1: Vytvorte tabuľku

Vytvorte tabuľku a vypíšte všetky uhly ako napr 0°, 30°, 45°, 60° a 90°, v hornom rade. Do prvého stĺpca zadajte všetky trigonometrické funkcie sin, cos, tan, cosec, sec a cot.

Krok 2: Vyhodnoťte hodnotu pre všetky uhly funkcie sin.

Ak chcete nájsť hodnoty funkcie sin, vydeľte 0, 1, 2, 3 a 4 4 a vezmite pod koreň každej hodnoty, resp.

Pre hodnotu sin 0° = √(0/4) = 0
podobne,
sin 30° = √(1/4) = 1/2
hriech 45° = √(2/4) = 1/√2
hriech 60° = √(3/4) = √3/2
hriech 90° = √(4/4) = 1

bez 0°	bez 30°	bez 45°	bez 60°	bez 90°
0	1/2	1/√2	√3/2	1

Krok 3: Vyhodnoťte hodnotu pre všetky uhly funkcie cos

Hodnota funkcie cos je opakom hodnoty funkcie sin t.j. cos 0° = sin 90°, cos 30° = sin 60° a cos 45° = sin 45°, takže

cos 0°	čo je 30°	čo je 45°	čo je 60°	čo je 90°
1	√3/2	1/√2	1/2	0

Krok 4: Vyhodnoťte hodnotu pre všetky uhly funkcie opálenia

Hodnota funkcie tan sa rovná funkcii sin delenej funkciou cos, t.j. tan x = sin x / cos x. Hodnota všetkých uhlov vo funkcii tan sa vypočíta ako,

tan 0°= sin 0° / cos 0° = 0/1 = 0, podobne

takže 0°	tak 30°	tak 45°	tak 60°	takže 90°
0	1/√3	1	√3	Neurčené

Krok 5: Vyhodnoťte hodnotu pre všetky uhly funkcie cosec

konverzia dátumu na reťazec

Hodnota funkcie cosec sa rovná prevrátenej hodnote funkcie sin. Hodnota cosec 0° sa získa zobratím prevrátenej hodnoty sin 0°

cosec 0° = 1 / sin 0° = 1 / 0 = nedefinované. podobne,

cosec 0°	cosec 30°	cosec 45°	cosec 60°	cosec 90°
Neurčené	2	√2	23	1

Krok 6: Vyhodnoťte hodnotu pre všetky uhly funkcie sek

Hodnota funkcie sec sa rovná recipročnej hodnote funkcie cos. Hodnota sek 0° sa získa zobratím prevrátenej hodnoty cos 0°

0° sek. = 1 / cos 0° = 1 / 1 = 1. Podobne

sek 0°	sek 30°	sek 45°	sek 60°	sek 90°
1	23	√2	2	Neurčené

Krok 7: Vyhodnoťte hodnotu pre všetky uhly funkcie postieľky

Hodnota funkcie detskej postieľky sa rovná prevrátenej hodnote funkcie tan. Hodnota detskej postieľky 0° sa získa ako prevrátená hodnota tan 0°

detská postieľka 0° = 1 /pálenie 0° = 1 / 0 = nedefinované. podobne,

postieľka 0°	postieľka 30°	postieľka 45°	postieľka 60°	postieľka 90°
Neurčené	√3	1	1/√3	0

Týmto spôsobom môžeme vytvoriť nasledujúcu tabuľku trigonometrických pomerov:

Trigonometrická tabuľka stupňov a radiánov
Uhol (v stupňoch)	Uhol (v radiánoch)	Bez	Cos	Takže	Cosec	Sek	Detská postieľka
0°	0	0	1	0	Nedefinované	1	Nedefinované
30°	p/6	1/2	√3/2	1/√3	2	23	√3
45°	p/4	√2/2	√2/2	1	√2	√2	1
60°	p/3	√3/2	1/2	√3	23	2	1/√3
90°	p/2	1	0	Nedefinované	1	Nedefinované	0

Trigonometrické vzorce

Dozvieme sa o niektorých trigonometrických vzorcoch súvisiacich s doplnkovými a doplnkovými uhlami.

Doplnkové uhly: Dvojica uhlov, ktorých súčet sa rovná 90°

Doplnkové uhly: Dvojica uhlov, ktorých súčet sa rovná 180°

Skontrolujte: Trigonometrické pomery

Trig Identity komplementárnych uhlov

Identity komplementárnych uhlov sú založené na vzťahu medzi goniometrickými funkciami dvoch uhlov, ktorých súčet dosahuje 90 stupňov (alebo π/2 radiánov). Tieto sú známe ako kofunkčné identity .

Goniometrická funkcia	Identita
Jeho	hriech (90°- i )=cos i
Kosínus	cos (90°- i )=bez i
Tangenta	opálená (90°- i )=postieľka i
Kotangens	detská postieľka (90°- i )=tak i
Secant	sek (90°- i )=csc i
Cosecant	cosec(90°- i )=sek i

Trig Identity doplnkových uhlov

Identity doplnkových uhlov sa týkajú goniometrických funkcií dvoch uhlov, ktorých súčet je 180 stupňov (alebo π radiánov).

Goniometrická funkcia	Identita
Jeho	hriech (180°- i )=bez i
Kosínus	cos (180°- i )=−cos i
Tangenta	opálená (180°- i )=−tan i
Kotangens	detská postieľka (180°- i )=−postieľka i
Secant	sek(180°- i )=−sek i
Cosecant	cosec(180°- i )=cosec i

Tabuľka goniometrických identít

Trigonometrické identity sú identity, ktoré sa vo veľkej miere používajú pri riešení goniometrických problémov. Existujú rôzne trigonometrické identity, ale tri hlavné trigonometrické identity sú:

Tabuľka trigonometrických identít
Trigonometrická identita	Vzorec
Pytagorova identita	bez²θ + cos²θ = 1
Sekant-tangentová identita	sek²θ – teda²θ = 1
Kosekant-kotangentová identita	cosec²θ – detská postieľka²θ = 1

Skontrolujte tiež:

Trigonometrické pomery

Inverzné goniometrické identity

Výšky a vzdialenosti

Príklady trigonometrickej tabuľky

Poďme vyriešiť niekoľko otázok na trigonometrickej tabuľke.

Príklad 1: Ak sin θ = 4/5, nájdite všetky trigonometrické hodnoty.

Riešenie:

Tu máme,

sin θ = 4/5
virtuálna pamäť

as, sin θ = kolmica / prepona

takže máme kolmicu (P) = 4 a preponu (H) = 5

Takže podľa Pythagorovej vety H ² = P ² +B ²

Poďme zistiť hodnotu základu (B)

5²= B²+ 4²
25 = B²+ 16
25-16 = B²
B²= 9
B = 3

Teraz máme,

Sin θ = kolmica/hypotenza
= AB/AC = 4/5

Kosínus θ = báza/hypotenza
= BC/AC = 3/5

Tangenta θ = kolmica/základňa
= AB/BC = 4/3

Kosekans θ = prepona/kolmica
= AC/AB = 5/4

Sekanta θ = prepona/základňa
= AC/BC = 5/3

Kotangens θ = základňa/kolmica
= BC/AB = 3/4

Príklad 2: Nájdite hodnotu cos 45° + 2 sin 60° – tan 60°.

Riešenie:

Z trigonometrickej tabuľky

cos 45° = 1/√2, sin 60° = √3/2 a tan 60° = √3

teda

cos 45° + 2 sin 60° – tan 60° = 1/√2 + 2(√3/2) – √3
= 1/√2

Príklad 3: Nájdite hodnotu cos 75°.

Riešenie:

My to vieme,

cos 75° = cos (45° + 30°) {as, cos (A + B) = cos A cos B – sin A sin B}
= cos 45° cos 30° – sin 45° sin 30°
= 1/√2 × √3/2 – 1/√2 × 1/2
= (√3 – 1)/2√2

cos 75°= (√3 – 1)/2√2.

Záver – Trigonometrická tabuľka

Trigonometrická tabuľka poskytuje komplexný odkaz na goniometrické funkcie sínus, kosínus, tangens, kosekans, sekans a kotangens spolu s ich príslušnými hodnotami pre rôzne uhly. ja t slúži ako cenný nástroj na riešenie goniometrické rovnice, analyzovanie geometrických vzťahov a pochopenie správania periodických javov. Či už v matematika, fyzika, inžinierstvo alebo iné oblasti, tabuľka trigonometrie pomáha pri výpočtoch, riešení problémov a vizualizácii, čím prispieva k hlbšiemu pochopeniu trigonometrických konceptov a ich aplikácií v scenároch reálneho sveta.