Uhol sa meria v stupňoch (°) a radiánoch. Je vytvorený medzi dvoma susednými stranami mnohouholníka. Každý mnohouholník má rôzne strany a rôzny počet uhlov. Vzorec na nájdenie uhlov v stupňoch je užitočný v geometrii a trigonometrii. Je nevyhnutné porozumieť iným pojmom matematiky, ako je oblúk, stredový uhol kruhu atď.
- Celý kruh = 360°
- Priamka = 180°
- Polkruh = 180°
- A Štvrťkruh = 90°
Výpočet uhlov v stupňoch
Existujú tri rôzne spôsoby hľadania uhlov v stupňoch, ktoré sú nasledovné:
- Použitie chrániča D
- Použitie Pythagorovej vety a trigonometrickej funkcie v pravouhlom trojuholníku
- Použitie vzorca súčtu uhlov
- Stredový uhol kruhu
Použitie chrániča D
Chránič je typ pravítka alebo stupnice, ktorá sa používa na meranie vzdialenosti v centimetroch alebo milimetroch. Chránič používaný na meranie uhlov má tvar „D“ s hodnotou uhlov označených od 0 do 180° z oboch smerov (sprava alebo zľava). Na meranie uhla musíme zarovnať os s čiarou na D. Stredný kruh chrániča je zarovnaný s vrcholom meraného uhla. Lúče pozdĺž vrcholu uhla pomôžu nájsť uhol v stupňoch.
Použitie Pytagorovej vety a trigonometrie v pravouhlom trojuholníku
V trigonometrii existuje šesť funkcií, sinus, cos, cosec, tan, postieľka, a sek. Pravouhlý trojuholník má tri strany, základňu, kolmicu a preponu.
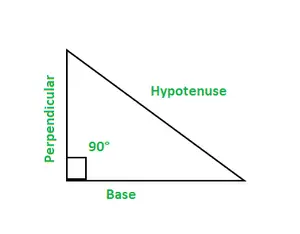
- Základňa: Je to priľahlá strana k uhlu 90°. Kolmica: Je tiež priľahlá strana k uhlu 90°. Prepona: Je to strana opačná k uhlu 90°.
Pravouhlý trojuholník predstavuje uhol 90° ako jeden z uhlov. Celkový súčet uhlov trojuholníka je 180°.
- Cosecθ: Predstavuje sa ako prepona delená kolmicou.
Cosecθ =
- Cotθ: Je znázornená ako základňa delená kolmicou.
Detská postieľkaθ =
Ostatné goniometrické funkcie sú reprezentované ako:
sinθ =
Cosθ =
tanθ =
sekθ =
Cosecθ môže byť tiež reprezentovaný ako 1/ sinθ
secθ môže byť tiež reprezentované ako 1/ cosθ
Cotθ môže byť tiež reprezentované ako 1/ tanθ
Kde,
Θ je uhol
Pythagorova veta
Ak sú známe dve strany pravého uhla, môžeme ľahko vypočítať tretiu stranu pravouhlého trojuholníka. V pravouhlom trojuholníku je Pytagorova veta daná takto:
(hypotenza)2= (základ)2+ (kolmo)2
Vzorec súčtu uhlov
Súčet uhlov sa vzťahuje na celkový súčet vnútorných uhlov mnohouholníka tvoriaceho sa medzi dvoma stranami. Ak existuje šesť strán mnohouholníka, existuje približne šesť uhlov. Pomáha nájsť uhol, ak sú známe iné uhly a súčet uhlov mnohouholníka.
Vzorec na nájdenie celkového súčtu uhlov mnohouholníka je daný:
Celkový súčet uhlov = 180 (n – 2)
Kde,
n je počet strán mnohouholníka
Príklad:
- Ak n = 4,

Celkový súčet uhlov = 180 (4 – 2)
= 180 (2)
= 360°
Ak n = 5,
Celkový súčet uhlov = 180 (5 – 2)
zásobník java= 180 (3)
= 540°
- Ak n = 6

Celkový súčet uhlov = 180 (6 – 2)
= 180 (4)
= 720°
Stredový uhol kruhu
Kruh je obrazec okrúhleho tvaru, ktorého hranica je rovnako vzdialená od jeho stredu. Vzdialenosť medzi stredovým bodom a hranicou je známa ako polomer kruhu. Uhol, ktorý tvoria dva polomery kruhu, je známy ako stredový uhol. Hodnota stredového uhla kruhu leží medzi 0 a 360 stupňami.

Vzorec na výpočet stredového uhla kruhu je daný:
Dĺžka oblúka = 2πr × (θ/360)
Θ = 360L/2pr
Kde,
r je polomer kružnice
AB je oblúk
Theta je uhol v stupňoch.
L = Dĺžka oblúka
Ukážkové problémy
Otázka 1: Nájdite stredový uhol kruhu s polomerom 2 m s dĺžkou oblúka 4 m?
Riešenie :
Vzorec na výpočet stredového uhla kruhu je daný:
Θ = 360L/2pr
Kde,
r je polomer kružnice
Theta je uhol v stupňoch.
L = Dĺžka oblúka
Θ = Uhol v stupňoch
r = 2 m
L = 4 m
Θ = 360 × 4/2 × π × 2
Ø = 114,6°
Stredový uhol kruhu je teda 114,6°.
Otázka 2: Nájdite stredový uhol kruhu s polomerom 10 cm s dĺžkou oblúka 18 cm?
Riešenie :
Vzorec na výpočet stredového uhla kruhu je daný:
js dekódovanie base64Θ = 360L/2pr
Kde,
r je polomer kružnice
Theta je uhol v stupňoch.
relácia vypršalaL = Dĺžka oblúka
r = 10 cm
L = 18 cm
Θ = Uhol v stupňoch
Θ = 360 × 18 /2 × π × 10
Ø = 103,13°
Stredový uhol kruhu je teda 103,13°.
Otázka 3: Nájdite uhol rovnobežníka, ak ostatné tri uhly sú 80°, 95° a 105°?
Riešenie :
V rovnobežníku sú štyri strany s celkovým súčtom uhlov 360°.
Vzorec na nájdenie súčtu uhlov = 180 (n – 2)
Kde,
n je počet strán mnohouholníka
Tu, n = 4,
Celkový súčet uhlov = 180 (4 – 2)
= 180 (2)
= 360°
Celkový súčet = Uhol 1 + Uhol 2 + Uhol 3 + Uhol 4
360 = 80+ 95+ 105+ Uhol 4
360 = 280 + Uhol 4
Uhol 4 = 360 – 280
Uhol 4 = 80°
Otázka 4: Nájdite uhol A na danom obrázku.

Riešenie :
Dané: prepona = 12
Kolmá = 6
Trigonometrická funkcia na výpočet uhla je daná vzťahom:
sinA = 6/12
A = 30°
Otázka 5: Nájdite uhol A na danom obrázku.

Riešenie :
Dané: prepona = 10
Základ = 5
Trigonometrická funkcia na výpočet uhla je daná vzťahom:
CosA = 5/10
A = 60°
Otázka 6: Nájdite uhol päťuholníka, ak ostatné štyri uhly sú 115°, 100°, 105° a 100°?
Riešenie :
Päťuholník má päť strán s celkovým súčtom uhlov 540°.
Vzorec na nájdenie súčtu uhlov = 180 (n – 2)
pole v jazyku JavaKde,
n je počet strán mnohouholníka
Tu, n = 5,
Celkový súčet uhlov = 180 (5 – 2)
= 180 (3)
= 540°
Celkový súčet = Uhol 1 + Uhol 2 + Uhol 3 + Uhol 4 + Uhol 5
540 = 115° + 100° + 105° + 100° + Uhol 5
540 = 420 + Uhol 5
Uhol 5 = 540 – 420
Uhol 5 = 120°
Otázka 7: Nájdite uhol A na danom obrázku.

Riešenie :
Dané: Základ = √3
Kolmá = 1
Trigonometrická funkcia na výpočet uhla je daná vzťahom:
tanθ =
tanθ = 1/√3
A = 30°
Otázka 8: Nájdite uhol rovnobežníka, ak ostatné tri uhly sú 100°, 70° a 80°?
Riešenie :
V rovnobežníku sú štyri strany s celkovým súčtom uhlov 360°.
Vzorec na nájdenie súčtu uhlov = 180 (n – 2)
Kde,
n je počet strán mnohouholníka
Tu, n = 4,
Celkový súčet uhlov = 180 (4 – 2)
= 180 (2)
= 360°
Celkový súčet = Uhol 1 + Uhol 2 + Uhol 3 + Uhol 4
360 = 100 + 70 + 80 + Uhol 4
360 = 250 + Uhol 4
Uhol 4 = 360 – 250
Uhol 4 = 110°
Ďalší uhol je teda 110°.
Otázka 9: Nájdite uhol šesťuholníka, ak je ďalších päť uhlov 120°, 115°, 110°, 125° a 105°?
čo je počítač
Riešenie :
V šesťuholníku je šesť strán s celkovým súčtom uhlov 720°.
Vzorec na nájdenie súčtu uhlov = 180 (6 – 2)
Kde,
n je počet strán mnohouholníka
Tu, n = 6,
Celkový súčet uhlov = 180 (6 – 2)
= 180 (4)
= 720°
Celkový súčet = Uhol 1 + Uhol 2 + Uhol 3 + Uhol 4 + Uhol 5 + Uhol 6
720 = 120 + 115 + 110 + 125 + 105 + Uhol 6
720 = 575 + Uhol 6
Uhol 6 = 720 – 575
Uhol 6 = 145°
Šiesty uhol šesťuholníka je teda 145°.






