Komplexné čísla sú prirodzeným pokračovaním reálnych čísel. V modernom veku sa komplexné čísla používajú v mnohých oblastiach, ako je digitálne spracovanie signálov, kryptografia a mnoho oblastí súvisiacich s počítačom.

V tomto článku sa dozvieme o imaginárnych číslach, komplexných číslach a ich type, rôznych operáciách s komplexnými číslami, vlastnostiach komplexných čísel, aplikácii komplexných čísel atď.

Definícia komplexných čísel

Komplexné čísla sú čísla formulára (a + i b) kde a & b sú skutočné čísla a i je imaginárna jednotka nazývaná iota, ktorá predstavuje √-1. Napríklad 2 + 3i je komplexné číslo, v ktorom 2 je reálne číslo a 3i je imaginárne číslo. Komplexné čísla možno zapísať ako a + ib, kde a a b sú racionálne čísla, ktoré možno znázorniť na číselnej osi siahajúcej až nekonečno .

Modul komplexného čísla

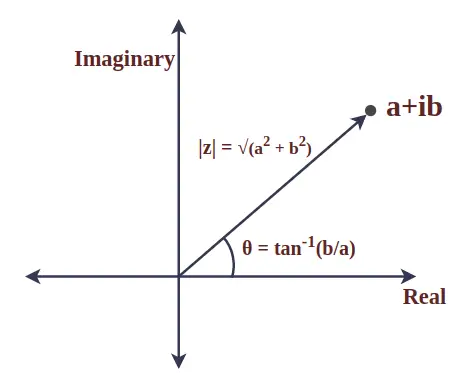
Modul komplexného čísla je absolútna hodnota a predstavuje vzdialenosť medzi počiatkom a daným bodom. Je tiež známy ako veľkosť komplexného čísla. Uvažujme komplexné číslo z = a + ib, potom je modul z definovaný ako:

premenná java

|z| = √(a ² + b ² )

kde,

• a je reálna časť komplexného čísla z, a
• b je imaginárna časť komplexného čísla z.

Argument komplexného čísla

Uhol medzi vektorom polomeru komplexného čísla a kladnou osou x sa nazýva argument komplexného čísla. Pre komplexné číslo z = a + ib je matematicky dané:

θ = tan ^-1 (b/a)

kde,

• a je reálna časť komplexného čísla z, a
• b je imaginárna časť komplexného čísla z.

Sila i(iota)

i(iota) je definovaná ako druhá odmocnina z -1. Akákoľvek mocnina i môže byť teda vyjadrená ako opakované násobenie i samo sebou, t.j.

• i = √ (-1)
• i²= -1
• i³= – i
• i⁴= 1
• i⁵= i
• i⁶= – 1
• a tak ďalej..

Potreba komplexných čísel

V staroveku ľudia poznali iba prirodzené čísla ako tieto čísla sú svojou povahou najintuitívnejšie, pretože ľudský mozog im už rozumie pomocou vizuálnych prvkov vecí, ako sú ovce a jedlo. Máme teda iba množinu prirodzených čísel ( N ), ale v prirodzených číslach neexistuje riešenie rovnice x + a = b (a> b) a a, b ∈ N. Vzniklo teda rozšírenie prirodzených čísel, t. j. celé čísla ( ja ).

Teraz opäť v tejto množine čísel neexistuje riešenie rovnice, ax = b (a ≠ 0) a a, b ∈ I, kde a aj b sú celé čísla. Množina celých čísel (I) je teda rozšírená na množinu racionálnych čísel ( Q ).

V tejto množine racionálnych čísel opäť neexistuje riešenie rovnice x²= a (a> 0) a a ∈ Q. Teda Q sa rozšíri o čísla také, že x²= a(pre a> 0) t.j. iracionálne čísla. Táto množina sa nazýva skutočné čísla a predstavuje ju R .

Teraz sa dlho myslelo, že túto množinu reálnych čísel nemusíme rozširovať, aby sme vytvorili ďalšiu väčšiu množinu, pretože táto zbierka čísel sa zdá byť kompletná. Ale opäť sa v tejto množine čísel objavil nový problém, t. j. neexistuje žiadne reálne číslo také, že x²= a (a <0) a a ∈ R. Množina reálnych čísel sa teda ďalej rozširuje, aby zahŕňala všetky takto hodnotené a pomenované komplexné čísla a je reprezentovaná C .

Klasifikácia komplexných čísel

Ako vieme, štandardný tvar komplexného čísla je z = (a + i b) kde a, b ∈ R, a i je iota (imaginárna jednotka). Takže v závislosti od hodnôt a (nazývaná reálna časť) a b (nazývaná imaginárna časť) sú komplexné čísla rozdelené do štyroch typov:

• Nulové komplexné číslo
• Čisto reálne čísla
• Čisto vymyslené čísla
• Imaginárne čísla

Poďme sa o týchto typoch dozvedieť podrobnejšie.

Nulové komplexné číslo

Pre akékoľvek komplexné číslo z = a + ib, ak a = 0 & b = 0, komplexné číslo sa nazýva nulové komplexné číslo. Napríklad jediným príkladom je 0.

Čisto reálne čísla

Pre akékoľvek komplexné číslo z = a + ib, ak a ≠ 0 & b = 0, sa komplexné číslo nazýva čisto reálne číslo, t. j. číslo bez imaginárnej časti. Všetky reálne čísla sú príkladmi toho, že 2, 3, 5, 7 atď.

Čisto vymyslené čísla

Pre akékoľvek komplexné číslo z = a + ib, ak a = 0 & b ≠ 0, sa komplexné číslo nazýva čisto imaginárne číslo, t. j. číslo bez reálnej časti. Všetky čísla bez reálnych častí sú príkladmi tohto typu čísel, t. j. -7i, -5i, -i, i, 5i, 7i atď.

Imaginárne čísla

Pre akékoľvek komplexné číslo z = a + ib, ak a ≠ 0 & b ≠ 0, sa komplexné číslo nazýva imaginárne číslo . Napríklad (-1 – i), (1 + i), (1 – i), (2 + 3i) atď.

Rôzne formy komplexných čísel

Existujú rôzne formy komplexných čísel,

• Obdĺžnikový tvar
• Polárna forma
• Exponenciálna forma

Teraz sa o nich dozvieme podrobne.

Obdĺžnikový tvar

Obdĺžnikový tvar je tiež nazývaný Štandardná forma a zastupuje ho (a + ib), kde a a b sú reálne čísla.

Napríklad: (5 + 5i), (-7i), (-3 – 4i) atď.

Polárna forma

Polárna forma je znázornenie komplexného čísla, kde polárne súradnice [kde súradnice sú vyjadrené ako (r, θ), kde r je vzdialenosť od začiatku a θ je uhol medzi čiarou spájajúcou bod a počiatok a kladnou osou x) sa používajú na vyjadrenie komplexného čísla. Akékoľvek komplexné číslo je reprezentované ako r [cos θ + i sin θ].

Napríklad: [cos π/2 + i sin π/2], 5[cos π/6 + i sin π/6] atď.

Exponenciálna forma

Exponenciálne tvary komplexných čísel je reprezentácia komplexných čísel pomocou Eulerovho vzorca a v tejto forme je komplexné číslo reprezentované reⁱ, kde r je vzdialenosť bodu od začiatku a θ je uhol medzi kladnou osou x a vektorom polomeru.

Napríklad: eⁱ⁽⁰⁾, To je^i(π/2), 5.e^i(π/6), atď.

Poznámka: Všetky tri formy komplexných čísel diskutované vyššie sú vzájomne konvertibilné, t. j. môžu sa veľmi ľahko previesť z jednej formy do druhej.

Operácie s komplexnými číslami

S komplexnými číslami je možné vykonávať nasledujúce operácie:

• Doplnenie
• Odčítanie
• Násobenie
• divízie
• Konjugácia

Sčítanie komplexných čísel

Môžeme sčítať dve komplexné čísla jednoduchým sčítaním ich skutočných a imaginárnych častí oddelene.

Napríklad (3 + 2i) + (1 + 4i) = 4 + 6i.

Odčítanie komplexných čísel

Môžeme odčítať dve komplexné čísla jednoduchým odčítaním ich skutočných a imaginárnych častí oddelene.

Napríklad (3 + 2i) – (1 + 4i) = 2 – 2i.

java pole na zoznam

Násobenie komplexných čísel

Dve komplexné čísla môžeme vynásobiť pomocou distributívnej vlastnosti a skutočnosti, že i²= -1.

Napríklad (3 + 2i)(1 + 4i) = 3 + 12i + 2i + 8i²= 3 + 14i – 8 = -5 + 14i.

Delenie komplexných čísel

Jedno komplexné číslo môžeme deliť druhým jednoduchým vynásobením čitateľa aj menovateľa komplexným konjugátom menovateľa a ďalším zjednodušením výrazu.

Napríklad (3 + 2i)/(1 + 4i) = (3 + 2i)(1 – 4i)/(1 + 4i)(1 – 4i) = (11 – 10i)/17.

Konjugácia komplexných čísel

Môžeme ľahko nájsť konjugát komplexného čísla, jednoduchou zmenou znamienka jeho pomyselnej časti. Konjugát komplexného čísla sa často označuje čiarou nad číslom, napríklad z̄.

Napríklad konjugát 3 + 2i je 3 – 2i.

Identity pre komplexné čísla

Pre ľubovoľné dve komplexné čísla z₁a z₂môžu byť dané nasledujúce algebraické identity:

• (S ₁ + z ₂ ) ² = (z ₁ ) ² + (z ₂ ) ² + 2 z ₁ × z ₂
• (S ₁ - S ₂ ) ² = (z ₁ ) ² + (z ₂ ) ² – 2 z ₁ × z ₂
• (S ₁ ) ² - (s ₂ ) ² = (z ₁ + z ₂ ) (s ₁ - S ₂ )
• (S ₁ + z ₂ ) ³ = (z ₁ ) ³ + 3 (z ₁ ) ² S ₂ +3(z ₂ ) ² S ₁ + (z ₂ ) ³
• (S ₁ - S ₂ ) ³ = (z ₁ ) ³ – 3 (z ₁ ) ² S ₂ +3(z ₂ ) ² S ₁ - (s ₂ ) ³

Vzorce súvisiace s komplexnými číslami

Existuje niekoľko vzorcov súvisiacich s komplexnými číslami, z ktorých niektoré sú nasledovné:

Eulerov vzorec

Eulerov vzorec ukazuje vzťah medzi imaginárnou mocnosťou exponentu a trigonometrického pomeru sin a cos a je daný vzťahom:

to je ^ix = cos x + i sin x

De Moivreov vzorec

De Moivreov vzorec vyjadruje n^thmocnina komplexného čísla v polárnom tvare a je daná vzťahom:

(cos x + ja hriech x) ⁿ = cos(nx) + i sin(nx)

Komplexná rovina

Rovina, na ktorej sú komplexné čísla jednoznačne zastúpené, sa nazýva komplexná rovina alebo Argandova rovina alebo Gaussova rovina.

Komplexná rovina má dve osi:

• Os X alebo Skutočná os
• Y-os alebo imaginárna os

Os X alebo Skutočná os

• Všetky čisto reálne komplexné čísla sú jednoznačne reprezentované bodkou.
• Reálna časť Re(z) všetkých komplexných čísel je vynesená vzhľadom na ňu.
• Preto sa tiež nazýva os X Skutočná os .

Y-os alebo imaginárna os

• Všetky čisto imaginárne komplexné čísla sú jednoznačne reprezentované bodkou.
• Imaginárna časť Im(z) všetkých komplexných čísel je vynesená vzhľadom na ňu.
• Preto sa os Y tiež nazýva Pomyselná os .

Geometrické zobrazenie komplexných čísel

Ako vieme, každé komplexné číslo (z = a + i b) je reprezentované jedinečným bodom p(a, b) v komplexnej rovine a každý bod v komplexnej rovine predstavuje jedinečné komplexné číslo.

Ak chcete reprezentovať akékoľvek komplexné číslo z = (a + i b) v komplexnej rovine, postupujte podľa týchto konvencií:

• Reálna časť z (Re(z) = a) sa stáva X-ovou súradnicou bodu p

• Imaginárna časť z (Im(z) = b) sa stáva Y-ovou súradnicou bodu p

A nakoniec z (a + i b) ⇒ p (a, b), čo je bod v komplexnej rovine.

Vlastnosti komplexných čísel

Komplexné čísla majú rôzne vlastnosti, z ktorých niektoré sú nasledovné:

• Pre akékoľvek komplexné číslo z = a + ib, ak z = 0, potom a = 0, ako aj b = 0.
• Pre 4 reálne čísla a, b, c a d také, že z₁= a + ib a z₂= c + id. Ak z₁= z₂potom a = c a b = d.
• Sčítanie komplexného čísla s jeho konjugátom vedie k čisto reálnemu číslu, t. j. z + z̄ = reálne číslo.

Nech z = a + ib,

z + z̄ = a + jedna + a – jedna

⇒ z + z̄ = 2a (čo je čisto skutočné)

• Súčin komplexného čísla s jeho konjugovanými výsledkami je tiež čisto reálne číslo, t. j. z × z̄ = skutočné číslo

Nech z = a + ib

z × z̄ = (a + jedna) × (a – jedna)

⇒ z × z̄= a²– i²b²

⇒ z × z̄ = a²+ b²(čo je čisto skutočné)

• Komplexné čísla sú komutatívny pri operácii sčítania a násobenia. Uvažujme dve komplexné čísla z₁a z₂, a potom

S ₁ +z ₂ = z ₂ +z ₁

S ₁ × z ₂ = z ₂ × z ₁

• Komplexné čísla sú asociatívne s operáciou sčítania a násobenia. Uvažujme tri komplexné čísla z₁, S₂, a z₃potom

(S ₁ +z ₂ ) +z ₃ = z ₁ + (z ₂ +z ₃ )

(S ₁ ×z ₂ )×z ₃ = z ₁ ×(z ₂ ×z ₃ )

• Komplexné čísla držia distribučný majetok násobenia nad sčítaním rovnako. Uvažujme tri komplexné čísla z₁, S₂, a z₃potom

S ₁ ×(z ₂ +z ₃ ) = z ₁ ×z ₂ + z ₁ ×z ₃

Čítaj viac,

• Delenie komplexných čísel
• Z Bar v komplexných číslach

Príklady komplexných čísel

Príklad 1: Zostrojte tieto komplexné čísla z = 3 + 2i v komplexnej rovine.

Riešenie:

Vzhľadom na to:

S = 3 + 2 i

Takže bod je z(3, 2). Teraz vynesieme tento bod do nižšie uvedeného grafu, tu v tomto grafe os x predstavuje skutočnú časť a os y predstavuje imaginárnu časť.

Príklad 2: Zostrojte tieto komplexné čísla z ₁ = (2 + 2 i), z ₂ = (-2 + 3 i), z ₃ = (-1 – 3 i), z ₄ = (1 – i) v komplexnej rovine.

Riešenie:

Vzhľadom na to:

S₁= (2 + 2 i)

S₂= (-2 + 3 i)

S₃= (-1 – 3 i)

S₄= (1 – i)

Body sú teda z₁(2, 2), z₂(-2, 3), z₃(-1, -3) a z₄(1, -1). Teraz vynesieme tieto body do nižšie uvedeného grafu, tu v tomto grafe os x predstavuje skutočnú časť a os y predstavuje imaginárnu časť.

Časté otázky o komplexných číslach

Definujte komplexné čísla.

Čísla v tvare a+ib sa nazývajú komplexné číslo, kde aab sú reálne čísla a i je imaginárna jednotka, ktorá predstavuje druhú odmocninu z -1.

Aký je rozdiel medzi skutočným číslom a komplexným číslom?

Rozdiel medzi reálnymi a komplexnými číslami je v tom, že na reprezentáciu akéhokoľvek reálneho čísla potrebujeme iba jedno číslo, ale na reprezentáciu akéhokoľvek komplexného čísla potrebujeme dve reálne čísla.

Aká je skutočná a imaginárna časť komplexného čísla?

V komplexnom čísle a + ib je a reálna časť komplexného čísla a b sa nazýva imaginárna časť komplexného čísla.

Čo je komplexný konjugát komplexného čísla?

Pre komplexné číslo a + ib sa a – ib nazýva jeho komplexný konjugát. Komplexné konjugáty možno nájsť jednoduchou zmenou znamienka imaginárnej časti.

Aký je modul komplexného čísla?

Vzdialenosť medzi počiatkom a bodom reprezentovaným komplexným číslom v argandovej rovine sa nazýva modul tohto úplného čísla a pre z = a + ib je matematicky daná:

|z| = √(a ² + b ² )

rovná sa metóda java

Aký je argument komplexného čísla?

Uhol medzi vektorom polomeru komplexného čísla a kladnou osou x sa nazýva argument komplexného čísla a pre z = a + ib je matematicky daný:

θ = tan ^-1 (b/a)

Aký je polárny tvar komplexného čísla?

Pre akékoľvek komplexné číslo, z = a + ib, je jeho polárna forma daná vzťahom:

r [cos θ + i sin θ]

Aký je Eulerov vzorec?

Eulerov vzorec ukazuje vzťah medzi imaginárnou mocnosťou exponentu a trigonometrického pomeru sin a cos a je daný vzťahom:

to je ^ix = cos x + i sin x