logo

TechCodeview

Plošné vzorce

Plošné vzorce pre rôzne objekty sú vzorce, ktoré sa používajú na nájdenie oblasti rôznych objektov. Plocha je priestor, ktorý zaberá hranica ľubovoľnej postavy. Plošné vzorce rôznych geometrických tvarov závisia od rôznych parametrov, ako sú rozmery, výška a polomer rôznych geometrických tvarov. Geometrické tvary sú dvoch typov:

  • Dvojrozmerné tvary (2-D tvary)
  • Trojrozmerné tvary (3-D tvary)

V tomto článku sa budeme podrobne učiť o plošných vzorcoch pre rôzne 2-D a 3-D tvary, ako je plocha obdĺžnika, plocha štvorca, plocha kruhu, plocha kocky atď. a iné.



Obsah

Čo je oblasť?

Priestor, ktorý zaberá hranica obrazca, sa nazýva plocha obrazca. Meria sa v jednotkách štvorcových. Jednotkou SI na meranie plochy je m2. Oblasť sa používa v rôznych matematických konceptoch a používa sa aj v scenároch skutočného života, ako je napríklad nájdenie oblasti miestnosti, tabuľky oblastí atď.

Čo sú plošné vzorce?

Plošné vzorce sú základné nástroje používané v matematike na výpočet množstva priestoru uzavretého rôznymi dvojrozmernými tvarmi. Tieto vzorce možno použiť na nájdenie geometrickej oblasti postavy, ako sú štvorce, obdĺžniky, kruhy, trojuholníky, lichobežníky a elipsy. Pomocou týchto vzorcov môžeme presne vypočítať plochu rôznych tvarov, čo nám umožňuje riešiť problémy v reálnom svete a robiť dôležité výpočty.



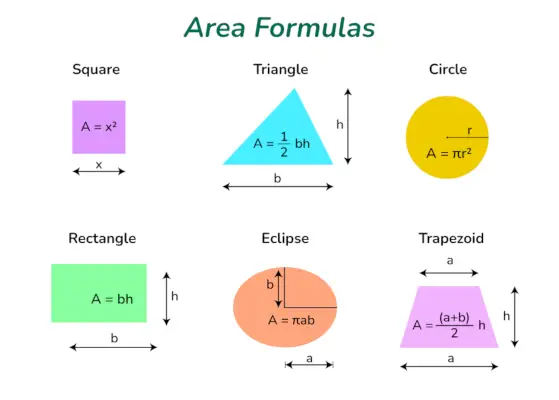
Oblasť-vzorce

Plošné vzorce

Čo sú 2D tvary?

Tvary, ktoré majú iba dva rozmery, sa nazývajú 2-D tvary . Sú nakreslené v 2-D priestore a sú závislé na 2 parametre, všeobecne dĺžka(l) a šírka(b). Rôzne 2-D tvary sú, Obdĺžnik, Štvorec, Trojuholník, Kruhy a iné.

Vzorec oblasti 2D tvarov

Vzorce pre oblasť 2D tvarov sú vzorce, ktoré sa používajú na zobrazenie plochy rôznych 2D tvarov, ako je plocha trojuholníka, plocha štvorca, plocha obdĺžnika, plocha kosoštvorca atď. Tieto plošné vzorce sa v matematike veľmi používajú na riešiť rôzne geometrické úlohy. Rôzne plošné vzorce pre rôzne tvary sú,



Plošný vzorec obdĺžnika

Obdĺžnik je 2-rozmerná postava ktorý je štvoruholník, teda má štyri strany jeho protiľahlé strany sú rovnobežné a rovnaké. Všetky uhly v obdĺžniku sú rovnaké a ich miera je 90 stupňov. Uhlopriečky obdĺžnika sú rovnaké a sú navzájom kolmými stredmi.

Vzorec na výpočet plochy obdĺžnika je s dĺžkou a l a šírku b je,

  • Plocha obdĺžnika (A) = l×b štvorcových jednotiek

Plošný vzorec štvorca

Štvorec je 2-rozmerný obrazec, ktorý je štvoruholníkom, t.j. má štyri strany, protiľahlé strany sú rovnobežné a všetky štyri strany štvorca sú rovnaké. Všetky uhly v štvorci sú rovnaké a ich miera je 90 stupňov. Uhlopriečky štvorca sú rovnaké a sú navzájom kolmými osami.

Vzorec na výpočet plochy štvorca so stranou a je,

  • Plocha štvorca (A) = a 2 štvorcových jednotiek

Plošný vzorec trojuholníka

Trojuholník je najjednoduchší mnohouholník, ktorý vzniká spojením troch priamych čiar. Ako už názov napovedá, ide o polygón s tromi uhlami. Súčet dĺžok všetkých strán trojuholníka je obvod trojuholníka a priestor vo vnútri obvodu trojuholníka je obsah trojuholníka.

mvc v jarnom rámci

Vzorec na výpočet obsahu trojuholníka so základňou b je a výška h je,

  • Plocha trojuholníka (A) = 1/2 × bh štvorcových jednotiek

Plošný vzorec kruhu

Kruh je geometrický útvar bez priamej čiary. Je to ťažisko bodu, ktoré je vždy v konštantnej vzdialenosti od pevného bodu. Pevný bod sa nazýva stred kruhu a pevná vzdialenosť je polomer kruhu.

Vzorec na výpočet oblasť kruhu s r ako polomer kruhu,

  • Plocha kruhu (A) = πr 2 štvorcových jednotiek

Plošný vzorec rovnobežníka

Paralelogram je 2-D obrazec v ktorých sú protiľahlé strany rovnobežné a rovnaké. Vzorec na výpočet plochy rovnobežníka so základňou b a výška h sú,

  • Plocha rovnobežníka (A) = jednotky bh štvorcových

Plošný vzorec kosoštvorca

Rhombus je štvoruholník so všetkými štyrmi stranami rovnakými a rovnobežnými, ale nie všetky uhly sú rovnaké. Vzorec na výpočet plochy kosoštvorca s uhlopriečkou d 1 a d 2 sú,

  • Plocha kosoštvorca (A) = 1/2 × d 1 × d 2 štvorcových jednotiek

Plošný vzorec lichobežníka

Lichobežník je iný názov lichobežník . Je to štvoruholník, v ktorom sú protiľahlé strany rovnobežné. Vzorec na výpočet plochy lichobežníka s rovnobežnými stranami a a b a výška h je,

  • Plocha lichobežníka (A) = 1/2(a +b)h štvorcových jednotiek

Plošný vzorec elipsy

Elipsa má 2-D tvar a spadá pod kužeľové rezy. Vzorec na výpočet plochy elipsy s osou as a a b sú,

  • Plocha elipsy (A) = πab štvorcových jednotiek

Plošný vzorec polkruhu

Polkruh je 2-D postava, ktorá je polovicou kruhu. Vzorec na výpočet plochy polkruhu s polomerom r je,

  • Plocha polkruhu (A) = 1/4 (πr 2 ) štvorcových jednotiek

Tabuľka vzorcov oblasti

Vzorce pre oblasti rôznych 2-D obrázkov sú pridané do tabuľky pridanej nižšie,

Figúrky

Vzorec

Premenné

Obdĺžnik

Plocha = l×b
  • l je dĺžka
  • b je šírka

Námestie

Plocha = a2

a je strana štvorca

Trojuholník

Plocha = 1/2×bh
  • b je základ
  • h je výška

Kruh

Plocha = πr2

r je polomer kružnice

Lichobežník

Plocha = 1/2×(a+b)h
  • a je prvá základňa
  • b je druhá základňa

Rhombus

Plocha = 1/2 × d1×d2
  • d1je Jedna uhlopriečka
  • d2je druhá uhlopriečka

Paralelogram

Plocha = b × h
  • b je základ
  • h je výška

Elipsa

Plocha = πab
  • a je polomer hlavnej osi
  • b je polomer vedľajšej osi

Čo sú 3D tvary?

3-D tvary sú tvary, ktoré sú nakreslené v 3-D priestoroch. Majú 3 rozmery, ktoré sú ich parametrami. Plocha týchto tvarov závisí od dĺžky, šírky a výšky 3-D tvarov. Rôzne trojrozmerné tvary sú kocka, kváder, valec, kužeľ, guľa a iné. Plocha 3-D tvarov patrí do dvoch kategórií, ktorými sú zakrivená plocha (plocha bočného povrchu){CSA} a celková plocha povrchu (TSA). CSA je plocha všetkých zakrivených plôch 3-D tvarov a TSA je plocha všetkých plôch 3-D tvarov.

Vzorec oblasti 3D tvarov

Plocha 3-D tvarov je priestor, ktorý zaberajú všetky tváre postavy. Meria sa v jednotkách2. Jednotkou SI plochy je m2. The plocha kocky , plocha kvádra , plocha valca, plocha kužeľa a iné prichádza v oblasti 3D tvarov. Tabuľka pridaná nižšie ukazuje vzorce rôznych 3-D obrázkov.

Oblasť tvaru

Plocha povrchu

Parametre

Oblasť kocky

6a2

a je dĺžka okraja

Oblasť kvádra

2 (lb + lh + bh)
  • l je dĺžka okraja
  • b je šírka okraja
  • h je výška hrany

Oblasť kužeľa

πr(r + l)
  • r = polomer kruhovej základne
  • l = výška sklonu

Oblasť valca

2π(r + h)
  • r = polomer kruhovej základne
  • h = výška valca

Oblasť Sphere

4πr2

r je polomer gule

Oblasť hemisféry

3πr2

vypnutie režimu vývojára

r je polomer pologule

Oblasť pravouhlého hranola

2 (wl + hl + hw)
  • l je dĺžka okraja
  • w je šírka okraja
  • h je výška hrany

Tiež skontrolujte

  • Plošné a obvodové vzorce
  • Vzorce plochy povrchu

Príklady plošných vzorcov

Príklad 1: Nájdite plochu obdĺžnika s dĺžkou 5 cm a šírkou 2 cm.

Riešenie:

Vzhľadom na to,

  • Dĺžka obdĺžnika (l) = 5 cm
  • Šírka obdĺžnika (b) = 2 cm

Plocha obdĺžnika (A) = l × b

A = 5 cm × 2 cm
= 10 cm2

Príklad 2: Nájdite plochu štvorcového parku, ktorého strana je 4 m.

Riešenie:

Vzhľadom na to,

  • Strana štvorca (a) = 4 m

Plocha štvorca = a2
= (4)2= 16 m2

trieda objektov v jazyku Java

Plocha štvorcového parku je teda 16 m2

Príklad 3: Nájdite obsah trojuholníkovej dosky, ktorej výška je 6 cm a základňa je 6 cm.

Riešenie:

Vzhľadom na to,

  • Výška trojuholníka (v) = 6 cm
  • Základňa trojuholníka (b) = 8 cm

Plocha trojuholníka (A) = 1/2 (b × h)

A = 1/2 (8 × 6)
= 48/2 = 24 cm2

Plocha trojuholníkového taniera je 24 cm2

Príklad 4: Nájdite plochu kruhového disku s polomerom 1,4 cm.

Riešenie:

Vzhľadom na to,

  • Polomer kruhu (r) = 1,4 cm

Plocha kruhu (A) = πr2

A = π (1,4)2
= 22/7 (1,4) (1,4) = (4,4) (1,4)
= 6,16 cm2

Plocha kruhového kotúča je 6,16 cm2

Časté otázky týkajúce sa vzorcov oblasti

Čo sú plošné vzorce?

Plošné vzorce sú vzorce, ktoré sa používajú na nájdenie plochy ľubovoľného obrázku. Používa sa na zistenie množstva miesta, ktoré figúrka zaberá. Vo všeobecnosti je oblasť označená písmenom „A“. a meria sa v jednotkách2, t.j. cm2, m2, atď.

Čo je vzorec oblasti pre štvorec?

Plošný vzorec pre štvorec je vzorec na výpočet priestoru, ktorý štvorec zaberá. Vzorec na výpočet plochy štvorca je,

Plocha štvorca = (strana) 2

Čo je vzorec oblasti pre obdĺžnik?

Plošný vzorec pre obdĺžnik je vzorec na výpočet priestoru, ktorý obdĺžnik zaberá. Vzorec na výpočet plochy obdĺžnika je,

Plocha obdĺžnika = dĺžka × šírka

Čo je vzorec oblasti pre trojuholník?

Plošný vzorec pre trojuholník je vzorec na výpočet priestoru, ktorý trojuholník zaberá. Vzorec na výpočet plochy trojuholníka je,

Plocha trojuholníka = 1/2 (základňa × výška)

Čo je vzorec oblasti pre kruh?

Plošný vzorec pre kruh je vzorec na výpočet priestoru, ktorý zaberá kruh. Vzorec na výpočet plochy kruhu je,

Oblasť kruhu = π (polomer) 2

Čo je plošný vzorec pre štvoruholník?

Vzorec na výpočet plochy štvoruholníka,

Plocha štvoruholníka = 1/2 × uhlopriečka 1 × Uhlopriečka 2

Čo je plošný vzorec trojuholníkového hranola?

Vzorec pre oblasť trojuholníkového hranola je,

Plocha trojuholníkového hranola = (obvod základne × dĺžka hranola) + 2 × plocha základne

Čo je plošný vzorec mnohouholníka?

Vzorec na výpočet plochy mnohouholníka je,

Plocha mnohouholníka = 1/2 × (obvod × apotém)

Čo je plošný vzorec pravého trojuholníka?

Vzorec pre oblasť pravouhlého trojuholníka je,

Plocha pravého trojuholníka = 1/2 × kolmica × základňa

Čo je plošný vzorec Pentagonu?

Vzorec pre oblasť Pentagonu je,

Plocha Pentagonu = 1/2 × Obvod × Apotém