Trapéz v matematike: Lichobežník je mnohouholník so štyrmi stranami, t.j. je to štvoruholník. Trapezium vzniklo z gréckeho slova trapeze, čo znamená stôl. Je to zložitý štvoruholník. Lichobežník je špeciálny štvoruholník s iba jedným párom rovnobežných strán. Lichobežník je dvojrozmerný tvar, ktorý sa javí ako stôl.
Lichobežník má štyri strany a štyri vrcholy. Lichobežníkový tvar vidíme v našom každodennom živote a je to jeden z najbežnejších tvarov. V tomto článku sa dozvieme o čo je lichobežník v matematike, jeho vlastnosti, vzorce, príklady a typy lichobežníka, spolu s niektorými jeho vyriešenými príkladmi.
Obsah
inštancia java
- Čo je to lichobežník v matematike?
- Druhy lichobežníka
- Nepravidelný trapéz
- Vlastnosti lichobežníka
- Trapézium Formula
- Oblasť trapézového vzorca
- Obvod trapézového vzorca
- Rozdiel medzi lichobežníkom a lichobežníkom
- Trapézové uhly
- Uhlopriečka lichobežníka
- Príklady lichobežníka
Čo je to lichobežník v matematike?
Lichobežník je uzavretý dvojrozmerný štvoruholník, ktorý má pár rovnobežných protiľahlých strán. Rovnobežné strany lichobežníka sa nazývajú základne a nerovnobežné strany lichobežníka sa nazývajú nohy. Lichobežník má štyri strany a štyri rohy. A rovnobežník sa nazýva aj lichobežník s dvoma rovnobežnými stranami.
Definícia lichobežníka
Lichobežník je štvoruholník (štvorstranný mnohouholník) s aspoň jedným párom rovnobežných strán. Tieto rovnobežné strany sa označujú ako základy lichobežníka a ďalšie dve strany sa nazývajú nohy, ktoré nemusia byť nevyhnutne rovnobežné.
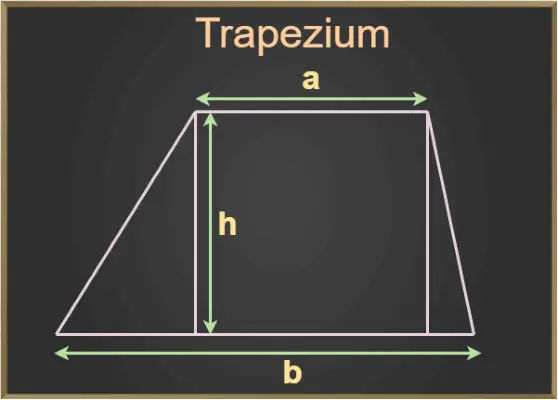
Na obrázku vyššie sú a a b základne lichobežníka a h je výška lichobežníka.
Tvar lichobežníka
Trapéz je a štvoruholník tj mnohouholník so štyrmi stranami. Lichobežník má štyri strany s párom protiľahlých strán navzájom rovnobežných. Lichobežníkový tvar je veľmi bežný a v každodennom živote vidíme rôzne veci, ktoré sú podobné lichobežníku. Niektoré nami pozorované príklady lichobežníka v reálnom živote sú stoly v tvare lichobežníka, dlaždice, obrazy a iné.
Druhy lichobežníka
Na základe strán a uhlov je lichobežník troch typov:
- Scalene Trapezium
- Rovnoramenný lichobežník
- Pravý trapéz

Rovnoramenný lichobežník
Lichobežník, ktorý má rovnakú dĺžku nôh, sa nazýva rovnoramenný lichobežník, t.j. v rovnoramennom lichobežníku sú dve nerovnobežné strany rovnaké.
Scalene Trapezium
Lichobežník, ktorého všetky strany nie sú rovnaké, sa nazýva scalene lichobežník. V skalnom lichobežníku nie sú žiadne dva uhly rovnaké.
Pravý trapéz
Lichobežník, ktorý má vedľa seba pravý uhlový pár, je známy ako pravý lichobežník.
Nepravidelný trapéz
Lichobežník má jeden pár rovnobežných strán a ostatné dve strany sú nerovnobežné. V pravidelnom lichobežníku sú ostatné dve nerovnobežné strany rovnaké, ale v prípade nepravidelného lichobežníka sú dve nerovnobežné protiľahlé strany nerovnaké.
Vlastnosti lichobežníka
Existujú rôzne vlastnosti lichobežníka, z ktorých niektoré sú nasledovné:
- Paralelné strany: Lichobežník má dve rovnobežné strany, ktoré sa nazývajú základne. Príklad: Strany AB a CD sú navzájom rovnobežné, ako je znázornené na obrázku.
- Neparalelné strany: Nerovnobežné strany lichobežníka sa nazývajú nohy a nohy lichobežníka nemajú rovnakú dĺžku. Príklad: Strany AD a BC sú nerovnobežné strany lichobežníka.
- Výška alebo nadmorská výška: Kolmá vzdialenosť medzi základňami sa nazýva výška alebo nadmorská výška lichobežníka. Vo vyššie uvedenom diagrame je h výška lichobežníka.
- Súčet uhlov
- Naklonené vnútorné uhly v lichobežníku dosahujú súčet až 180°. Príklad: Existujú dva páry vnútorných uhlov. Jeden pár je ∠ A a ∠ D, zatiaľ čo druhý pár je ∠ B a ∠ C. Súčet každej dvojice vnútorných uhlov je 180°.
- Súčet všetkých vnútorných uhlov v lichobežníku je vždy 360°. Príklad : Na obrázku ∠A+∠D je 180° a ∠B+∠C je 180°. Preto ∠A+∠D +∠B+∠C = 360°.
- Medián: Stred lichobežníka je úsečka, ktorá spája stredné body nôh. Medián je rovnobežný so základňami a jeho dĺžka je priemerom dĺžok základov.
- Lichobežník má presne jeden pár protiľahlých strán, ktoré sú rovnobežné.
Trapézium Formula
Dôležité vzorce lichobežníka sú:
- Oblasť Trapezium = ½ (súčet rovnobežných strán) × (vzdialenosť medzi rovnobežnými stranami)
- Obvod lichobežníka = Súčet všetkých štyroch strán
Oblasť trapézového vzorca
Lichobežník má dve rovnobežné strany a, respektíve b jednotky a jeho nadmorská výška je h.
Teraz je možné vypočítať plochu lichobežníka nájdením priemeru základní a vynásobením jeho výsledku nadmorskou výškou. teda
Oblasť Trapezium = ((a +b)/2) x h
kde,
- a a b sú Základy trapézu
- h je nadmorská výška
Oblasť rovnoramenného lichobežníka
Nech a a b sú dĺžky rovnobežných strán lichobežníka ABCD, kde a a b sú základne lichobežníka a a>b.
Teraz, keďže ide o rovnoramenný lichobežník, c je dĺžka oboch dvoch nerovnobežných strán a h je výška lichobežníka.
Teraz AB = a, CD = b, BC = AD = c
In Správny trojuholník , AED
Dĺžka kolmice, h = √(c 2 – (a-b) 2 ) [použitím Pythagorova veta ]….(1)
teraz
Plocha = ½ × súčet rovnobežných strán × výška lichobežníka
Plocha = ½ × (a+b) × h
Použitie rovnice (1)
Oblasť rovnoramenného lichobežníka = 1/2 × [√(c 2 – (a-b) 2 ) (a+b)]
Obvod trapézového vzorca
Obvod lichobežníka je daný výpočtom súčtu všetkých jeho strán. teda
Obvod lichobežníka = AB + BC + CD + AD
kde, AB, BC, CD a AD sú Strany lichobežníka
Obvod rovnoramenného lichobežníka
Ak v rovnoramennom lichobežníku a a b sú dĺžky rovnobežných strán, t. j. základne a c je dĺžka dvoch rovnakých nerovnobežných strán, potom je obvod daný vzťahom:
Obvod = a + b + 2c
kde,
- a , b sú Základy lichobežníka
- c je Rovná strana lichobežníka
Rozdiel medzi lichobežníkom a lichobežníkom
Vo všeobecnosti sú lichobežník aj lichobežník rovnaké, ale rozdiel spočíva v ich krajine pôvodu.
- Trapezium je britského pôvodu, je to štvorstranný mnohouholník a dvojrozmerný obrazec, ktorý má presne jeden pár rovnobežných strán oproti sebe. V Indii sa riadime britskou angličtinou, preto sa používa slovo Trapezium.
- Lichobežník je amerického pôvodu, je to tiež štvorstranný mnohouholník s jedným párom rovnobežných strán oproti sebe. Rovnobežné strany sú základne a ďalšie dve nerovnobežné strany sa nazývajú nohy lichobežníka.
Trapézové uhly
Lichobežník je štvoruholník a súčet všetkých uhlov štvoruholníka je 360 stupňov. Takže súčet všetkých vnútorných uhlov lichobežníka je 360 stupňov.
Pre každý pravidelný lichobežník, t. j. lichobežník, ktorého nerovnobežné strany sa rovnajú susedným uhlom vytvoreným medzi rovnobežnou čiarou a nerovnobežnou čiarou, je rovnaký. Súčet týchto dvoch uhlov je teda doplnkový.
Zoberme si príklad na podporu tohto konceptu pre rovnoramenný lichobežník ABCD, ak AB je rovnobežné s CD a AD sa rovná CD, potom vieme, že ∠A = ∠B a ∠C = ∠D, potom,
∠A + ∠B + ∠C + ∠D = 360°
Tu platí, že ∠A = ∠B a ∠C = ∠D
∠A + ∠A + ∠C + ∠C = 360°
2(∠A + ∠C) = 360°
(∠A + ∠C) = 180°
Podobne (∠B + ∠D) = 180°
Uhlopriečka lichobežníka
Trapéz je špeciálny typ štvoruholníka; teda lichobežník má tiež dve uhlopriečky. Uhlopriečky lichobežníka nemajú rovnakú dĺžku, na rozdiel od niektorých iných štvoruholníkov, ako sú obdĺžniky alebo rovnobežníky. Uhlopriečky lichobežníka nemajú rovnakú dĺžku a dĺžky uhlopriečok závisia od dĺžok podstav a uhlov lichobežníka.
Príklad: Pre rovnoramenný lichobežník ABCD je základný uhol ∠A 80°, potom nájdite druhý uhol ∠C.
Vieme, že pre rovnoramenný lichobežník ABCD,
(∠A + ∠C) = 180°
Dané, ∠A = 80°
parciálny odvodený symbol latexTeraz 80° + ∠C = 180°
∠C = 180 – 80
∠C = 100 °C
Požadovaný uhol ∠C je teda 100°
Trapézové vzorce – plocha a obvod lichobežníka
Vzorce súvisiace s lichobežníkom sú zhrnuté v nasledujúcej tabuľke:
| Nehnuteľnosť | Vzorec |
|---|---|
| Oblasť | 1/2 × ( a + b ) × h |
| Oblasť (rovnomerný lichobežník) | 1/2 × [√(c2– (a-b)2) (a+b)] |
| Obvod | a + b + c + d |
| Obvod (rovnoramenný lichobežník) | a + b + 2 c |
| Medián | (a + b)/2 |
Ľudia tiež čítajú:
- Rhombus
- Trojuholník
- Čo je vzorec na nájdenie oblasti Trapezium?
Príklady lichobežníka
Príklad 1: Nájdite štvrtú stranu lichobežníka, ak ostatné tri strany majú 8 cm, 12 cm a 16 cm a obvod je 40 cm.
Riešenie:
Obvod je daný ako súčet všetkých jeho strán. Nech dĺžka o neznáma je „x“ jednotiek.
Obvod = 40
40 = 8 + 12 + 16 + x
x = 40 – (8 + 12 + 16)
= 4 cm
Dĺžka neznámej strany je teda 4 cm
Príklad 2: Lichobežník má rovnobežné strany s dĺžkou 15 cm a 11 cm a nerovnobežné strany s dĺžkou 5 cm. Vypočítajte obvod lichobežník.
Riešenie:
Je to rovnoramenný lichobežník, pretože je jasne uvedené, že nerovnobežné strany s dĺžkou 5 cm sú rovnaké.
Podľa rovnoramenného lichobežníka, ak sú dve nerovnobežné strany lichobežníka rovnako dlhé, potom je známy ako rovnoramenný lichobežník.
Vzhľadom na to,
- a = 15 cm
- b = 11 cm
- c = 5 cm
Obvod = a + b + 2c
P = 15 + 11 + 2 (5)
P = 15 + 11 + 10
P = 36 cm
Príklad 3: Nájdite obvod lichobežníka, ktorého strany sú 12 cm, 14 cm, 16 cm a 18 cm.
Riešenie:
P = súčet všetkých strán
P = 12 + 14 + 16 + 18
P = 60 cm
Obvod lichobežníka je teda 60 cm
inak java
Príklad 4: Nájdite plochu lichobežníka, v ktorej súčet rovnobežných strán je 60 cm a jeho výška je 10 cm.
Riešenie:
Vzhľadom na to,
- Súčet rovnobežných strán 60 cm
- výška, v = 10 cm
Plocha lichobežníka, A = 1/2 × Súčet rovnobežných strán × Vzdialenosť medzi rovnobežnými stranami
Nahradením daných hodnôt,
A = 1/2 x 60 x 10
A = 30 x 10
A = 300 cm2
Preto plocha lichobežníka = 300 cm2
Cvičenie úloh na trapéz v matematike
1. Nájdite plochu lichobežníka so základňami 10 cm a 15 cm a výškou 6 cm.
2. Lichobežník má plochu 54 metrov štvorcových. Ak je jedna z podstavcov dlhá 12 metrov a výška 6 metrov, nájdite dĺžku druhej podstavy.
3. Vypočítajte obvod lichobežníka so základňami 8 cm a 14 cm a nerovnobežnými stranami 5 cm a 7 cm.
4. Určte dĺžku stredného segmentu v lichobežníku, kde základne merajú 18 cm a 30 cm.
5. V rovnoramennom lichobežníku sú uhly na jednej základni každý 45 stupňov. Nájdite miery uhlov na druhej základni. Predpokladajme, že lichobežník nie je pravý lichobežník.
Zhrnutie – Trapéz v matematike
Lichobežník je štvorstranný mnohouholník alebo štvoruholník, ktorý sa vyznačuje tým, že má jeden pár rovnobežných strán nazývaných základne, zatiaľ čo ostatné dve strany, známe ako nohy, nie sú rovnobežné. Lichobežník, ktorý je bežný v každodenných predmetoch, ako sú stoly, je pozoruhodný svojimi geometrickými vlastnosťami: má výšku, čo je kolmá vzdialenosť medzi základňami, a stred, ktorý spája stredy nerovnobežných strán a je rovnobežný so základňami.
Plocha lichobežníka sa vypočíta spriemerovaním dĺžok podstav a vynásobením výškou, pričom jeho obvod je súčtom všetkých jeho strán. S rôznymi klasifikáciami, ako sú skalénové, rovnoramenné a pravé lichobežníky, z ktorých každý má jedinečné vlastnosti strany a uhla, sú lichobežníky zásadné v praktických aplikáciách aj v geometrickej teórii.
Často kladené otázky o Trapeziu v matematike
Čo je tvar lichobežníka?
Lichobežník je štvoruholník, v ktorom je pár čiar vždy rovnobežný. Pripomína tvar stola. Jeho názov je prevzatý z gréckeho slova trapeze, čo znamená stôl.
Koľko druhov lichobežníka?
Existujú dva typy lichobežníka,
- Bežný trapéz: V ktorej sú ostatné dvojice čiar rovnaké.
- Nepravidelný trapéz: V ktorom si druhý pár riadkov nie je rovný.
Koľko paralelných strán má lichobežník?
Vieme, že lichobežník je štvoruholník s jedným párom rovnobežných strán. Lichobežník má teda pár rovnobežných čiar (stran).
Môže byť lichobežník považovaný za štvoruholník?
A má štyri strany, štyri vrcholy a štyri uhly. Preto ho možno považovať za štvoruholník, súčet všetkých štyroch vnútorných uhlov lichobežníka je 360 stupňov.
Dá sa štvorec nazvať lichobežníkom?
Lichobežník je štvoruholník s iba jedným párom rovnobežných strán a ostatné dve strany sú nerovnobežné. Ale v prípade štvorca má dva páry rovnobežných strán, preto ho nemožno považovať za lichobežník.
Sú uhlopriečky lichobežníka vždy rovnaké?
Uhlopriečky lichobežníka nemusia byť rovnaké. V prípade pravidelného mnohouholníka sú uhlopriečky rovnaké, ale v prípade nepravidelného mnohouholníka to neplatí.
Aké sú vlastnosti lichobežníka?
5 vlastností lichobežníka je:
- V lichobežníku sú základne navzájom rovnobežné.
- Lichobežník má doplnkové susedné uhly.
- Len jeden pár protiľahlých strán je rovnobežný.
- Súčet všetkých vnútorných uhlov v lichobežníku je vždy 360°.
- Čiara, ktorá spája stred nerovnobežných strán, je vždy rovnobežná so základňami.
