SILNE PREPOJENÉ KOMPONENTY - TECHCODEVIEW.COM

Silne pripojené komponenty (SCC) sú základným pojmom v teórii grafov a algoritmoch. V orientovanom grafe a Silne pripojený komponent je podmnožina vrcholov, kde každý vrchol v podmnožine je dosiahnuteľný z každého druhého vrcholu v tej istej podmnožine prechodom cez smerované hrany. Nájdenie SCC grafu môže poskytnúť dôležité poznatky o štruktúre a prepojenosti grafu s aplikáciami v rôznych oblastiach ako napr analýza sociálnych sietí, prehľadávanie webu a smerovanie siete . Tento tutoriál preskúma definíciu, vlastnosti a efektívne algoritmy na identifikáciu silne prepojených komponentov v grafových dátových štruktúrach

uml diagram java

Obsah

Čo sú pevne pripojené komponenty (SCC)?
Prečo sú dôležité pevne pripojené komponenty (SCC)?
Rozdiel medzi pripojenými a pevne pripojenými komponentmi (SCC)
Prečo nemožno použiť konvenčnú metódu DFS na nájdenie silne prepojených komponentov?
Spojenie dvoch silne prepojených komponentov pomocou jednosmernej hrany
Prístup hrubou silou na nájdenie silne prepojených komponentov
Efektívny prístup k hľadaniu silne prepojených komponentov (SCC)

1. Kosarajuov algoritmus:
2. Tarjanov algoritmus:

Záver

Čo sú pevne pripojené komponenty (SCC)?

A silne pripojený komponent orientovaného grafu je maximálny podgraf, kde je každá dvojica vrcholov vzájomne dosiahnuteľná. To znamená, že pre akékoľvek dva uzly A a B v tomto podgrafe existuje cesta z A do B a cesta z B do A.

Napríklad: Nižšie uvedený graf má dva silne prepojené komponenty {1,2,3,4} a {5,6,7}, pretože existuje cesta z každého vrcholu do každého druhého vrcholu v rovnakom silne prepojenom komponente.

Silne pripojený komponent

Prečo sú dôležité pevne pripojené komponenty (SCC)?

Pochopenie SCC je kľúčové pre rôzne aplikácie, ako napríklad:

Sieťová analýza : Identifikácia zhlukov tesne prepojených uzlov.
Optimalizácia webových prehľadávačov : Určenie častí webového grafu, ktoré sú úzko prepojené.
Riešenie závislosti : V softvéri pochopenie toho, ktoré moduly sú vzájomne závislé.

Rozdiel medzi pripojenými a pevne pripojenými komponentmi ( SCC)

Konektivita v a neorientovaný graf označuje, či sú dva vrcholy od seba dosiahnuteľné alebo nie. Hovorí sa, že dva vrcholy sú spojené, ak medzi nimi existuje cesta. Medzitým Silne pripojený sa vzťahuje len na orientované grafy . Podgraf orientovaného grafu sa považuje za an Silne pripojené komponenty (SCC) vtedy a len vtedy pre každú dvojicu vrcholov A a B , existuje cesta z A do B a cesta z B do A . Pozrime sa, prečo štandardná metóda dfs na nájdenie pripojených komponentov v grafe nemožno použiť na určenie silne prepojených komponentov.

Zvážte nasledujúci graf:

Teraz začnime a dfs zavolajte z vrcholu 1 na návštevu iných vrcholov.

Prečo nemožno použiť konvenčnú metódu DFS na nájdenie silne prepojených komponentov?

Všetky vrcholy sa dajú dosiahnuť z vrcholu 1. Ale vrcholy 1 a 5,6,7 nemôžu byť v rovnakom silne prepojenom komponente, pretože neexistuje žiadna smerovaná cesta z vrcholu 5,6 alebo 7 k vrcholu 1. Graf má dva silne pripojené komponenty {1,2,3,4} a {5,6,7}. Takže konvenčnú metódu dfs nemožno použiť na nájdenie silne prepojených komponentov.

c kód pole reťazcov

Spojenie dvoch silne prepojených komponentov pomocou jednosmernej hrany

Dva rôzne spojené komponenty sa stanú jedným komponentom, ak sa medzi vrchol jedného komponentu pridá hrana k vrcholu iného komponentu. Ale to nie je prípad silne prepojených komponentov. Dva silne spojené komponenty sa nestanú jedným pevne spojeným komponentom, ak existuje len jednosmerná hrana z jedného SCC k druhému SCC.

java vizualizér

unidrawio-(2)

Prístup hrubou silou na nájdenie silne prepojených komponentov

Jednoduchá metóda bude pre každý vrchol i (ktorý nie je súčasťou žiadneho silne komponentu) nájsť vrcholy, ktoré budú súčasťou silne prepojeného komponentu obsahujúceho vrchol i. Dva vrcholy i a j budú v rovnakom silne prepojenom komponente, ak existuje nasmerovaná cesta z vrcholu i do vrcholu j a naopak.

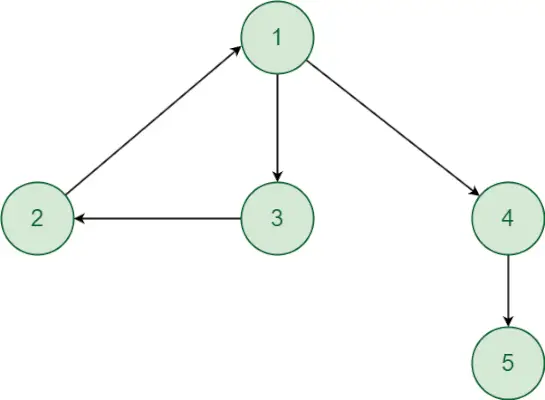
Pochopme tento prístup pomocou nasledujúceho príkladu:

Počnúc vrcholom 1. Existuje cesta z vrcholu 1 do vrcholu 2 a naopak. Podobne existuje cesta z vrcholu 1 do vrcholu 3 a naopak. Takže vrchol 2 a 3 bude v rovnakom silne prepojenom komponente ako vrchol 1. Hoci existuje smerovaná cesta z vrcholu 1 do vrcholu 4 a vrcholu 5. Ale neexistuje žiadna smerovaná cesta z vrcholu 4,5 do vrcholu 1, takže vrchol 4 a 5 nebudú v rovnakom silne prepojenom komponente ako vrchol 1. Vertex 1, 2 a 3 teda tvorí silne prepojený komponent.
Pre Vertex 2 a 3 už bol určený silne pripojený komponent.
Pre vrchol 4 existuje cesta z vrcholu 4 do vrcholu 5, ale neexistuje žiadna cesta z vrcholu 5 do vrcholu 4. Takže vrchol 4 a 5 nebudú v rovnakom silne prepojenom komponente. Vertex 4 aj Vertex 5 budú teda súčasťou Single Strongly Connected Component.
Preto budú existovať 3 silne prepojené komponenty {1,2,3}, {4} a {5}.

Nižšie je uvedená implementácia vyššie uvedeného prístupu:

C++

 #include  using namespace std; class GFG { public:  // dfs Function to reach destination  bool dfs(int curr, int des, vector>& adj, vektor & vis) { // Ak je cieľový uzol curr return true if (curr == des) { return true;  } vis[curr] = 1;  for (auto x : adj[curr]) { if (!vis[x]) { if (dfs(x, des, adj, vis)) { return true;  } } } return false;  } // Ak chcete zistiť, či existuje cesta zo zdroja do // cieľa bool isPath(int src, int des, vector>& adj) { vektor vis(adj.size() + 1, 0);  return dfs(src, des, adj, vis);  } // Funkcia na vrátenie všetkých silne prepojených // komponentov grafu.  vektor> findSCC(int n, vektor>& a) { // Uloží všetky pevne pripojené komponenty.  vektor> ans;  // Uloží, či je vrchol súčasťou akéhokoľvek silne // vektora pripojeného komponentu is_scc(n + 1, 0);  vektor> adj(n + 1);  pre (int i = 0; i< a.size(); i++) {  adj[a[i][0]].push_back(a[i][1]);  }  // Traversing all the vertices  for (int i = 1; i <= n; i++) {  if (!is_scc[i]) {  // If a vertex i is not a part of any SCC  // insert it into a new SCC list and check  // for other vertices whether they can be  // thr part of thidl ist.  vector scc;  scc.push_back(i);  for (int j = i + 1; j<= n; j++) {  // If there is a path from vertex i to  // vertex j and vice versa put vertex j  // into the current SCC list.  if (!is_scc[j] && isPath(i, j, adj)  && isPath(j, i, adj)) {  is_scc[j] = 1;  scc.push_back(j);  }  }  // Insert the SCC containing vertex i into  // the final list.  ans.push_back(scc);  }  }  return ans;  } }; // Driver Code Starts int main() {  GFG obj;  int V = 5;  vector> hrany{ { 1, 3 }, { 1, 4 }, { 2, 1 }, { 3, 2 }, { 4, 5 } };  vektor> ans = obj.findSCC(V, hrany);  cout<< 'Strongly Connected Components are:
';  for (auto x : ans) {  for (auto y : x) {  cout << y << ' ';  }  cout << '
';  } }>

Java

 import java.util.ArrayList; import java.util.List; class GFG {  // dfs Function to reach destination  boolean dfs(int curr, int des, List> adj, List vis) { // Ak je cieľový uzol curr return true if (curr == des) { return true;  } vis.set(curr, 1);  for (int x : adj.get(curr)) { if (vis.get(x) == 0) { if (dfs(x, des, adj, vis)) { return true;  } } } return false;  } // Ak chcete zistiť, či existuje cesta zo zdroja do // cieľa boolean isPath(int src, int des, List> adj) { Zoznam vis = new ArrayList(adj.size() + 1);  pre (int i = 0; i<= adj.size(); i++) {  vis.add(0);  }  return dfs(src, des, adj, vis);  }  // Function to return all the strongly connected  // component of a graph.  List> findSCC(int n, Zoznam> a) { // Uloží všetky pevne pripojené komponenty.  Zoznam> ans = new ArrayList();  // Uloží, či je vrchol súčasťou akéhokoľvek zoznamu silne // pripojených komponentov is_scc = new ArrayList (n + 1);  pre (int i = 0; i<= n; i++) {  is_scc.add(0);  }  List> adj = new ArrayList();  pre (int i = 0; i<= n; i++) {  adj.add(new ArrayList());  }  for (List hrana : a) { adj.get(edge.get(0)).add(edge.get(1));  } // Prechod cez všetky vrcholy pre (int i = 1; i<= n; i++) {  if (is_scc.get(i) == 0) {  // If a vertex i is not a part of any SCC  // insert it into a new SCC list and check  // for other vertices whether they can be  // the part of this list.  List scc = new ArrayList();  scc.add(i);  for (int j = i + 1; j<= n; j++) {  // If there is a path from vertex i to  // vertex j and vice versa, put vertex j  // into the current SCC list.  if (is_scc.get(j) == 0 && isPath(i, j, adj)  && isPath(j, i, adj)) {  is_scc.set(j, 1);  scc.add(j);  }  }  // Insert the SCC containing vertex i into  // the final list.  ans.add(scc);  }  }  return ans;  } } public class Main {  public static void main(String[] args) {  GFG obj = new GFG();  int V = 5;  List> hrany = new ArrayList();  edge.add(new ArrayList(List.of(1, 3)));  edge.add(new ArrayList(List.of(1, 4)));  edge.add(new ArrayList(List.of(2, 1)));  edge.add(new ArrayList(List.of(3, 2)));  edge.add(new ArrayList(List.of(4, 5)));  Zoznam> ans = obj.findSCC(V, hrany);  System.out.println('Silne pripojené komponenty sú:');  pre (zoznam x : ans) { for (int y : x) { System.out.print(y + ' ');  } System.out.println();  } } } // Tento kód pridal shivamgupta310570>

Python

 class GFG: # dfs Function to reach destination def dfs(self, curr, des, adj, vis): # If current node is the destination, return True if curr == des: return True vis[curr] = 1 for x in adj[curr]: if not vis[x]: if self.dfs(x, des, adj, vis): return True return False # To tell whether there is a path from source to destination def isPath(self, src, des, adj): vis = [0] * (len(adj) + 1) return self.dfs(src, des, adj, vis) # Function to return all the strongly connected components of a graph. def findSCC(self, n, a): # Stores all the strongly connected components. ans = [] # Stores whether a vertex is a part of any Strongly Connected Component is_scc = [0] * (n + 1) adj = [[] for _ in range(n + 1)] for i in range(len(a)): adj[a[i][0]].append(a[i][1]) # Traversing all the vertices for i in range(1, n + 1): if not is_scc[i]: # If a vertex i is not a part of any SCC, insert it into a new SCC list # and check for other vertices whether they can be part of this list. scc = [i] for j in range(i + 1, n + 1): # If there is a path from vertex i to vertex j and vice versa, # put vertex j into the current SCC list. if not is_scc[j] and self.isPath(i, j, adj) and self.isPath(j, i, adj): is_scc[j] = 1 scc.append(j) # Insert the SCC containing vertex i into the final list. ans.append(scc) return ans # Driver Code Starts if __name__ == '__main__': obj = GFG() V = 5 edges = [ [1, 3], [1, 4], [2, 1], [3, 2], [4, 5] ] ans = obj.findSCC(V, edges) print('Strongly Connected Components are:') for x in ans: for y in x: print(y, end=' ') print() # This code is contributed by shivamgupta310570>

 using System; using System.Collections.Generic; class GFG {  // dfs Function to reach destination  public bool Dfs(int curr, int des, List> adj, List vis) { // Ak je cieľový uzol curr, vráti hodnotu true if (curr == des) { return true;  } vis[curr] = 1;  foreach (var x in adj[curr]) { if (vis[x] == 0) { if (Dfs(x, des, adj, vis)) { return true;  } } } return false;  } // Ak chcete zistiť, či existuje cesta zo zdroja do cieľa public bool IsPath(int src, int des, List> adj) { var show = nový zoznam (prísl.počet + 1);  pre (int i = 0; i< adj.Count + 1; i++)  {  vis.Add(0);  }  return Dfs(src, des, adj, vis);  }  // Function to return all the strongly connected components of a graph  public List> FindSCC(int n, Zoznam> a) { // Uloží všetky silne prepojené komponenty var ans = new List>();  // Uloží, či je vrchol súčasťou akéhokoľvek silne pripojeného komponentu var isScc = new List (n + 1);  pre (int i = 0; i< n + 1; i++)  {  isScc.Add(0);  }  var adj = new List>(n + 1);  pre (int i = 0; i< n + 1; i++)  {  adj.Add(new List ());  } for (int i = 0; i< a.Count; i++)  {  adj[a[i][0]].Add(a[i][1]);  }  // Traversing all the vertices  for (int i = 1; i <= n; i++)  {  if (isScc[i] == 0)  {  // If a vertex i is not a part of any SCC  // insert it into a new SCC list and check  // for other vertices whether they can be  // the part of this list.  var scc = new List ();  scc.Add(i);  for (int j = i + 1; j<= n; j++)  {  // If there is a path from vertex i to  // vertex j and vice versa, put vertex j  // into the current SCC list.  if (isScc[j] == 0 && IsPath(i, j, adj) && IsPath(j, i, adj))  {  isScc[j] = 1;  scc.Add(j);  }  }  // Insert the SCC containing vertex i into  // the final list.  ans.Add(scc);  }  }  return ans;  } } // Driver Code Starts class Program {  static void Main(string[] args)  {  GFG obj = new GFG();  int V = 5;  List> hrany = nový zoznam> { nový zoznam { 1, 3 }, nový zoznam { 1, 4 }, nový zoznam { 2, 1 }, nový zoznam { 3, 2 }, nový zoznam { 4, 5} };  Zoznam> ans = obj.FindSCC(V, hrany);  Console.WriteLine('Silne pripojené komponenty sú:');  foreach (var x v ans) { foreach (var y v x) { Console.Write(y + ' ');  } Console.WriteLine();  } } } // Tento kód pridal shivamgupta310570>

Javascript

 class GFG {  // Function to reach the destination using DFS  dfs(curr, des, adj, vis) {  // If the current node is the destination, return true  if (curr === des) {  return true;  }  vis[curr] = 1;  for (let x of adj[curr]) {  if (!vis[x]) {  if (this.dfs(x, des, adj, vis)) {  return true;  }  }  }  return false;  }  // Check whether there is a path from source to destination  isPath(src, des, adj) {  const vis = new Array(adj.length + 1).fill(0);  return this.dfs(src, des, adj, vis);  }  // Function to find all strongly connected components of a graph  findSCC(n, a) {  // Stores all strongly connected components  const ans = [];  // Stores whether a vertex is part of any Strongly Connected Component  const is_scc = new Array(n + 1).fill(0);  const adj = new Array(n + 1).fill().map(() =>[]);  pre (nech i = 0; i< a.length; i++) {  adj[a[i][0]].push(a[i][1]);  }  // Traversing all the vertices  for (let i = 1; i <= n; i++) {  if (!is_scc[i]) {  // If a vertex i is not part of any SCC,  // insert it into a new SCC list and check  // for other vertices that can be part of this list.  const scc = [i];  for (let j = i + 1; j <= n; j++) {  // If there is a path from vertex i to  // vertex j and vice versa, put vertex j  // into the current SCC list.  if (!is_scc[j] && this.isPath(i, j, adj) && this.isPath(j, i, adj)) {  is_scc[j] = 1;  scc.push(j);  }  }  // Insert the SCC containing vertex i into the final list.  ans.push(scc);  }  }  return ans;  } } // Driver Code Starts const obj = new GFG(); const V = 5; const edges = [  [1, 3], [1, 4], [2, 1], [3, 2], [4, 5] ]; const ans = obj.findSCC(V, edges); console.log('Strongly Connected Components are:'); for (let x of ans) {  console.log(x.join(' ')); } // This code is contributed by shivamgupta310570>

Výkon

Strongly Connected Components are: 1 2 3 4 5>

Časová zložitosť: O(n * (n + m)), pretože pre každý pár vrcholov kontrolujeme, či medzi nimi existuje cesta.
Pomocný priestor: O(N)

program pre prvočíslo v jave

Efektívny prístup k hľadaniu silne prepojených komponentov (SCC)

Na nájdenie SCC v grafe môžeme použiť algoritmy ako napr Kosarajuov algoritmus alebo Tarjanov algoritmus . Poďme preskúmať tieto algoritmy krok za krokom.

1. Kosarajuov algoritmus :

Algoritmus Kosaraju zahŕňa dve hlavné fázy:

Vykonanie hĺbkového prvého vyhľadávania (DFS) v pôvodnom grafe :
- Najprv urobíme DFS na pôvodnom grafe a zaznamenáme konečné časy uzlov (t. j. čas, kedy DFS dokončí úplné preskúmanie uzla).
Vykonávanie DFS na transponovanom grafe :
- Potom otočíme smer všetkých hrán v grafe, aby sme vytvorili transponovaný graf.
- Ďalej vykonáme DFS na transponovanom grafe, berúc do úvahy uzly v klesajúcom poradí ich cieľových časov zaznamenaných v prvej fáze.
- Každý prechod DFS v tejto fáze nám poskytne jeden SCC.

Tu je zjednodušená verzia Kosarajuovho algoritmu:

DFS na pôvodnom grafe : Zaznamenajte časy dokončenia.
Transponujte graf : Obrátiť všetky okraje.
DFS na transponovanom grafe : Procesné uzly v poradí klesajúcich časov dokončenia na nájdenie SCC.

2. Tarjanov algoritmus :

Tarjanov algoritmus je efektívnejší, pretože nájde SCC v jedinom prechode DFS pomocou zásobníka a niektorého ďalšieho účtovníctva:

DFS Traversal : Počas DFS udržujte index pre každý uzol a najmenší index (hodnota nízkej linky), ktorý je možné dosiahnuť z uzla.
Stoh : Sledujte aktuálne uzly v zásobníku rekurzie (časť aktuálneho skúmaného SCC).
Identifikácia SCC : Keď sa hodnota nízkeho prepojenia uzla rovná jeho indexu, znamená to, že sme našli SCC. Vyberte všetky uzly zo zásobníka, kým nedosiahneme aktuálny uzol.

Tu je zjednodušený prehľad Tarjanovho algoritmu:

Inicializovaťindex>na 0.
Pre každý nenavštívený uzol vykonajte DFS.
- Nastavte index uzla a hodnotu nízkeho prepojenia.
- Zatlačte uzol na stoh.
- Pre každý susedný uzol buď vykonajte DFS, ak nie je navštívený, alebo aktualizujte hodnotu nízkeho prepojenia, ak je v zásobníku.
- Ak sa hodnota nízkeho prepojenia uzla rovná jeho indexu, vyberú uzly zo zásobníka a vytvoria SCC.

Záver

Pochopenie a nájdenie silne prepojené komponenty v orientovanom grafe je nevyhnutný pre mnohé aplikácie v informatike. Kosaraju's a Tarjanov Algoritmy sú efektívnymi spôsobmi identifikácie SCC, pričom každý má svoj vlastný prístup a výhody. Osvojením si týchto pojmov môžete lepšie analyzovať a optimalizovať štruktúru a správanie zložitých sietí.