logo

TechCodeview

Kvantilové Kvantilové grafy

Kvantilovo-kvantilový graf (q-q graf) je grafická metóda na určenie, či súbor údajov sleduje určité rozdelenie pravdepodobnosti alebo či dve vzorky údajov pochádzajú z rovnakého populácia alebo nie. Grafy Q-Q sú obzvlášť užitočné na posúdenie, či súbor údajov je normálne distribuované alebo ak nasleduje nejaké iné známe rozdelenie. Bežne sa používajú v štatistike, analýze údajov a kontrole kvality na kontrolu predpokladov a identifikáciu odchýlok od očakávaných distribúcií.

Kvantily a percentily

Kvantily sú body v súbore údajov, ktoré rozdeľujú údaje do intervalov obsahujúcich rovnaké pravdepodobnosti alebo podiely celkového rozdelenia. Často sa používajú na opis šírenia alebo distribúcie súboru údajov. Najbežnejšie kvantily sú:



  1. Medián (50. percentil) : Medián je stredná hodnota množiny údajov, keď je zoradená od najmenšej po najväčšiu. Rozdeľuje súbor údajov na dve rovnaké polovice.
  2. Kvartily (25., 50. a 75. percentil) : Kvartily rozdeľujú množinu údajov na štyri rovnaké časti. Prvý kvartil (Q1) je hodnota, pod ktorú spadá 25 % údajov, druhý kvartil (Q2) je medián a tretí kvartil (Q3) je hodnota, pod ktorú spadá 75 % údajov.
  3. Percentily : Percentily sú podobné kvartilom, ale rozdeľujú súbor údajov na 100 rovnakých častí. Napríklad 90. percentil je hodnota, pod ktorú spadá 90 % údajov.

Poznámka:

  • q-q graf je graf kvantilov prvého súboru údajov oproti kvantilom druhého súboru údajov.
  • Na referenčné účely je vynesená aj 45 % čiara; Pre ak sú vzorky z rovnakej populácie, potom sú body pozdĺž tejto čiary.


Normálna distribúcia:

Normálne rozdelenie (aka Gaussovo rozdelenie Bellova krivka) je spojité rozdelenie pravdepodobnosti reprezentujúce rozdelenie získané z náhodne generovaných reálnych hodnôt.

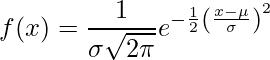
. {displaystyle f(x)={frac {1}{sigma {sqrt {2pi }}}}e^{-{frac {1}{2}}left({frac {x -mu }{sigma }} ight)^{2}}}



f(x) = Pravdepodobnosť , Rozdelenie , Funkcia mu = priemer sigma = štandard , odchýlka


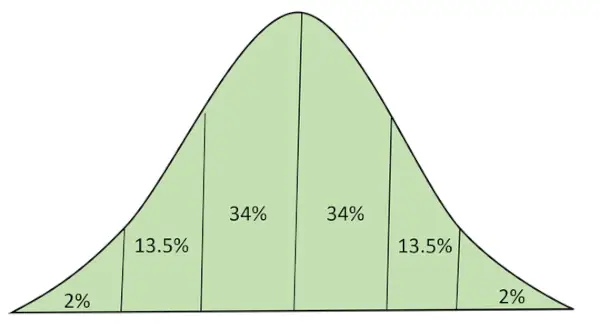
Normálna distribúcia s oblasťou pod krivkou




Ako nakresliť graf Q-Q?

Ak chcete nakresliť kvantilovo-kvantilový (Q-Q) graf, môžete postupovať podľa týchto krokov:

  1. Zbierajte údaje : Zhromaždite množinu údajov, pre ktorú chcete vytvoriť graf Q-Q. Uistite sa, že údaje sú číselné a predstavujú náhodnú vzorku zo záujmovej populácie.
  2. Zoradiť údaje : Usporiadajte údaje vo vzostupnom alebo zostupnom poradí. Tento krok je nevyhnutný pre presný výpočet kvantilov.
  3. Vyberte teoretické rozdelenie : Určite teoretické rozdelenie, s ktorým chcete porovnať svoj súbor údajov. Bežné možnosti zahŕňajú normálne rozdelenie, exponenciálne rozdelenie alebo akékoľvek iné rozloženie, ktoré dobre vyhovuje vašim údajom.
  4. Vypočítajte teoretické kvantily : Vypočítajte kvantily pre zvolené teoretické rozdelenie. Ak napríklad porovnávate s normálnym rozdelením, na nájdenie očakávaných kvantilov by ste použili funkciu inverzného kumulatívneho rozdelenia (CDF) normálneho rozdelenia.
  5. Plotovanie :
    • Vyneste zoradené hodnoty množiny údajov na os x.
    • Zodpovedajúce teoretické kvantily naneste na os y.
    • Každý údajový bod (x, y) predstavuje pár pozorovaných a očakávaných hodnôt.
    • Spojte údajové body, aby ste vizuálne skontrolovali vzťah medzi súborom údajov a teoretickým rozdelením.


Interpretácia grafu Q-Q

  • Ak body na grafe padajú približne pozdĺž priamky, znamená to, že váš súbor údajov sleduje predpokladané rozdelenie.
  • Odchýlky od priamky naznačujú odchýlky od predpokladaného rozloženia, čo si vyžaduje ďalšie skúmanie.

Skúmanie podobnosti distribúcie s grafmi Q-Q


Skúmanie podobnosti distribúcie pomocou grafov Q-Q je základnou úlohou v štatistike. Porovnanie dvoch súborov údajov s cieľom určiť, či pochádzajú z rovnakej distribúcie, je nevyhnutné na rôzne analytické účely. Ak platí predpoklad spoločného rozdelenia, zlúčenie množín údajov môže zlepšiť presnosť odhadu parametrov, ako je umiestnenie a mierka. Q-Q grafy, skratka pre kvantilovo-kvantilové grafy, ponúkajú vizuálnu metódu na hodnotenie distribučnej podobnosti. V týchto grafoch sú kvantily z jedného súboru údajov vynesené oproti kvantilom z iného. Ak sú body tesne zarovnané pozdĺž diagonálnej čiary, naznačuje to podobnosť medzi rozdeleniami. Odchýlky od tejto diagonálnej čiary naznačujú rozdiely v distribučných charakteristikách.

Zatiaľ čo testy ako napr chí-kvadrát a Kolmogorov-Smirnov testy môžu vyhodnotiť celkové rozdiely v distribúcii, grafy Q-Q poskytujú nuansovanú perspektívu priamym porovnaním kvantilov. To umožňuje analytikom rozpoznať špecifické rozdiely, ako sú posuny v umiestnení alebo zmeny v rozsahu, ktoré nemusia byť zrejmé len z formálnych štatistických testov.

Python Implementácia Q-Q Plot

Python3

import> numpy as np> import> matplotlib.pyplot as plt> import> scipy.stats as stats> # Generate example data> np.random.seed(>0>)> data>=> np.random.normal(loc>=>0>, scale>=>1>, size>=>1000>)> # Create Q-Q plot> stats.probplot(data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Normal Q-Q plot'>)> plt.xlabel(>'Theoretical quantiles'>)> plt.ylabel(>'Ordered Values'>)> plt.grid(>True>)> plt.show()> 
>
>

Výkon:



Q-Q graf


Keďže dátové body približne sledujú priamku v grafe Q-Q, naznačuje to, že súbor údajov je v súlade s predpokladaným teoretickým rozdelením, ktoré sme v tomto prípade považovali za normálne rozdelenie.

Výhody grafu Q-Q

  1. Flexibilné porovnanie : Grafy Q-Q môžu porovnávať súbory údajov rôznych veľkostí bez vyžadujúce rovnakú veľkosť vzoriek.
  2. Bezrozmerná analýza : Sú bezrozmerné, vďaka čomu sú vhodné na porovnávanie súborov údajov s rôznych jednotiek alebo mierok.
  3. Vizuálna interpretácia : Poskytuje jasnú vizuálnu reprezentáciu distribúcie údajov v porovnaní s teoretickou distribúciou.
  4. Citlivé na odchýlky : Ľahko zisťuje odchýlky od predpokladaných distribúcií a pomáha pri identifikácii nezrovnalostí v údajoch.
  5. Diagnostický nástroj : Pomáha pri hodnotení distribučných predpokladov, identifikácii odľahlých hodnôt a pochopení vzorov údajov.

Aplikácie kvantilovo-kvantilového grafu

Kvantilovo-kvantilový graf sa používa na tento účel:

  1. Posudzovanie distribučných predpokladov : Grafy Q-Q sa často používajú na vizuálnu kontrolu, či súbor údajov sleduje špecifické rozdelenie pravdepodobnosti, ako je napríklad normálne rozdelenie. Porovnaním kvantilov pozorovaných údajov s kvantilmi predpokladaného rozdelenia možno zistiť odchýlky od predpokladaného rozdelenia. Toto je kľúčové v mnohých štatistických analýzach, kde platnosť distribučných predpokladov ovplyvňuje presnosť štatistických záverov.
  2. Detekcia odľahlých hodnôt : Odľahlé hodnoty sú údajové body, ktoré sa výrazne líšia od zvyšku súboru údajov. Grafy Q-Q môžu pomôcť identifikovať odľahlé hodnoty odhalením údajových bodov, ktoré sú ďaleko od očakávaného vzoru distribúcie. Odľahlé hodnoty sa môžu objaviť ako body, ktoré sa odchyľujú od očakávanej priamky v grafe.
  3. Porovnanie distribúcií : Grafy Q-Q možno použiť na porovnanie dvoch súborov údajov, aby ste zistili, či pochádzajú z rovnakej distribúcie. To sa dosiahne vynesením kvantilov jedného súboru údajov oproti kvantilom iného súboru údajov. Ak body padajú približne pozdĺž priamky, znamená to, že tieto dva súbory údajov pochádzajú z rovnakého rozloženia.
  4. Hodnotenie normality : Grafy Q-Q sú obzvlášť užitočné na posúdenie normality súboru údajov. Ak údajové body v grafe tesne sledujú priamku, znamená to, že súbor údajov je približne normálne rozložený. Odchýlky od línie naznačujú odchýlky od normálu, čo si môže vyžadovať ďalšie skúmanie alebo neparametrické štatistické techniky.
  5. Validácia modelu : V oblastiach ako ekonometria a strojové učenie sa grafy Q-Q používajú na overenie prediktívnych modelov. Porovnaním kvantilov pozorovaných odpovedí s kvantilmi predpovedanými modelom je možné posúdiť, ako dobre model zodpovedá údajom. Odchýlky od očakávaného vzoru môžu naznačovať oblasti, v ktorých model potrebuje zlepšenie.
  6. Kontrola kvality : Q-Q grafy sa používajú v procesoch kontroly kvality na monitorovanie distribúcie nameraných alebo pozorovaných hodnôt v čase alebo v rôznych šaržiach. Odchýlky od očakávaných vzorov v grafe môžu signalizovať zmeny v základných procesoch, čo si vyžiada ďalšie skúmanie.

Typy Q-Q grafov

Existuje niekoľko typov grafov Q-Q bežne používaných v štatistike a analýze údajov, pričom každý je vhodný pre rôzne scenáre alebo účely:

  1. Normálna distribúcia : Symetrické rozdelenie, kde graf Q-Q zobrazuje body približne pozdĺž diagonálnej čiary, ak sa údaje pridržiavajú normálneho rozdelenia.
  2. Pravoskosená distribúcia : Distribúcia, kde graf Q-Q zobrazuje vzor, ​​v ktorom sa pozorované kvantily odchyľujú od priamky smerom k hornému koncu, čo naznačuje dlhší koniec na pravej strane.
  3. Distribúcia skosená doľava : Distribúcia, kde by graf Q-Q vykazoval vzor, ​​v ktorom sa pozorované kvantily odchyľujú od priamky smerom k dolnému koncu, čo naznačuje dlhší koniec na ľavej strane.
  4. Nedostatočne rozptýlená distribúcia : Distribúcia, kde by graf Q-Q ukázal pozorované kvantily zhlukované tesnejšie okolo diagonálnej čiary v porovnaní s teoretickými kvantilmi, čo naznačuje nižší rozptyl.
  5. Príliš rozptýlená distribúcia : Distribúcia, kde graf Q-Q zobrazuje pozorované kvantily viac rozložené alebo odchyľujúce sa od diagonálnej čiary, čo naznačuje vyšší rozptyl alebo rozptyl v porovnaní s teoretickým rozložením.

Python3

import> numpy as np> import> matplotlib.pyplot as plt> import> scipy.stats as stats> # Generate a random sample from a normal distribution> normal_data>=> np.random.normal(loc>=>0>, scale>=>1>, size>=>1000>)> # Generate a random sample from a right-skewed distribution (exponential distribution)> right_skewed_data>=> np.random.exponential(scale>=>1>, size>=>1000>)> # Generate a random sample from a left-skewed distribution (negative exponential distribution)> left_skewed_data>=> ->np.random.exponential(scale>=>1>, size>=>1000>)> # Generate a random sample from an under-dispersed distribution (truncated normal distribution)> under_dispersed_data>=> np.random.normal(loc>=>0>, scale>=>0.5>, size>=>1000>)> under_dispersed_data>=> under_dispersed_data[(under_dispersed_data>>->1>) & (under_dispersed_data <>1>)]># Truncate> # Generate a random sample from an over-dispersed distribution (mixture of normals)> over_dispersed_data>=> np.concatenate((np.random.normal(loc>=>->2>, scale>=>1>, size>=>500>),> >np.random.normal(loc>=>2>, scale>=>1>, size>=>500>)))> # Create Q-Q plots> plt.figure(figsize>=>(>15>,>10>))> plt.subplot(>2>,>3>,>1>)> stats.probplot(normal_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Normal Distribution'>)> plt.subplot(>2>,>3>,>2>)> stats.probplot(right_skewed_data, dist>=>'expon'>, plot>=>plt)> plt.title(>'Q-Q Plot - Right-skewed Distribution'>)> plt.subplot(>2>,>3>,>3>)> stats.probplot(left_skewed_data, dist>=>'expon'>, plot>=>plt)> plt.title(>'Q-Q Plot - Left-skewed Distribution'>)> plt.subplot(>2>,>3>,>4>)> stats.probplot(under_dispersed_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Under-dispersed Distribution'>)> plt.subplot(>2>,>3>,>5>)> stats.probplot(over_dispersed_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Over-dispersed Distribution'>)> plt.tight_layout()> plt.show()> 
>
>

Výkon:


Q-Q graf pre rôzne distribúcie

lyžička vs polievková lyžica