AVL strom:
AVL strom je samovyvažujúci binárny vyhľadávací strom ( BST ), kde rozdiel medzi výškami ľavého a pravého podstromu nemôže byť väčší ako jeden pre všetky uzly.
Príklad stromu AVL:
Vyššie uvedený strom je AVL, pretože rozdiely medzi výškami ľavého a pravého podstromu pre každý uzol sú menšie alebo rovné 1.
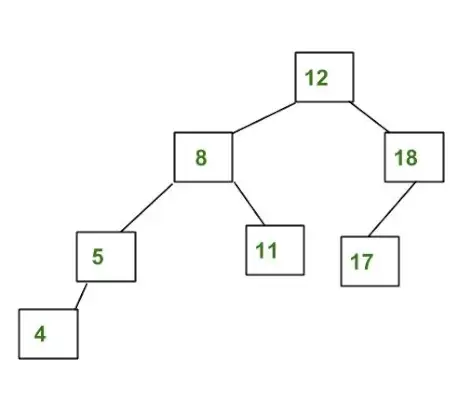
Príklad stromu, ktorý NIE JE stromom AVL:

Vyššie uvedený strom nie je AVL, pretože rozdiely medzi výškami ľavého a pravého podstromu pre 8 a 12 sú väčšie ako 1.
Prečo AVL Trees?
Väčšina operácií BST (napr. vyhľadávanie, max, min, vloženie, vymazanie atď.) trvá O(h) čas kde h je výška BST. Náklady na tieto operácie sa môžu zvýšiť O(n) pre skosený binárny strom . Ak dbáme na to, aby výška stromu zostala O(log(n)) po každom vložení a vymazaní, potom môžeme zaručiť hornú hranicu O(log(n)) pre všetky tieto operácie. Výška stromu AVL je vždy O(log(n)) kde n je počet uzlov v strome.
Vkladanie v strome AVL:
Aby sme sa uistili, že daný strom zostane AVL po každom vložení, musíme rozšíriť štandardnú operáciu vloženia BST, aby sme vykonali určité opätovné vyváženie.
Nasledujú dve základné operácie, ktoré možno vykonať na vyváženie BST bez porušenia vlastnosti BST (klávesy (vľavo)
- Ľavá rotácia
- Pravá rotácia
T1, T2 and T3 are subtrees of the tree, rooted with y (on the left side) or x (on the right side) y x / Right Rotation / x T3 - - - - - - ->T1 a / <- - - - - - - / T1 T2 Left Rotation T2 T3 Keys in both of the above trees follow the following order keys(T1) < key(x) < keys(T2) < key(y) < keys(T3) So BST property is not violated anywhere.>Odporúčaný postup Vkladanie stromu AVL Vyskúšajte to!
Postup pri vkladaní:
Nech je novo vložený uzol In
- Vykonajte štandard BST vložiť pre In .
- Začať z In , cestujte hore a nájdite prvého nevyvážený uzol . Nechaj S byť prvým nevyváženým uzlom, a byť dieťa z S ktorý prichádza na cestu z In do S a X byť vnúča z S ktorý prichádza na cestu z In do S .
- Znovu vyvážte strom vykonaním vhodných rotácií na podstrome, ktorý má korene s s. Môžu existovať 4 možné prípady, ktoré je potrebné riešiť ako x, y a S možno usporiadať 4 spôsobmi.
- Nasledujú 4 možné usporiadania:
- y je ľavé dieťa z a x je ľavé dieťa y (ľavé ľavé veľké písmená)
- y je ľavé dieťa z a x je pravé dieťa y (ľavý a pravý prípad)
- y je správnym potomkom z a x je správnym potomkom y (správne veľké písmená)
- y je pravé dieťa z a x je ľavé dieťa y (pravé ľavé veľké písmená)
Nasledujú operácie, ktoré sa majú vykonať vo vyššie uvedených 4 prípadoch. Vo všetkých prípadoch musíme iba my znovu vyvážiť podstrom zakorenený s S a celý strom sa vyrovná podľa výšky podstromu (po príslušnom otočení) zakoreneného S bude rovnaký ako pred vložením.
1. Ľavé ľavé puzdro
T1, T2, T3 and T4 are subtrees. z y / / y T4 Right Rotate (z) x z / - - - - - - - - ->/ / x T3 T1 T2 T3 T4 / T1 T2>
2. Ľavé Pravé puzdro
z z x / / / y T4 Left Rotate (y) x T4 Right Rotate(z) y z / - - - - - - - - ->/ - - - - - - - -> / / T1 x y T3 T1 T2 T3 T4 / / T2 T3 T1 T2>
3. Pravý Pravý prípad
z y / / T1 y Left Rotate(z) z x / - - - - - - - ->/ / T2 x T1 T2 T3 T4 / T3 T4>
4. Pravé ľavé puzdro
z z x / / / T1 y Right Rotate (y) T1 x Left Rotate(z) z y / - - - - - - - - ->/ - - - - - - - -> / / x T4 T2 y T1 T2 T3 T4 / / T2 T3 T3 T4>
Ilustrácia vloženia do stromu AVL





Prístup:
Myšlienkou je použiť rekurzívny BST insert, po vložení dostaneme ukazovatele na všetkých predkov jeden po druhom spôsobom zdola nahor. Na cestu nahor teda nepotrebujeme rodičovský ukazovateľ. Samotný rekurzívny kód putuje nahor a navštívi všetkých predkov novo vloženého uzla.
Pri implementácii myšlienky postupujte podľa krokov uvedených nižšie:
- Vykonajte normálne Vloženie BST.
- Aktuálny uzol musí byť jedným z predkov novo vloženého uzla. Aktualizujte výška aktuálneho uzla.
- Získajte faktor rovnováhy (ľavá výška podstromu – pravá výška podstromu) aktuálneho uzla.
- Ak je koeficient rovnováhy väčší ako 1, potom je aktuálny uzol nevyvážený a my sme buď v Ľavé ľavé puzdro alebo vľavo Pravé puzdro . Ak chcete skontrolovať, či áno ľavé ľavé puzdro alebo nie, porovnajte novo vložený kľúč s kľúčom v ľavý koreň podstromu .
- Ak je bilančný faktor menší ako -1 , potom je aktuálny uzol nevyvážený a nachádzame sa buď v prípade Right Right alebo Right-Left. Ak chcete skontrolovať, či ide o prípad Right Right alebo nie, porovnajte novo vložený kľúč s kľúčom v pravom koreni podstromu.
Nižšie je uvedená implementácia vyššie uvedeného prístupu:
C++14
// C++ program to insert a node in AVL tree> #include> using> namespace> std;> > // An AVL tree node> class> Node> {> >public>:> >int> key;> >Node *left;> >Node *right;> >int> height;> };> > // A utility function to get the> // height of the tree> int> height(Node *N)> {> >if> (N == NULL)> >return> 0;> >return> N->výška;> }> > // A utility function to get maximum> // of two integers> int> max(>int> a,>int> b)> {> >return> (a>b)? a: b;> }> > /* Helper function that allocates a> >new node with the given key and> >NULL left and right pointers. */> Node* newNode(>int> key)> {> >Node* node =>new> Node();> >node->kľúč = kľúč;> >node->vľavo = NULL;> >node->vpravo = NULL;> >node->výška = 1;>// new node is initially> >// added at leaf> >return>(node);> }> > // A utility function to right> // rotate subtree rooted with y> // See the diagram given above.> Node *rightRotate(Node *y)> {> >Node *x = y->vľavo;> >Node *T2 = x->správny;> > >// Perform rotation> >x->vpravo = y;> >y->vľavo = T2;> > >// Update heights> >y->výška = max(výška(y->vľavo),> >height(y->vpravo)) + 1;> >x->výška = max(výška(x->vľavo),> >height(x->vpravo)) + 1;> > >// Return new root> >return> x;> }> > // A utility function to left> // rotate subtree rooted with x> // See the diagram given above.> Node *leftRotate(Node *x)> {> >Node *y = x->správny;> >Node *T2 = y->vľavo;> > >// Perform rotation> >y->vľavo = x;> >x->vpravo = T2;> > >// Update heights> >x->výška = max(výška(x->vľavo),> >height(x->vpravo)) + 1;> >y->výška = max(výška(y->vľavo),> >height(y->vpravo)) + 1;> > >// Return new root> >return> y;> }> > // Get Balance factor of node N> int> getBalance(Node *N)> {> >if> (N == NULL)> >return> 0;> >return> height(N->vľavo) - výška(N->vpravo);> }> > // Recursive function to insert a key> // in the subtree rooted with node and> // returns the new root of the subtree.> Node* insert(Node* node,>int> key)> {> >/* 1. Perform the normal BST insertion */> >if> (node == NULL)> >return>(newNode(key));> > >if> (key key)> >node->left = insert(uzol->left, key);> >else> if> (key>uzol->kľúč)> >node->vpravo = vložiť(uzol->vpravo, kľúč);> >else> // Equal keys are not allowed in BST> >return> node;> > >/* 2. Update height of this ancestor node */> >node->výška = 1 + max(výška(uzol->vľavo),> >height(node->správny));> > >/* 3. Get the balance factor of this ancestor> >node to check whether this node became> >unbalanced */> >int> balance = getBalance(node);> > >// If this node becomes unbalanced, then> >// there are 4 cases> > >// Left Left Case> >if> (balance>1 kláves && vľavo->kláves)> >return> rightRotate(node);> > >// Right Right Case> >if> (balance node->vpravo->kláves)> >return> leftRotate(node);> > >// Left Right Case> >if> (balance>1 kláves &&> uzol->ľavý->kláves)> >{> >node->doľava = doľavaOtočiť(uzol->doľava);> >return> rightRotate(node);> >}> > >// Right Left Case> >if> (balance <-1 && key right->kľúč)> >{> >node->vpravo = vpravoRotate(uzol->vpravo);> >return> leftRotate(node);> >}> > >/* return the (unchanged) node pointer */> >return> node;> }> > // A utility function to print preorder> // traversal of the tree.> // The function also prints height> // of every node> void> preOrder(Node *root)> {> >if>(root != NULL)> >{> >cout ' '; preOrder(root->vľavo); preOrder(root->right); } } // Kód ovládača int main() { Node *root = NULL; /* Zostrojenie stromu uvedené na obrázku vyššie */ root = insert(root, 10); root = insert(root, 20); root = insert(root, 30); root = insert(root, 40); root = insert(root, 50); root = insert(root, 25); /* Skonštruovaný strom AVL by bol 30 / 20 40 / 10 25 50 */ cout<< 'Preorder traversal of the ' 'constructed AVL tree is
'; preOrder(root); return 0; } // This code is contributed by // rathbhupendra> |
>
>
C
// C program to insert a node in AVL tree> #include> #include> > // An AVL tree node> struct> Node> {> >int> key;> >struct> Node *left;> >struct> Node *right;> >int> height;> };> > // A utility function to get the height of the tree> int> height(>struct> Node *N)> {> >if> (N == NULL)> >return> 0;> >return> N->výška;> }> > // A utility function to get maximum of two integers> int> max(>int> a,>int> b)> {> >return> (a>b)? a: b;> }> > /* Helper function that allocates a new node with the given key and> >NULL left and right pointers. */> struct> Node* newNode(>int> key)> {> >struct> Node* node = (>struct> Node*)> >malloc>(>sizeof>(>struct> Node));> >node->kľúč = kľúč;> >node->vľavo = NULL;> >node->vpravo = NULL;> >node->výška = 1;>// new node is initially added at leaf> >return>(node);> }> > // A utility function to right rotate subtree rooted with y> // See the diagram given above.> struct> Node *rightRotate(>struct> Node *y)> {> >struct> Node *x = y->vľavo;> >struct> Node *T2 = x->správny;> > >// Perform rotation> >x->vpravo = y;> >y->vľavo = T2;> > >// Update heights> >y->výška = max(výška(y->vľavo),> >height(y->vpravo)) + 1;> >x->výška = max(výška(x->vľavo),> >height(x->vpravo)) + 1;> > >// Return new root> >return> x;> }> > // A utility function to left rotate subtree rooted with x> // See the diagram given above.> struct> Node *leftRotate(>struct> Node *x)> {> >struct> Node *y = x->správny;> >struct> Node *T2 = y->vľavo;> > >// Perform rotation> >y->vľavo = x;> >x->vpravo = T2;> > >// Update heights> >x->výška = max(výška(x->vľavo),> >height(x->vpravo)) + 1;> >y->výška = max(výška(y->vľavo),> >height(y->vpravo)) + 1;> > >// Return new root> >return> y;> }> > // Get Balance factor of node N> int> getBalance(>struct> Node *N)> {> >if> (N == NULL)> >return> 0;> >return> height(N->vľavo) - výška(N->vpravo);> }> > // Recursive function to insert a key in the subtree rooted> // with node and returns the new root of the subtree.> struct> Node* insert(>struct> Node* node,>int> key)> {> >/* 1. Perform the normal BST insertion */> >if> (node == NULL)> >return>(newNode(key));> > >if> (key key)> >node->left = insert(uzol->left, key);> >else> if> (key>uzol->kľúč)> >node->vpravo = vložiť(uzol->vpravo, kľúč);> >else> // Equal keys are not allowed in BST> >return> node;> > >/* 2. Update height of this ancestor node */> >node->výška = 1 + max(výška(uzol->vľavo),> >height(node->správny));> > >/* 3. Get the balance factor of this ancestor> >node to check whether this node became> >unbalanced */> >int> balance = getBalance(node);> > >// If this node becomes unbalanced, then> >// there are 4 cases> > >// Left Left Case> >if> (balance>1 kláves && vľavo->kláves)> >return> rightRotate(node);> > >// Right Right Case> >if> (balance node->vpravo->kláves)> >return> leftRotate(node);> > >// Left Right Case> >if> (balance>1 kláves &&> uzol->ľavý->kláves)> >{> >node->doľava = doľavaOtočiť(uzol->doľava);> >return> rightRotate(node);> >}> > >// Right Left Case> >if> (balance <-1 && key right->kľúč)> >{> >node->vpravo = vpravoRotate(uzol->vpravo);> >return> leftRotate(node);> >}> > >/* return the (unchanged) node pointer */> >return> node;> }> > // A utility function to print preorder traversal> // of the tree.> // The function also prints height of every node> void> preOrder(>struct> Node *root)> {> >if>(root != NULL)> >{> >printf>(>'%d '>, root->kľúč);> >preOrder(root->vľavo);> >preOrder(root->správny);> >}> }> > /* Driver program to test above function*/> int> main()> {> >struct> Node *root = NULL;> > >/* Constructing tree given in the above figure */> >root = insert(root, 10);> >root = insert(root, 20);> >root = insert(root, 30);> >root = insert(root, 40);> >root = insert(root, 50);> >root = insert(root, 25);> > >/* The constructed AVL Tree would be> >30> >/> >20 40> >/> >10 25 50> >*/> > >printf>(>'Preorder traversal of the constructed AVL'> >' tree is
'>);> >preOrder(root);> > >return> 0;> }> |
>
>
Java
// Java program for insertion in AVL Tree> class> Node {> >int> key, height;> >Node left, right;> > >Node(>int> d) {> >key = d;> >height =>1>;> >}> }> > class> AVLTree {> > >Node root;> > >// A utility function to get the height of the tree> >int> height(Node N) {> >if> (N ==>null>)> >return> 0>;> > >return> N.height;> >}> > >// A utility function to get maximum of two integers> >int> max(>int> a,>int> b) {> >return> (a>b) ? a: b;> >}> > >// A utility function to right rotate subtree rooted with y> >// See the diagram given above.> >Node rightRotate(Node y) {> >Node x = y.left;> >Node T2 = x.right;> > >// Perform rotation> >x.right = y;> >y.left = T2;> > >// Update heights> >y.height = max(height(y.left), height(y.right)) +>1>;> >x.height = max(height(x.left), height(x.right)) +>1>;> > >// Return new root> >return> x;> >}> > >// A utility function to left rotate subtree rooted with x> >// See the diagram given above.> >Node leftRotate(Node x) {> >Node y = x.right;> >Node T2 = y.left;> > >// Perform rotation> >y.left = x;> >x.right = T2;> > >// Update heights> >x.height = max(height(x.left), height(x.right)) +>1>;> >y.height = max(height(y.left), height(y.right)) +>1>;> > >// Return new root> >return> y;> >}> > >// Get Balance factor of node N> >int> getBalance(Node N) {> >if> (N ==>null>)> >return> 0>;> > >return> height(N.left) - height(N.right);> >}> > >Node insert(Node node,>int> key) {> > >/* 1. Perform the normal BST insertion */> >if> (node ==>null>)> >return> (>new> Node(key));> > >if> (key node.left = insert(node.left, key); else if (key>node.key) node.right = insert(uzol.right, key); else // Nie sú povolené duplicitné kľúče návratový uzol; /* 2. Aktualizácia výšky tohto uzla predka */ node.height = 1 + max(height(uzol.left), height(node.right)); /* 3. Získajte koeficient rovnováhy tohto predchodcu, aby ste skontrolovali, či sa tento uzol stal nevyváženým */ int balance = getBalance(node); // Ak sa tento uzol stane nevyváženým, potom // existujú 4 prípady Left Left Case if (zostatok> 1 && key return rightRotate(node); // Right Right Case if (zostatok<-1 && key>node.right.key) return leftRotate(uzol); // Left Right Case if (zostatok> 1 && kľúč> node.left.key) { node.left = leftRotate(node.left); return rightRotate(uzol); } // Pravé ľavé veľké a malé písmená if (zostatok<-1 && key node.right = rightRotate(node.right); return leftRotate(node); } /* return the (unchanged) node pointer */ return node; } // A utility function to print preorder traversal // of the tree. // The function also prints height of every node void preOrder(Node node) { if (node != null) { System.out.print(node.key + ' '); preOrder(node.left); preOrder(node.right); } } public static void main(String[] args) { AVLTree tree = new AVLTree(); /* Constructing tree given in the above figure */ tree.root = tree.insert(tree.root, 10); tree.root = tree.insert(tree.root, 20); tree.root = tree.insert(tree.root, 30); tree.root = tree.insert(tree.root, 40); tree.root = tree.insert(tree.root, 50); tree.root = tree.insert(tree.root, 25); /* The constructed AVL Tree would be 30 / 20 40 / 10 25 50 */ System.out.println('Preorder traversal' + ' of constructed tree is : '); tree.preOrder(tree.root); } } // This code has been contributed by Mayank Jaiswal> |
>
>
Python3
# Python code to insert a node in AVL tree> > # Generic tree node class> class> TreeNode(>object>):> >def> __init__(>self>, val):> >self>.val>=> val> >self>.left>=> None> >self>.right>=> None> >self>.height>=> 1> > # AVL tree class which supports the> # Insert operation> class> AVL_Tree(>object>):> > ># Recursive function to insert key in> ># subtree rooted with node and returns> ># new root of subtree.> >def> insert(>self>, root, key):> > ># Step 1 - Perform normal BST> >if> not> root:> >return> TreeNode(key)> >elif> key root.left = self.insert(root.left, key) else: root.right = self.insert(root.right, key) # Step 2 - Update the height of the # ancestor node root.height = 1 + max(self.getHeight(root.left), self.getHeight(root.right)) # Step 3 - Get the balance factor balance = self.getBalance(root) # Step 4 - If the node is unbalanced, # then try out the 4 cases # Case 1 - Left Left if balance>1 a kľúč sa vráti self.rightRotate(root) # Prípad 2 - Right Right, ak je rovnováha<-1 and key>root.right.val: return self.leftRotate(root) # Prípad 3 - Left Right if balance> 1 and key> root.left.val: root.left = self.leftRotate(root.left) return self.rightRotate(root ) # Prípad 4 - Pravý Ľavý pri rovnováhe<-1 and key root.right = self.rightRotate(root.right) return self.leftRotate(root) return root def leftRotate(self, z): y = z.right T2 = y.left # Perform rotation y.left = z z.right = T2 # Update heights z.height = 1 + max(self.getHeight(z.left), self.getHeight(z.right)) y.height = 1 + max(self.getHeight(y.left), self.getHeight(y.right)) # Return the new root return y def rightRotate(self, z): y = z.left T3 = y.right # Perform rotation y.right = z z.left = T3 # Update heights z.height = 1 + max(self.getHeight(z.left), self.getHeight(z.right)) y.height = 1 + max(self.getHeight(y.left), self.getHeight(y.right)) # Return the new root return y def getHeight(self, root): if not root: return 0 return root.height def getBalance(self, root): if not root: return 0 return self.getHeight(root.left) - self.getHeight(root.right) def preOrder(self, root): if not root: return print('{0} '.format(root.val), end='') self.preOrder(root.left) self.preOrder(root.right) # Driver program to test above function myTree = AVL_Tree() root = None root = myTree.insert(root, 10) root = myTree.insert(root, 20) root = myTree.insert(root, 30) root = myTree.insert(root, 40) root = myTree.insert(root, 50) root = myTree.insert(root, 25) '''The constructed AVL Tree would be 30 / 20 40 / 10 25 50''' # Preorder Traversal print('Preorder traversal of the', 'constructed AVL tree is') myTree.preOrder(root) print() # This code is contributed by Ajitesh Pathak> |
>
>
C#
// C# program for insertion in AVL Tree> using> System;> > class> Node> {> >public> int> key, height;> >public> Node left, right;> > >public> Node(>int> d)> >{> >key = d;> >height = 1;> >}> }> > public> class> AVLTree> {> > >Node root;> > >// A utility function to get> >// the height of the tree> >int> height(Node N)> >{> >if> (N ==>null>)> >return> 0;> > >return> N.height;> >}> > >// A utility function to get> >// maximum of two integers> >int> max(>int> a,>int> b)> >{> >return> (a>b) ? a: b;> >}> > >// A utility function to right> >// rotate subtree rooted with y> >// See the diagram given above.> >Node rightRotate(Node y)> >{> >Node x = y.left;> >Node T2 = x.right;> > >// Perform rotation> >x.right = y;> >y.left = T2;> > >// Update heights> >y.height = max(height(y.left),> >height(y.right)) + 1;> >x.height = max(height(x.left),> >height(x.right)) + 1;> > >// Return new root> >return> x;> >}> > >// A utility function to left> >// rotate subtree rooted with x> >// See the diagram given above.> >Node leftRotate(Node x)> >{> >Node y = x.right;> >Node T2 = y.left;> > >// Perform rotation> >y.left = x;> >x.right = T2;> > >// Update heights> >x.height = max(height(x.left),> >height(x.right)) + 1;> >y.height = max(height(y.left),> >height(y.right)) + 1;> > >// Return new root> >return> y;> >}> > >// Get Balance factor of node N> >int> getBalance(Node N)> >{> >if> (N ==>null>)> >return> 0;> > >return> height(N.left) - height(N.right);> >}> > >Node insert(Node node,>int> key)> >{> > >/* 1. Perform the normal BST insertion */> >if> (node ==>null>)> >return> (>new> Node(key));> > >if> (key node.left = insert(node.left, key); else if (key>node.key) node.right = insert(uzol.right, key); else // Nie sú povolené duplicitné kľúče návratový uzol; /* 2. Aktualizácia výšky tohto uzla predka */ node.height = 1 + max(height(uzol.left), height(node.right)); /* 3. Získajte koeficient rovnováhy tohto predchodcu, aby ste skontrolovali, či sa tento uzol stal nevyváženým */ int balance = getBalance(node); // Ak sa tento uzol stane nevyváženým, potom // existujú 4 prípady Left Left Case if (zostatok> 1 && key return rightRotate(node); // Right Right Case if (balance node.right.key) return leftRotate(node) ; // Left Right Case if (balance> 1 && key> node.left.key) { node.left = leftRotate(uzol.left return rightRotate(uzol) } // Right Left Case if (balance<-1 && key < node.right.key) { node.right = rightRotate(node.right); return leftRotate(node); } /* return the (unchanged) node pointer */ return node; } // A utility function to print preorder traversal // of the tree. // The function also prints height of every node void preOrder(Node node) { if (node != null) { Console.Write(node.key + ' '); preOrder(node.left); preOrder(node.right); } } // Driver code public static void Main(String[] args) { AVLTree tree = new AVLTree(); /* Constructing tree given in the above figure */ tree.root = tree.insert(tree.root, 10); tree.root = tree.insert(tree.root, 20); tree.root = tree.insert(tree.root, 30); tree.root = tree.insert(tree.root, 40); tree.root = tree.insert(tree.root, 50); tree.root = tree.insert(tree.root, 25); /* The constructed AVL Tree would be 30 / 20 40 / 10 25 50 */ Console.Write('Preorder traversal' + ' of constructed tree is : '); tree.preOrder(tree.root); } } // This code has been contributed // by PrinciRaj1992> |
>
>
Javascript
> > >// JavaScript program for insertion in AVL Tree> >class Node {> >constructor(d) {> >this>.key = d;> >this>.height = 1;> >this>.left =>null>;> >this>.right =>null>;> >}> >}> > >class AVLTree {> >constructor() {> >this>.root =>null>;> >}> > >// A utility function to get> >// the height of the tree> >height(N) {> >if> (N ==>null>)>return> 0;> > >return> N.height;> >}> > >// A utility function to get> >// maximum of two integers> >max(a, b) {> >return> a>b ? a: b;> >}> > >// A utility function to right> >// rotate subtree rooted with y> >// See the diagram given above.> >rightRotate(y) {> >var> x = y.left;> >var> T2 = x.right;> > >// Perform rotation> >x.right = y;> >y.left = T2;> > >// Update heights> >y.height =>this>.max(>this>.height(y.left),> >this>.height(y.right)) + 1;> >x.height =>this>.max(>this>.height(x.left),> >this>.height(x.right)) + 1;> > >// Return new root> >return> x;> >}> > >// A utility function to left> >// rotate subtree rooted with x> >// See the diagram given above.> >leftRotate(x) {> >var> y = x.right;> >var> T2 = y.left;> > >// Perform rotation> >y.left = x;> >x.right = T2;> > >// Update heights> >x.height =>this>.max(>this>.height(x.left),> >this>.height(x.right)) + 1;> >y.height =>this>.max(>this>.height(y.left),> >this>.height(y.right)) + 1;> > >// Return new root> >return> y;> >}> > >// Get Balance factor of node N> >getBalance(N) {> >if> (N ==>null>)>return> 0;> > >return> this>.height(N.left) ->this>.height(N.right);> >}> > >insert(node, key) {> >/* 1. Perform the normal BST insertion */> >if> (node ==>null>)>return> new> Node(key);> > >if> (key node.left = this.insert(node.left, key); else if (key>node.key) node.right = this.insert(uzol.right, key); // Duplicitné kľúče nie sú povolené else return node; /* 2. Aktualizácia výšky tohto uzla predka */ node.height = 1 + this.max(this.height(uzol.left), this.height(node.right)); /* 3. Získajte koeficient rovnováhy tohto predchodcu, aby ste skontrolovali, či sa tento uzol stal nevyváženým */ var balance = this.getBalance(node); // Ak sa tento uzol stane nevyváženým, potom // existujú 4 prípady Left Left Case if (zostatok> 1 kláves && return this.rightRotate(node); // Right Right Case if (balance node.right.key) vráti toto. leftRotate(node) // Left Right Case if (balance> 1 && key> node.left.key) { node.left = this.leftRotate(uzol.left) return this.rightRotate(node); Left Case if (zostatok<-1 && key < node.right.key) { node.right = this.rightRotate(node.right); return this.leftRotate(node); } /* return the (unchanged) node pointer */ return node; } // A utility function to print preorder traversal // of the tree. // The function also prints height of every node preOrder(node) { if (node != null) { document.write(node.key + ' '); this.preOrder(node.left); this.preOrder(node.right); } } } // Driver code var tree = new AVLTree(); /* Constructing tree given in the above figure */ tree.root = tree.insert(tree.root, 10); tree.root = tree.insert(tree.root, 20); tree.root = tree.insert(tree.root, 30); tree.root = tree.insert(tree.root, 40); tree.root = tree.insert(tree.root, 50); tree.root = tree.insert(tree.root, 25); /* The constructed AVL Tree would be 30 / 20 40 / 10 25 50 */ document.write( 'Preorder traversal of the ' + 'constructed AVL tree is ' ); tree.preOrder(tree.root);> |
>
>Výkon
Preorder traversal of the constructed AVL tree is 30 20 10 25 40 50>
Analýza zložitosti
Časová zložitosť: O(log(n)), na vloženie
Pomocný priestor: O(1)
ukážkový javascript
Operácie otáčania (otočenie doľava a doprava) trvajú konštantne, pretože sa tam mení len niekoľko ukazovateľov. Aktualizácia výšky a získanie súčiniteľa vyváženia tiež trvá konštantne. Časová zložitosť vložky AVL teda zostáva rovnaká ako vložka BST, čo je O(h), kde h je výška stromu. Keďže strom AVL je vyvážený, výška je O(Logn). Časová zložitosť vložky AVL je teda O(Logn).
Porovnanie s Red Black Tree:
Strom AVL a ďalšie samovyvažovacie vyhľadávacie stromy, ako napríklad Red Black, sú užitočné na vykonanie všetkých základných operácií v čase O(log n). AVL stromy sú vyváženejšie v porovnaní s červeno-čiernymi stromami, ale môžu spôsobiť viac rotácií počas vkladania a odstraňovania. Takže ak vaša aplikácia zahŕňa veľa častých vkladov a vymazávaní, mali by ste uprednostniť stromy Red Black. A ak sú vkladanie a vymazávanie menej časté a vyhľadávanie je častejšia operácia, potom by mal byť strom AVL uprednostnený pred stromom Red Black Tree .
Nasleduje príspevok na odstránenie v strome AVL:
AVL strom | Sada 2 (odstránenie)
