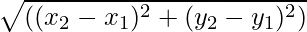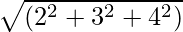VEĽKOSŤ VEKTORA – DEFINÍCIA, VZOREC, PRÍKLADY A ČASTO KLADENÉ OTÁZKY

Vektorové veličiny sú veličiny, ktoré majú smer aj veľkosť. Veľkosť vektora je dĺžka vektora. Je daná číselnou hodnotou vektora a keďže predstavuje dĺžku vektora, je vždy kladná. Pre akýkoľvek vektor 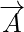overrightarrow{A} jeho veľkosť je reprezentovaná ako .

V tomto článku sa dozvieme viac o veľkosti vektora, jeho vzorci, príkladoch a ďalších.

Obsah

Aká je veľkosť vektora?
Veľkosť vektorového vzorca
Smer vektora
Ako nájsť veľkosť vektora?
Vyriešené príklady

Aká je veľkosť vektora?

Veľkosť vektora je definovaná ako dĺžka vektora. Keďže veľkosť vektora označuje dĺžku vektora, je vždy kladná. Pre každý vektor A je jeho veľkosť reprezentovaná ako |A|. Predpokladajme, že vektor je definovaný ako xi + yj, potom jeho veľkosť je definovaná ako druhá odmocnina súčtu druhých mocnín jednotlivých členov. Veľkosť vektora predstavuje dĺžku vektora, t.j. hodnotu alebo vplyv, ktorý má vektor.

Napríklad, ak na objekt pôsobí sila 5i N, jej veľkosť je 5 N, čo znamená, že sila pôsobiacej sily je 5 N, a „ ja' na 5i predstavuje, že sa aplikuje v kladnom smere x.

Veľkosť vektorového vzorca

Existujú rôzne spôsoby výpočtu veľkosti vektora. Na základe daných údajov použite na zistenie veľkosti vektora iný druh vzorca. Veľkosť vektora A je reprezentovaná pomocou modulového operátora, t.j. |A|

Existujú rôzne vzorce, ktoré sa používajú na výpočet veľkosti vektora. Nasledujúci obrázok ukazuje dôležité vzorce používané na zistenie veľkosti vektora.

Nižšie sú uvedené spôsoby výpočtu veľkosti.

Ak im je daný vektor Ā = xi+ yĵ + zk̂, potom veľkosť vektora Ā možno vypočítať pomocou nižšie uvedeného vzorca

Veľkosť vektora Ā (|A|) = √(x ² + a ² +z ² )

Ak je vektor počiatočného bodu povedzme (x₁, a₁) a koncovým bodom vektora je povedzme (x₂, a₂) sú dané potom veľkosťou vektora je daný,

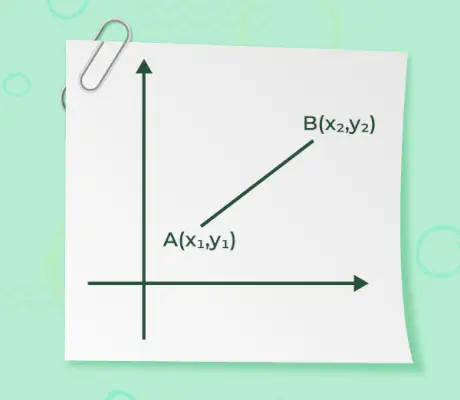
Veľkosť vektora, keď sú zadané počiatočné a koncové body vektora, nie je nič iné ako vzdialenosť medzi bodmi. Vzorec na zistenie magnitúdy je daný podľa

= $sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}$

Ak je niektorý zo začiatočných alebo koncových bodov vektora na začiatku o(0, 0) a iný bod je A(x, y) ako je uvedené na obrázku nižšie,

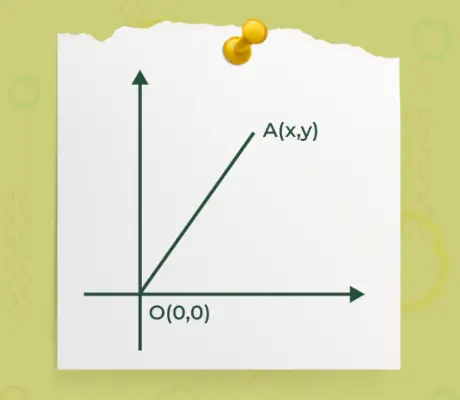
Veľkosť vektora, ak je daný jeden bod a počiatok

Potom vzorec na zistenie veľkosti vektora, kde jeden z koncov vektora je v počiatku, je daný pomocou

|Ā| = √(x ² +y ² )

Smer vektora

Vektorové veličiny sú veličiny, ktoré majú veľkosť aj smer. Smer vektorovej veličiny znamená, ktorým smerom sa vektorová veličina aplikuje. Je definovaný ako uhol, ktorý zviera vektor s vodorovnou čiarou alebo osou x. Je reprezentovaný symbolom a .

Obrázok nižšie ukazuje šípku, ktorá sa používa na zobrazenie smeru vektora.

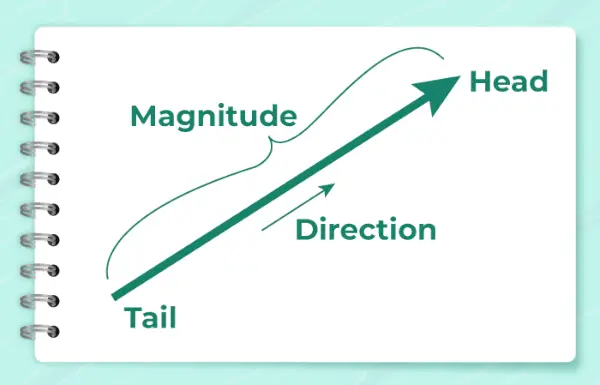
Vypočítava sa pomocou vzorca,

α = opálenie ^-1 (y/x)
: v jave

Pre vektor vygenerovaný súradnicami (x₁, a₁) a (x₂, a₂) ich smer je daný vzorcom,

α = opálenie ^-1 [(a ₂ - a ₁ )/(X ₂ - X ₁ )]

Ako nájsť veľkosť vektora?

Veľkosť vektora sa vypočíta pomocou krokov uvedených nižšie,

Krok 1: Identifikujte zložky x, y a z vektora.

Krok 2 : Nájdite druhú mocninu všetkých komponentov x, y a z.
urobiť skript spustiteľným

Krok 3: Pridajte všetky štvorce nájdené v kroku 2.

Krok 4: Nájdite druhú odmocninu súčtu získaného v kroku 3.

Hodnota získaná po kroku 4 je veľkosť daného vektora.

Príklad: Nájdite veľkosť vektora A = 3i + 4j

Riešenie:

Veľkosť vektora A sa vypočíta pomocou krokov diskutovaných vyššie.

Krok 1: Porovnaním A = 3i + 4j s xi + yj dostaneme x = 3 a y = 4

Krok 2: X²= 3²= 9 a y²= 4²= 16

Krok 3: X²+ a²= 9 + 16 = 25

Krok 4: √(25) = 5

Veľkosť vektora A = 3i + 4j je teda 5 jednotiek.

Záver

Na záver, veľkosť vektora nám hovorí, aký dlhý je vektor. Tento koncept je veľmi dôležitý v mnohých oblastiach, ako je fyzika, inžinierstvo a informatika, pretože pomáha merať veci ako rýchlosť, sila a smer pohybu. Pochopením veľkosti vektora môžeme lepšie analyzovať a riešiť praktické problémy, čo z nich robí kľúčovú časť vedomostí pre každého, kto pracuje s číslami a meraniami v aplikáciách v reálnom svete.

Čítaj viac,

Skalárne a vektorové
Vektorové operácie
Ako vypočítať jednotkový vektor?

Vyriešené príklady veľkosti vektora

Príklad 1: Nájdite veľkosť vektora Ā = 2i + 3ĵ + 4k.

Riešenie:

java reťazec obsahuje

Vzhľadom na to,

Ā = 2i + 3ĵ + 4k

Veľkosť |A| = $sqrt{(2^2+3^2+4^2)}$

=
= √29
= 5,38

Veľkosť vektora 2i+3ĵ+4k je 5.38 jednotka

Príklad 2: Nájdite veľkosť pre vektor Ā = 3i + 3ĵ – 6k

Riešenie:

Dané

Ā = 3i + 3ĵ – 6k

Veľkosť |A| = $sqrt{(3^2+3^2+(-6)^2)}$

=
= √54
= 7,35

Veľkosť vektora 3i+ 3ĵ – 6k je 7.35 jednotka.

Príklad 3: Nájdite veľkosť vektora, ak začiatočný bod vektora je (3, 4) a koncový bod je (6, 2).

Riešenie:

Vzhľadom na to,

(X₁, a₁) = (3, 4)
(X₂, a₂) = (6, 2)

|Ā|= $sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}$

= $sqrt{((6-3)^2+(2-4)^2)}$
= √(3²+ (-2)²)
= √(9+4)
= √13 = 3,6

Veľkosť daného vektora je teda 3.6 jednotka.

Príklad 4: Nájdite veľkosť vektora, ak začiatočný bod vektora je (2, 1, 4) a koncový bod je (5, 2, 6).

Riešenie:

Vzhľadom na to,

(X₁, a₁, S₁) = (2, 1, 4)

(X₂, a₂, S₂) = (5, 2, 6)

|Ā| = $sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}$

= $sqrt{((5-2)^2+(2-1)^2+(6-4)^2)}$
=
= √(9 +1 + 4)
= √14 = 3,74

Veľkosť daného vektora je teda 3,74 jednotka.
java objekt

Príklad 5: Aká je veľkosť vektora, ktorý začína v počiatočnom a koncovom bode v (3, 4).

Riešenie:

Vzhľadom na to,

Počiatočný bod vektora je O(0, 0)

Koncový bod (x, y) = (3, 4)

Veľkosť vektora (|Ā|) = √(x²+y²)

= √(3²+ 4²)
= √(9 + 16)
= √25 = 5

Veľkosť daného vektora je teda 5 jednotka.

Príklad 6: Nájdite veľkosť vektora, v ktorom je jeden z koncových bodov v počiatku a druhý v bode (1, 4, 3).

Riešenie:

Vzhľadom na to,

Koncový bod vektora je O(0, 0)

Iný bod (x, y, z) = (1, 4, 3)

Veľkosť vektora (|Ā|) = √(x²+y²+z²)

= $sqrt{(1^2+4^2+3^2)}$
=
= √26 = 5,09

Veľkosť daného vektora je teda 5.09 jednotka.
rozdiel medzi večerou a večerou

Časté otázky o veľkosti vektora

Aká je veľkosť vektorového vzorca?

Veľkosť vektora je číselná hodnota vektora a určuje dĺžku vektora. Pre každý vektor je jeho veľkosť reprezentovaná ako |A|. Veľkosť vektora sa vypočíta pomocou vzorca,

Pre ľubovoľný vektor A = xi + yj + zk je jeho veľkosť daná vzorcom

|A| = √(x ² + a ² + z ² )

Pre každý vektor, ktorého začiatočný a koncový bod sú (x₁, a₁) a (x₂, a₂) jeho veľkosť je daná vzorcom

|A| = √((x ₂ - X ₁ ) ² + (a ₂ - a ₁ ) ² )

Ako znázorniť veľkosť vektora?

Veľkosť vektora A je reprezentovaný symbolom |A|.

Ako zistiť veľkosť vektora?

Na výpočet veľkosti vektora sa používajú rôzne vzorce, z ktorých niektoré sú,

|A| = √(x ² + a ² + z ² ) keď je vektor v tvare A = xi + yj + zk
|A| = √((x) ² + (a) ² ) keď je vektor daný bodom A (x, y) a počiatkom O(0, 0).
|A| = √((x ₂ - X ₁ ) ² + (a ₂ - a ₁ ) ² ) keď je vektor daný bodom A (x₁, a₂) a bod B (x₂, a₂).

Nájdite vektor veľkosti 5.

Existujú rôzne vektory, ktoré môžu mať veľkosť 5, ktorých príkladom je vektor A reprezentovaný ako,

A = 3i + 4j alebo A = 4i + 5j