NAJNIŽŠÍ SPOLOČNÝ PREDOK V BINÁRNOM STROME - TECHCODEVIEW.COM

Čo je najnižší spoločný predok v binárnom strome?

The najnižší spoločný predok je najnižší uzol v strome, ktorý má n1 aj n2 as potomkovia, kde n1 a n2 sú uzly, pre ktoré chceme nájsť LCA. LCA binárneho stromu s uzlami n1 a n2 je teda spoločným predkom n1 a n2, ktorý sa nachádza najďalej od koreňa.

Aplikácia najnižšieho spoločného predka (LCA):

Na určenie vzdialenosti medzi pármi uzlov v strome: vzdialenosť od n1 do n2 možno vypočítať ako vzdialenosť od koreňa po n1 plus vzdialenosť od koreňa po n2, mínus dvojnásobok vzdialenosti od koreňa po ich najnižší spoločný bod. predok.

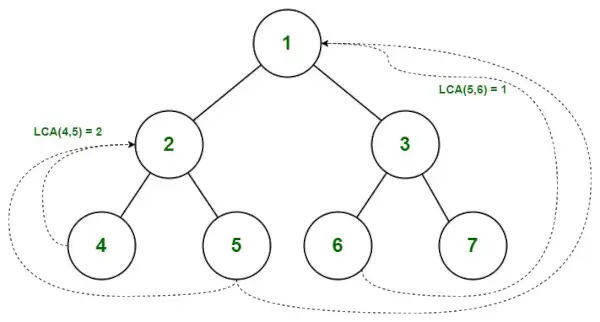
Najnižší spoločný predok v binárnom strome

Odporúčaná prax Najnižší spoločný predok v binárnom strome Vyskúšajte to!

Najnižší spoločný predok v binárnom strome uložením ciest z koreňa do n1 a koreňa do n2:

Myšlienkou tohto prístupu je uložiť cestu od koreňa do n1 a od koreňa do n2 v dvoch samostatných dátových štruktúrach. Potom sa súčasne pozrite na hodnoty uložené v dátovej štruktúre a hľadajte prvý nesúlad.

Ilustrácia:

Nájdite LCA 5 a 6

Cesta od koreňa k 5 = { 1, 2, 5 }
Cesta od koreňa k 6 = { 1, 3, 6 }

Začneme kontrolovať od indexu 0. Keď sa obe hodnoty zhodujú (cestaA[0] = cestaB[0] ), presunieme sa na ďalší index.

cestaA[1] sa nerovná cesteB[1], existuje nesúlad, takže berieme do úvahy predchádzajúcu hodnotu.

Preto LCA (5,6) = 1

Pri riešení problému postupujte podľa nasledujúcich krokov:

Nájdite cestu od koreňa k n1 a uložte ju do vektora alebo poľa.
Nájdite cestu od koreňa k n2 a uložte ju do iného vektora alebo poľa.
Prejdite oboma cestami, kým nebudú hodnoty v poliach rovnaké. Vráťte spoločný prvok tesne pred nezhodou.

Nasleduje implementácia vyššie uvedeného algoritmu:

C++

// C++ Program for Lowest Common Ancestor> // in a Binary Tree> // A O(n) solution to find LCA> // of two given values n1 and n2> #include> using> namespace> std;> // A Binary Tree node> struct> Node {> >int> key;> >struct> Node *left, *right;> };> // Utility function creates a new binary tree node with> // given key> Node* newNode(>int> k)> {> >Node* temp =>new> Node;> >temp->kľúč = k;> >temp->vľavo = teplota->vpravo = NULL;> >return> temp;> }> // Finds the path from root node to given root of the tree,> // Stores the path in a vector path[], returns true if path> // exists otherwise false> bool> findPath(Node* root, vector<>int>>& cesta,>int> k)> (root->vpravo && findPath(root->right, path, k)))> >return> true>;> >// If not present in subtree rooted with root, remove> >// root from path[] and return false> >path.pop_back();> >return> false>;> > // Returns LCA if node n1, n2 are present in the given> // binary tree, otherwise return -1> int> findLCA(Node* root,>int> n1,>int> n2)> > // Driver program to test above functions> int> main()> {> >// Let us create the Binary Tree shown in above diagram.> >Node* root = newNode(1);> >root->left = newNode(2);> >root->vpravo = newNode(3);> >root->left->left = newNode(4);> >root->left->right = newNode(5);> >root->right->left = newNode(6);> >root->right->right = newNode(7);> >cout <<>'LCA(4, 5) = '> << findLCA(root, 4, 5);> >cout <<>

'
LCA(4, 6) = '>

<< findLCA(root, 4, 6);> >cout <<>

'
LCA(3, 4) = '>

<< findLCA(root, 3, 4);> >cout <<>

'
LCA(2, 4) = '>

<< findLCA(root, 2, 4);> >return> 0;> }>

Java

// Java Program for Lowest Common Ancestor> // in a Binary Tree> // A O(n) solution to find LCA of> // two given values n1 and n2> import> java.util.ArrayList;> import> java.util.List;> // A Binary Tree node> class> Node {> >int> data;> >Node left, right;> >Node(>int> value)> >{> >data = value;> >left = right =>null>;> >}> }> public> class> BT_NoParentPtr_Solution1 {> >Node root;> >private> List path1 =>new> ArrayList();> >private> List path2 =>new> ArrayList();> >// Finds the path from root node to given root of the> >// tree.> >int> findLCA(>int> n1,>int> n2)> >{> >path1.clear();> >path2.clear();> >return> findLCAInternal(root, n1, n2);> >}> >private> int> findLCAInternal(Node root,>int> n1,>int> n2)> >{> >if> (!findPath(root, n1, path1)> >|| !findPath(root, n2, path2)) {> >System.out.println((path1.size()>>0>)> >?>'n1 is present'> >:>'n1 is missing'>);> >System.out.println((path2.size()>>0>)> >?>'n2 is present'> >:>'n2 is missing'>);> >return> ->1>;> >}> >int> i;> >for> (i =>0>

; i   i++) {  // System.out.println(path1.get(i) + ' ' +  // path2.get(i));  if (!path1.get(i).equals(path2.get(i)))  break;  }  return path1.get(i - 1);  }  // Finds the path from root node to given root of the  // tree, Stores the path in a vector path[], returns  // true if path exists otherwise false  private boolean findPath(Node root, int n,  List path)  {  // base case  if (root == null) {  return false;  }  // Store this node . The node will be removed if  // not in path from root to n.  path.add(root.data);  if (root.data == n ||  findPath(root.left, n, path) ||  findPath(root.right, n, path)) {  return true;  }  // If not present in subtree rooted with root,  // remove root from path[] and return false  path.remove(path.size() - 1);  return false;  }  // Driver code  public static void main(String[] args)  {  BT_NoParentPtr_Solution1 tree  = new BT_NoParentPtr_Solution1();  tree.root = new Node(1);  tree.root.left = new Node(2);  tree.root.right = new Node(3);  tree.root.left.left = new Node(4);  tree.root.left.right = new Node(5);  tree.root.right.left = new Node(6);  tree.root.right.right = new Node(7);  System.out.println('LCA(4, 5) = '  + tree.findLCA(4, 5));  System.out.println('LCA(4, 6) = '  + tree.findLCA(4, 6));  System.out.println('LCA(3, 4) = '  + tree.findLCA(3, 4));  System.out.println('LCA(2, 4) = '  + tree.findLCA(2, 4));  } } // This code is contributed by Sreenivasulu Rayanki.>

Python3

# Python Program for Lowest Common Ancestor in a Binary Tree> # O(n) solution to find LCS of two given values n1 and n2> # A binary tree node> class> Node:> ># Constructor to create a new binary node> >def> __init__(>self>, key):> >self>.key>=> key> >self>.left>=> None> >self>.right>=> None> # Finds the path from root node to given root of the tree.> # Stores the path in a list path[], returns true if path> # exists otherwise false> def> findPath(root, path, k):> ># Baes Case> >if> root>is> None>:> >return> False> ># Store this node is path vector. The node will be> ># removed if not in path from root to k> >path.append(root.key)> ># See if the k is same as root's key> >if> root.key>=>=> k:> >return> True> ># Check if k is found in left or right sub-tree> >if> ((root.left !>=> None> and> findPath(root.left, path, k))>or> >(root.right !>=> None> and> findPath(root.right, path, k))):> >return> True> ># If not present in subtree rooted with root, remove> ># root from path and return False> >path.pop()> >return> False> # Returns LCA if node n1 , n2 are present in the given> # binary tree otherwise return -1> def> findLCA(root, n1, n2):> ># To store paths to n1 and n2 fromthe root> >path1>=> []> >path2>=> []> ># Find paths from root to n1 and root to n2.> ># If either n1 or n2 is not present , return -1> >if> (>not> findPath(root, path1, n1)>or> not> findPath(root, path2, n2)):> >return> ->1> ># Compare the paths to get the first different value> >i>=> 0> >while>(i <>len>(path1)>and> i <>len>(path2)):> >if> path1[i] !>=> path2[i]:> >break> >i>+>=> 1> >return> path1[i>->1>]> # Driver program to test above function> if> __name__>=>=> '__main__'>:> > ># Let's create the Binary Tree shown in above diagram> >root>=> Node(>1>)> >root.left>=> Node(>2>)> >root.right>=> Node(>3>)> >root.left.left>=> Node(>4>)> >root.left.right>=> Node(>5>)> >root.right.left>=> Node(>6>)> >root.right.right>=> Node(>7>)> > >print>(>'LCA(4, 5) = %d'> %> (findLCA(root,>4>,>5>,)))> >print>(>'LCA(4, 6) = %d'> %> (findLCA(root,>4>,>6>)))> >print>(>'LCA(3, 4) = %d'> %> (findLCA(root,>3>,>4>)))> >print>(>'LCA(2, 4) = %d'> %> (findLCA(root,>2>,>4>)))> # This code is contributed by Nikhil Kumar Singh(nickzuck_007)>

C#

// C# Program for Lowest Common> // Ancestor in a Binary Tree> // A O(n) solution to find LCA> // of two given values n1 and n2> using> System.Collections;> using> System;> // A Binary Tree node> class> Node {> >public> int> data;> >public> Node left, right;> >public> Node(>int> value)> >{> >data = value;> >left = right =>null>;> >}> }> public> class> BT_NoParentPtr_Solution1 {> >Node root;> >private> ArrayList path1 =>new> ArrayList();> >private> ArrayList path2 =>new> ArrayList();> >// Finds the path from root> >// node to given root of the> >// tree.> >int> findLCA(>int> n1,>int> n2)> >{> >path1.Clear();> >path2.Clear();> >return> findLCAInternal(root, n1, n2);> >}> >private> int> findLCAInternal(Node root,>int> n1,>int> n2)> >{> >if> (!findPath(root, n1, path1)> >|| !findPath(root, n2, path2)) {> >Console.Write((path1.Count>0)> >?>'n1 is present'> >:>'n1 is missing'>);> >Console.Write((path2.Count>0)> >?>'n2 is present'> >:>'n2 is missing'>);> >return> -1;> >}> >int> i;> >for>

(i = 0; i   i++) {  // System.out.println(path1.get(i)  // + ' ' + path2.get(i));  if ((int)path1[i] != (int)path2[i])  break;  }  return (int)path1[i - 1];  }  // Finds the path from root node  // to given root of the tree,  // Stores the path in a vector  // path[], returns true if path  // exists otherwise false  private bool findPath(Node root, int n, ArrayList path)  {  // base case  if (root == null) {  return false;  }  // Store this node . The node  // will be removed if not in  // path from root to n.  path.Add(root.data);  if (root.data == n) {  return true;  }  if (root.left != null  && findPath(root.left, n, path)) {  return true;  }  if (root.right != null  && findPath(root.right, n, path)) {  return true;  }  // If not present in subtree  // rooted with root, remove root  // from path[] and return false  path.RemoveAt(path.Count - 1);  return false;  }  // Driver code  public static void Main(String[] args)  {  BT_NoParentPtr_Solution1 tree  = new BT_NoParentPtr_Solution1();  tree.root = new Node(1);  tree.root.left = new Node(2);  tree.root.right = new Node(3);  tree.root.left.left = new Node(4);  tree.root.left.right = new Node(5);  tree.root.right.left = new Node(6);  tree.root.right.right = new Node(7);  Console.Write('LCA(4, 5) = ' + tree.findLCA(4, 5));  Console.Write('
LCA(4, 6) = '  + tree.findLCA(4, 6));  Console.Write('
LCA(3, 4) = '  + tree.findLCA(3, 4));  Console.Write('
LCA(2, 4) = '  + tree.findLCA(2, 4));  } } // This code is contributed by Rutvik_56>

Javascript

> >// JavaScript Program for Lowest Common> >// Ancestor in a Binary Tree> >// A O(n) solution to find LCA of> >// two given values n1 and n2> > >class Node> >{> >constructor(value) {> >this>.left =>null>;> >this>.right =>null>;> >this>.data = value;> >}> >}> > >let root;> >let path1 = [];> >let path2 = [];> > >// Finds the path from root node to given root of the tree.> >function> findLCA(n1, n2) {> >path1 = [];> >path2 = [];> >return> findLCAInternal(root, n1, n2);> >}> > >function> findLCAInternal(root, n1, n2) {> > >if> (!findPath(root, n1, path1) || !findPath(root, n2, path2))> >{> >document.write((path1.length>0) ?> >'n1 is present'> :>'n1 is missing'>);> >document.write((path2.length>0) ?> >'n2 is present'> :>'n2 is missing'>);> >return> -1;> >}> > >let i;> >for>

(i = 0; i     // System.out.println(path1.get(i) + ' ' + path2.get(i));  if (path1[i] != path2[i])  break;  }    return path1[i-1];  }    // Finds the path from root node to   // given root of the tree, Stores the  // path in a vector path[], returns true  // if path exists otherwise false  function findPath(root, n, path)  {  // base case  if (root == null) {  return false;  }    // Store this node . The node will be removed if  // not in path from root to n.  path.push(root.data);    if (root.data == n) {  return true;  }    if (root.left != null && findPath(root.left, n, path)) {  return true;  }    if (root.right != null && findPath(root.right, n, path)) {  return true;  }    // If not present in subtree rooted with root,   // remove root from  // path[] and return false  path.pop();    return false;  }    root = new Node(1);  root.left = new Node(2);  root.right = new Node(3);  root.left.left = new Node(4);  root.left.right = new Node(5);  root.right.left = new Node(6);  root.right.right = new Node(7);  document.write('LCA(4, 5) = ' + findLCA(4,5) + '');  document.write('LCA(4, 6) = ' + findLCA(4,6) + '');  document.write('LCA(3, 4) = ' + findLCA(3,4) + '');  document.write('LCA(2, 4) = ' + findLCA(2,4));>

Výkon

LCA(4, 5) = 2 LCA(4, 6) = 1 LCA(3, 4) = 1 LCA(2, 4) = 2>

Časová zložitosť: O(N). Strom sa prejde dvakrát a potom sa porovnajú polia ciest.
Pomocný priestor: O(N). Extra priestor pre cestu1 a cestu2.

Najnižší spoločný predok v binárnom strome jednoduchým prechodom:

Myšlienkou je prejsť strom začínajúc od koreňa. Ak sa ktorýkoľvek z daných kľúčov (n1 a n2) zhoduje s koreňom, potom je koreň LCA (za predpokladu, že sú prítomné oba kľúče). Ak sa koreň nezhoduje so žiadnym z kľúčov, opakujeme pre ľavý a pravý podstrom.

Uzol, ktorý má jeden kľúč v ľavom podstrome a druhý kľúč v pravom podstrome, je LCA.

Ak oba kľúče ležia v ľavom podstrome, potom ľavý podstrom má tiež LCA,

V opačnom prípade leží LCA v pravom podstrome.

Ilustrácia:

Nájdite LCA 5 a 6

Root ukazuje na uzol s hodnotou 1, pretože jeho hodnota sa nezhoduje s { 5, 6 }. Hľadáme kľúč v ľavom a pravom podstrome.

Ľavý podstrom:

Nový koreň = { 2 } ≠ 5 alebo 6, preto budeme pokračovať v našej rekurzii

Nový koreň = { 4 } , je to ľavý a pravý podstrom je null, pre toto volanie vrátime hodnotu NULL

Nový koreň = { 5 } , hodnota sa zhoduje s 5, takže uzol vráti hodnotu 5

Volanie funkcie pre root s hodnotou 2 vráti hodnotu 5

Pravý podstrom:

Odmocnina = { 3 } ≠ 5 alebo 6, preto pokračujeme v rekurzii

Koreň = { 6 } = 5 alebo 6, vrátime tento uzol s hodnotou 6

Odmocnina = { 7 } ≠ 5 alebo 6, vrátime hodnotu NULL

Takže volanie funkcie pre root s hodnotou 3 vráti uzol s hodnotou 6

Keďže ľavý aj pravý podstrom uzla s hodnotou 1 nie je NULL, tak 1 je LCA

Pri riešení problému postupujte podľa nasledujúcich krokov:

Odošleme koreň pomocnej funkcii a skontrolujeme, či sa hodnota koreňa zhoduje s niektorým z n1 a n2.
- Ak ÁNO, vráťte koreň
- inak rekurzívne volanie na ľavom a pravom podstrome
V podstate robíme prechod predobjednávky, najprv skontrolujeme, či sa root->value zhoduje s n1 alebo n2. Potom prejdite na ľavý a pravý podstrom.
Ak existuje nejaký koreň, ktorý vracia jednu hodnotu NULL a ďalšiu hodnotu NON-NULL, vrátime zodpovedajúcu hodnotu NON-NULL pre tento uzol.
Uzol, ktorý vracia obe hodnoty NON-NULL pre ľavý aj pravý podstrom, je náš najnižší spoločný predok.

Nižšie je uvedená implementácia vyššie uvedeného prístupu.

C++

/* C++ Program to find LCA of n1 and n2 using one traversal> >* of Binary Tree */> #include> using> namespace> std;> // A Binary Tree Node> struct> Node {> >struct> Node *left, *right;> >int> key;> };> // Utility function to create a new tree Node> Node* newNode(>int> key)> {> >Node* temp =>new> Node;> >temp->kľúč = kľúč;> >temp->vľavo = teplota->vpravo = NULL;> >return> temp;> }> // This function returns pointer to LCA of two given values> // n1 and n2. This function assumes that n1 and n2 are> // present in Binary Tree> struct> Node* findLCA(>struct> Node* root,>int> n1,>int> n2)> > >// Base case> >if> (root == NULL)> >return> NULL;> >// If either n1 or n2 matches with root's key, report> >// the presence by returning root (Note that if a key is> >// ancestor of other, then the ancestor key becomes LCA> >if> (root->kľúč == n1> // Driver program to test above functions> int> main()> {> >// Let us create binary tree given in the above example> >Node* root = newNode(1);> >root->left = newNode(2);> >root->vpravo = newNode(3);> >root->left->left = newNode(4);> >root->left->right = newNode(5);> >root->right->left = newNode(6);> >root->right->right = newNode(7);> >cout <<>'LCA(4, 5) = '>

  cout << '
LCA(4, 6) = '   cout << '
LCA(3, 4) = '   cout << '
LCA(2, 4) = '   return 0; } // This code is contributed by Aditya Kumar (adityakumar129)>

C

// C Program to find LCA of n1 and n2 using one traversalof> // Binary Tree> #include> #include> // A Binary Tree Node> typedef> struct> Node {> >struct> Node *left, *right;> >int> key;> } Node;> // Utility function to create a new tree Node> Node* newNode(>int> key)> {> >Node* temp = (Node*)>malloc>(>sizeof>(Node));> >temp->kľúč = kľúč;> >temp->vľavo = teplota->vpravo = NULL;> >return> temp;> }> // This function returns pointer to LCA of two given values> // n1 and n2. This function assumes that n1 and n2 are> // present in Binary Tree> Node* findLCA(Node* root,>int> n1,>int> n2)> > >// Base case> >if> (root == NULL)> >return> NULL;> >// If either n1 or n2 matches with root's key, report> >// the presence by returning root (Note that if a key is> >// ancestor of other, then the ancestor key becomes LCA> >if> (root->kľúč == n1> // Driver program to test above functions> int> main()> {> >// Let us create binary tree given in the above example> >Node* root = newNode(1);> >root->left = newNode(2);> >root->vpravo = newNode(3);> >root->left->left = newNode(4);> >root->left->right = newNode(5);> >root->right->left = newNode(6);> >root->right->right = newNode(7);> >printf>(>'LCA(4, 5) = %d'>, findLCA(root, 4, 5)->kľúč);> >printf>(>

'
LCA(4, 6) = %d'>

, findLCA(root, 4, 6)->kľúč);> >printf>(>

'
LCA(3, 4) = %d'>

, findLCA(root, 3, 4)->kľúč);> >printf>(>

'
LCA(2, 4) = %d'>

, findLCA(root, 2, 4)->kľúč);> >return> 0;> }> // This code is contributed by Aditya Kumar (adityakumar129)>

Java

// Java implementation to find lowest common ancestor of> // n1 and n2 using one traversal of binary tree> /* Class containing left and right child of current> >node and key value*/> class> Node {> >int> data;> >Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> public> class> BinaryTree {> >// Root of the Binary Tree> >Node root;> >Node findLCA(>int> n1,>int> n2)> >{> >return> findLCA(root, n1, n2);> >}> >// This function returns pointer to LCA of two given> >// values n1 and n2. This function assumes that n1 and> >// n2 are present in Binary Tree> >Node findLCA(Node node,>int> n1,>int> n2)> >> >// Base case> >if> (node ==>null>)> >return> null>;> >// If either n1 or n2 matches with root's key,> >// report the presence by returning root (Note that> >// if a key is ancestor of other, then the ancestor> >// key becomes LCA> >if> (node.data == n1> >/* Driver program to test above functions */> >public> static> void> main(String args[])> >{> >BinaryTree tree =>new> BinaryTree();> >tree.root =>new> Node(>1>);> >tree.root.left =>new> Node(>2>);> >tree.root.right =>new> Node(>3>);> >tree.root.left.left =>new> Node(>4>);> >tree.root.left.right =>new> Node(>5>);> >tree.root.right.left =>new> Node(>6>);> >tree.root.right.right =>new> Node(>7>);> >System.out.println(>'LCA(4, 5) = '> >+ tree.findLCA(>4>,>5>).data);> >System.out.println(>'LCA(4, 6) = '> >+ tree.findLCA(>4>,>6>).data);> >System.out.println(>'LCA(3, 4) = '> >+ tree.findLCA(>3>,>4>).data);> >System.out.println(>'LCA(2, 4) = '> >+ tree.findLCA(>2>,>4>).data);> >}> }>

Python3

# Python program to find LCA of n1 and n2 using one> # traversal of Binary tree> # A binary tree node> class> Node:> ># Constructor to create a new tree node> >def> __init__(>self>, key):> >self>.key>=> key> >self>.left>=> None> >self>.right>=> None> # This function returns pointer to LCA of two given> # values n1 and n2> # This function assumes that n1 and n2 are present in> # Binary Tree> def> findLCA(root, n1, n2):> ># Base Case> >if> root>is> None>:> >return> None> ># If either n1 or n2 matches with root's key, report> ># the presence by returning root (Note that if a key is> ># ancestor of other, then the ancestor key becomes LCA> >if> root.key>=>=> n1>or> root.key>=>=> n2:> >return> root> ># Look for keys in left and right subtrees> >left_lca>=> findLCA(root.left, n1, n2)> >right_lca>=> findLCA(root.right, n1, n2)> ># If both of the above calls return Non-NULL, then one key> ># is present in once subtree and other is present in other,> ># So this node is the LCA> >if> left_lca>and> right_lca:> >return> root> ># Otherwise check if left subtree or right subtree is LCA> >return> left_lca>if> left_lca>is> not> None> else> right_lca> # Driver code> if> __name__>=>=> '__main__'>:> > ># Let us create a binary tree given in the above example> >root>=> Node(>1>)> >root.left>=> Node(>2>)> >root.right>=> Node(>3>)> >root.left.left>=> Node(>4>)> >root.left.right>=> Node(>5>)> >root.right.left>=> Node(>6>)> >root.right.right>=> Node(>7>)> >print>(>'LCA(4, 5) = '>, findLCA(root,>4>,>5>).key)> >print>(>'LCA(4, 6) = '>, findLCA(root,>4>,>6>).key)> >print>(>'LCA(3, 4) = '>, findLCA(root,>3>,>4>).key)> >print>(>'LCA(2, 4) = '>, findLCA(root,>2>,>4>).key)> # This code is contributed by Nikhil Kumar Singh(nickzuck_007)>

C#

// C# implementation to find lowest common> // ancestor of n1 and n2 using one traversal> // of binary tree> using> System;> // Class containing left and right> // child of current node and key value> public> class> Node {> >public> int> data;> >public> Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> class> BinaryTree {> >// Root of the Binary Tree> >Node root;> >Node findLCA(>int> n1,>int> n2)> >{> >return> findLCA(root, n1, n2);> >}> >// This function returns pointer to LCA> >// of two given values n1 and n2. This> >// function assumes that n1 and n2 are> >// present in Binary Tree> >Node findLCA(Node node,>int> n1,>int> n2)> > node.data == n2)> >return> node;> >// Look for keys in left and right subtrees> >Node left_lca = findLCA(node.left, n1, n2);> >Node right_lca = findLCA(node.right, n1, n2);> >// If both of the above calls return Non-NULL,> >// then one key is present in once subtree> >// and other is present in other, So this> >// node is the LCA> >if> (left_lca !=>null> && right_lca !=>null>)> >return> node;> >// Otherwise check if left subtree or> >// right subtree is LCA> >return> (left_lca !=>null>) ? left_lca : right_lca;> >> >// Driver code> >public> static> void> Main(>string>[] args)> >{> >BinaryTree tree =>new> BinaryTree();> >tree.root =>new> Node(1);> >tree.root.left =>new> Node(2);> >tree.root.right =>new> Node(3);> >tree.root.left.left =>new> Node(4);> >tree.root.left.right =>new> Node(5);> >tree.root.right.left =>new> Node(6);> >tree.root.right.right =>new> Node(7);> >Console.WriteLine(>'LCA(4, 5) = '> >+ tree.findLCA(4, 5).data);> >Console.WriteLine(>'LCA(4, 6) = '> >+ tree.findLCA(4, 6).data);> >Console.WriteLine(>'LCA(3, 4) = '> >+ tree.findLCA(3, 4).data);> >Console.WriteLine(>'LCA(2, 4) = '> >+ tree.findLCA(2, 4).data);> >}> }> // This code is contributed by pratham76>

Javascript

> >// JavaScript implementation to find> >// lowest common ancestor of> >// n1 and n2 using one traversal of binary tree> > >class Node> >{> >constructor(item) {> >this>.left =>null>;> >this>.right =>null>;> >this>.data = item;> >}> >}> > >//Root of the Binary Tree> >let root;> > >function> findlCA(n1, n2)> >{> >return> findLCA(root, n1, n2);> >}> > >// This function returns pointer to LCA of two given> >// values n1 and n2. This function assumes that n1 and> >// n2 are present in Binary Tree> >function> findLCA(node, n1, n2)> >> > >root =>new> Node(1);> >root.left =>new> Node(2);> >root.right =>new> Node(3);> >root.left.left =>new> Node(4);> >root.left.right =>new> Node(5);> >root.right.left =>new> Node(6);> >root.right.right =>new> Node(7);> >document.write(>'LCA(4, 5) = '> +> >findlCA(4, 5).data +>''>);> >document.write(>'LCA(4, 6) = '> +> >findlCA(4, 6).data +>''>);> >document.write(>'LCA(3, 4) = '> +> >findlCA(3, 4).data +>''>);> >document.write(>'LCA(2, 4) = '> +> >findlCA(2, 4).data +>''>);> > >

Výkon

LCA(4, 5) = 2 LCA(4, 6) = 1 LCA(3, 4) = 1 LCA(2, 4) = 2>

Časová zložitosť : O(N) ako metóda robí jednoduchý prechod stromom zdola nahor.
Pomocný priestor: O(H), kde H je výška stromu.

Poznámka: Vyššie uvedená metóda to predpokladá kľúče sú prítomné v binárnom strome . Ak je jeden kľúč prítomný a druhý chýba, vráti aktuálny kľúč ako LCA (v ideálnom prípade by mal vrátiť hodnotu NULL). Túto metódu môžeme rozšíriť tak, aby zvládla všetky prípady tak, že najprv skontrolujeme, či sú v strome prítomné n1 a n2, a potom nájdeme LCA pre n1 a n2. Ak chcete skontrolovať, či je uzol prítomný v binárnom strome alebo nie, prejdite po strome samostatne pre n1 a n2 uzly.

C++

/* C++ program to find LCA of n1 and n2 using one traversal> >of Binary Tree. It handles all cases even when n1 or n2> >is not there in Binary Tree */> #include> using> namespace> std;> // A Binary Tree Node> struct> Node {> >struct> Node *left, *right;> >int> key;> };> // Utility function to create a new tree Node> Node* newNode(>int> key)> {> >Node* temp =>new> Node;> >temp->kľúč = kľúč;> >temp->vľavo = teplota->vpravo = NULL;> >return> temp;> }> // This function returns pointer to LCA of two given> // valuesn1 and n2.> struct> Node* findLCAUtil(>struct> Node* root,>int> n1,>int> n2)> > // Returns true if key k is present in tree rooted with root> bool> find(Node* root,>int> k)> find(root->vpravo, k))> >return> true>;> >// Else return false> >return> false>;> > // This function returns LCA of n1 and n2 only if both n1> // and n2 are present in tree, otherwise returns NULL;> Node* findLCA(Node* root,>int> n1,>int> n2)> {> >// Return LCA only if both n1 and n2 are present in tree> >if> (find(root, n1) and find(root, n2))> >return> findLCAUtil(root, n1, n2);> >// Else return NULL> >return> NULL;> }> // Driver program to test above functions> int> main()> {> >// Let us create a binary tree given in the above> >// example> >Node* root = newNode(1);> >root->left = newNode(2);> >root->vpravo = newNode(3);> >root->left->left = newNode(4);> >root->left->right = newNode(5);> >root->right->left = newNode(6);> >root->right->right = newNode(7);> >Node* lca = findLCA(root, 4, 5);> >if> (lca != NULL)> >cout <<>'LCA(4, 5) = '>

  else  cout << 'Keys are not present ';  lca = findLCA(root, 4, 10);  if (lca != NULL)  cout << '
LCA(4, 10) = '   else  cout << '
Keys are not present ';  return 0; } // This code is contributed by Kshitij Dwivedi // (kshitijdwivedi28)>

Java

// Java implementation to find lowest common ancestor of> // n1 and n2 using one traversal of binary tree> // It also handles cases even when n1 and n2 are not there> // in Tree> /* Class containing left and right child of current node and> >* key */> class> Node {> >int> data;> >Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> public> class> BinaryTree {> >// Root of the Binary Tree> >Node root;> >static> boolean> v1 =>false>, v2 =>false>;> >// This function returns pointer to LCA of two given> >// values n1 and n2.> >// v1 is set as true by this function if n1 is found> >// v2 is set as true by this function if n2 is found> >Node findLCAUtil(Node node,>int> n1,>int> n2)> >{> >// Base case> >if> (node ==>null>)> >return> null>;> >// Store result in temp, in case of key match so> >// that we can search for other key also.> >Node temp =>null>;> >// If either n1 or n2 matches with root's key,> >// report the presence by setting v1 or v2 as true> >// and return root (Note that if a key is ancestor> >// of other, then the ancestor key becomes LCA)> >if> (node.data == n1) {> >v1 =>true>;> >temp = node;> >}> >if> (node.data == n2) {> >v2 =>true>;> >temp = node;> >}> >// Look for keys in left and right subtrees> >Node left_lca = findLCAUtil(node.left, n1, n2);> >Node right_lca = findLCAUtil(node.right, n1, n2);> >if> (temp !=>null>)> >return> temp;> >// If both of the above calls return Non-NULL, then> >// one key is present in once subtree and other is> >// present in other, So this node is the LCA> >if> (left_lca !=>null> && right_lca !=>null>)> >return> node;> >// Otherwise check if left subtree or right subtree> >// is LCA> >return> (left_lca !=>null>) ? left_lca : right_lca;> >}> >// Finds lca of n1 and n2 under the subtree rooted with> >// 'node'> >Node findLCA(>int> n1,>int> n2)> >{> >// Initialize n1 and n2 as not visited> >v1 =>false>;> >v2 =>false>;> >// Find lca of n1 and n2 using the technique> >// discussed above> >Node lca = findLCAUtil(root, n1, n2);> >// Return LCA only if both n1 and n2 are present in> >// tree> >if> (v1 && v2)> >return> lca;> >// Else return NULL> >return> null>;> >}> >/* Driver program to test above functions */> >public> static> void> main(String args[])> >{> >BinaryTree tree =>new> BinaryTree();> >tree.root =>new> Node(>1>);> >tree.root.left =>new> Node(>2>);> >tree.root.right =>new> Node(>3>);> >tree.root.left.left =>new> Node(>4>);> >tree.root.left.right =>new> Node(>5>);> >tree.root.right.left =>new> Node(>6>);> >tree.root.right.right =>new> Node(>7>);> >Node lca = tree.findLCA(>4>,>5>);> >if> (lca !=>null>)> >System.out.println(>'LCA(4, 5) = '> + lca.data);> >else> >System.out.println(>'Keys are not present'>);> >lca = tree.findLCA(>4>,>10>);> >if> (lca !=>null>)> >System.out.println(>'LCA(4, 10) = '> + lca.data);> >else> >System.out.println(>'Keys are not present'>);> >}> }>

Python3

''' Program to find LCA of n1 and n2 using one traversal of> >Binary tree> It handles all cases even when n1 or n2 is not there in tree> '''> # A binary tree node> class> Node:> ># Constructor to create a new node> >def> __init__(>self>, key):> >self>.key>=> key> >self>.left>=> None> >self>.right>=> None> # This function return pointer to LCA of two given values> # n1 and n2> # v1 is set as true by this function if n1 is found> # v2 is set as true by this function if n2 is found> def> findLCAUtil(root, n1, n2, v):> ># Base Case> >if> root>is> None>:> >return> None> ># IF either n1 or n2 matches ith root's key, report> ># the presence by setting v1 or v2 as true and return> ># root (Note that if a key is ancestor of other, then> ># the ancestor key becomes LCA)> >if> root.key>=>=> n1:> >v[>0>]>=> True> >return> root> >if> root.key>=>=> n2:> >v[>1>]>=> True> >return> root> ># Look for keys in left and right subtree> >left_lca>=> findLCAUtil(root.left, n1, n2, v)> >right_lca>=> findLCAUtil(root.right, n1, n2, v)> ># If both of the above calls return Non-NULL, then one key> ># is present in once subtree and other is present in other,> ># So this node is the LCA> >if> left_lca>and> right_lca:> >return> root> ># Otherwise check if left subtree or right subtree is LCA> >return> left_lca>if> left_lca>is> not> None> else> right_lca> def> find(root, k):> ># Base Case> >if> root>is> None>:> >return> False> ># If key is present at root, or if left subtree or right> ># subtree , return true> >if> (root.key>=>=> k>or> find(root.left, k)>or> >find(root.right, k)):> >return> True> ># Else return false> >return> False> # This function returns LCA of n1 and n2 on value if both> # n1 and n2 are present in tree, otherwise returns None> def> findLCA(root, n1, n2):> ># Initialize n1 and n2 as not visited> >v>=> [>False>,>False>]> ># Find lca of n1 and n2 using the technique discussed above> >lca>=> findLCAUtil(root, n1, n2, v)> ># Returns LCA only if both n1 and n2 are present in tree> >if> (v[>0>]>and> v[>1>]>or> v[>0>]>and> find(lca, n2)>or> v[>1>]>and> >find(lca, n1)):> >return> lca> ># Else return None> >return> None> # Driver program to test above function> root>=> Node(>1>)> root.left>=> Node(>2>)> root.right>=> Node(>3>)> root.left.left>=> Node(>4>)> root.left.right>=> Node(>5>)> root.right.left>=> Node(>6>)> root.right.right>=> Node(>7>)> lca>=> findLCA(root,>4>,>5>)> if> lca>is> not> None>:> >print>(>'LCA(4, 5) = '>, lca.key)> else>:> >print>(>'Keys are not present'>)> lca>=> findLCA(root,>4>,>10>)> if> lca>is> not> None>:> >print>(>'LCA(4,10) = '>, lca.key)> else>:> >print>(>'Keys are not present'>)> # This code is contributed by Nikhil Kumar Singh(nickzuck_007)>

C#

using> System;> // c# implementation to find lowest common ancestor of> // n1 and n2 using one traversal of binary tree> // It also handles cases even when n1 and n2 are not there> // in Tree> /* Class containing left and right child of current node and> >* key */> public> class> Node {> >public> int> data;> >public> Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> public> class> BinaryTree {> >// Root of the Binary Tree> >public> Node root;> >public> static> bool> v1 =>false>, v2 =>false>;> >// This function returns pointer to LCA of two given> >// values n1 and n2.> >// v1 is set as true by this function if n1 is found> >// v2 is set as true by this function if n2 is found> >public> virtual> Node findLCAUtil(Node node,>int> n1,> >int> n2)> >{> >// Base case> >if> (node ==>null>) {> >return> null>;> >}> >// Store result in temp, in case of key match so> >// that we can search for other key also.> >Node temp =>null>;> >// If either n1 or n2 matches with root's key,> >// report the presence by setting v1 or v2 as true> >// and return root (Note that if a key is ancestor> >// of other, then the ancestor key becomes LCA)> >if> (node.data == n1) {> >v1 =>true>;> >temp = node;> >}> >if> (node.data == n2) {> >v2 =>true>;> >temp = node;> >}> >// Look for keys in left and right subtrees> >Node left_lca = findLCAUtil(node.left, n1, n2);> >Node right_lca = findLCAUtil(node.right, n1, n2);> >if> (temp !=>null>) {> >return> temp;> >}> >// If both of the above calls return Non-NULL, then> >// one key is present in once subtree and other is> >// present in other, So this node is the LCA> >if> (left_lca !=>null> && right_lca !=>null>) {> >return> node;> >}> >// Otherwise check if left subtree or right subtree> >// is LCA> >return> (left_lca !=>null>) ? left_lca : right_lca;> >}> >// Finds lca of n1 and n2 under the subtree rooted with> >// 'node'> >public> virtual> Node findLCA(>int> n1,>int> n2)> >{> >// Initialize n1 and n2 as not visited> >v1 =>false>;> >v2 =>false>;> >// Find lca of n1 and n2 using the technique> >// discussed above> >Node lca = findLCAUtil(root, n1, n2);> >// Return LCA only if both n1 and n2 are present in> >// tree> >if> (v1 && v2) {> >return> lca;> >}> >// Else return NULL> >return> null>;> >}> >/* Driver program to test above functions */> >public> static> void> Main(>string>[] args)> >{> >BinaryTree tree =>new> BinaryTree();> >tree.root =>new> Node(1);> >tree.root.left =>new> Node(2);> >tree.root.right =>new> Node(3);> >tree.root.left.left =>new> Node(4);> >tree.root.left.right =>new> Node(5);> >tree.root.right.left =>new> Node(6);> >tree.root.right.right =>new> Node(7);> >Node lca = tree.findLCA(4, 5);> >if> (lca !=>null>) {> >Console.WriteLine(>'LCA(4, 5) = '> + lca.data);> >}> >else> {> >Console.WriteLine(>'Keys are not present'>);> >}> >lca = tree.findLCA(4, 10);> >if> (lca !=>null>) {> >Console.WriteLine(>'LCA(4, 10) = '> + lca.data);> >}> >else> {> >Console.WriteLine(>'Keys are not present'>);> >}> >}> }> // This code is contributed by Shrikant13>

Javascript

> // JavaScript implementation to find lowest> // common ancestor of n1 and n2 using one> // traversal of binary tree. It also handles> // cases even when n1 and n2 are not there in Tree> // Class containing left and right child> // of current node and key> class Node> {> >constructor(item)> >{> >this>.data = item;> >this>.left =>null>;> >this>.right =>null>;> >}> }> class BinaryTree{> > // Root of the Binary Tree> constructor()> {> >this>.root =>null>;> >this>.v1 =>false>;> >this>.v2 =>false>;> }> // This function returns pointer to LCA> // of two given values n1 and n2.> // v1 is set as true by this function> // if n1 is found> // v2 is set as true by this function> // if n2 is found> findLCAUtil(node, n1, n2)> {> > >// Base case> >if> (node ==>null>)> >{> >return> null>;> >}> > >// Store result in temp, in case of> >// key match so that we can search> >// for other key also.> >var> temp =>null>;> > >// If either n1 or n2 matches with root's key,> >// report the presence by setting v1 or v2 as> >// true and return root (Note that if a key> >// is ancestor of other, then the ancestor> >// key becomes LCA)> >if> (node.data == n1)> >{> >this>.v1 =>true>;> >temp = node;> >}> >if> (node.data == n2)> >{> >this>.v2 =>true>;> >temp = node;> >}> > >// Look for keys in left and right subtrees> >var> left_lca =>this>.findLCAUtil(node.left, n1, n2);> >var> right_lca =>this>.findLCAUtil(node.right, n1, n2);> > >if> (temp !=>null>)> >{> >return> temp;> >}> > >// If both of the above calls return Non-NULL,> >// then one key is present in once subtree and> >// other is present in other, So this node is the LCA> >if> (left_lca !=>null> && right_lca !=>null>)> >{> >return> node;> >}> > >// Otherwise check if left subtree or> >// right subtree is LCA> >return> left_lca !=>null> ? left_lca : right_lca;> }> // Finds lca of n1 and n2 under the> // subtree rooted with 'node'> findLCA(n1, n2)> {> > >// Initialize n1 and n2 as not visited> >this>.v1 =>false>;> >this>.v2 =>false>;> > >// Find lca of n1 and n2 using the> >// technique discussed above> >var> lca =>this>.findLCAUtil(>this>.root, n1, n2);> > >// Return LCA only if both n1 and n2> >// are present in tree> >if> (>this>.v1 &&>this>.v2)> >{> >return> lca;> >}> > >// Else return NULL> >return> null>;> }> }> // Driver code> var> tree =>new> BinaryTree();> tree.root =>new> Node(1);> tree.root.left =>new> Node(2);> tree.root.right =>new> Node(3);> tree.root.left.left =>new> Node(4);> tree.root.left.right =>new> Node(5);> tree.root.right.left =>new> Node(6);> tree.root.right.right =>new> Node(7);> var> lca = tree.findLCA(4, 5);> if> (lca !=>null>)> {> >document.write(>'LCA(4, 5) = '> +> >lca.data +>' '>);> }>else> {> >document.write(>'Keys are not present'> +>' '>);> }> lca = tree.findLCA(4, 10);> if> (lca !=>null>)> {> >document.write(>'LCA(4, 10) = '> +> >lca.data +>' '>);> }> else> {> >document.write(>'Keys are not present'> +>' '>);> }> // This code is contributed by rdtank> >

Výkon

LCA(4, 5) = 2 Keys are not present>

Časová zložitosť : O(N) ako metóda robí jednoduchý prechod stromom zdola nahor.
Pomocný priestor: O(H), kde h je výška stromu.

Použitie pomocnej dátovej štruktúry (hashovacia tabuľka):

The basic idea behind the 'Using an auxiliary data structure' approach for finding the lowest common ancestor of two nodes in a binary tree is to use a hash table or a map to store the parent pointers of each node. Once we have the parent pointers, we can traverse up from the first node and add all its ancestors to a set or a list. Then we can traverse up from the second node and check if each ancestor is already in the set or the list. The first ancestor that is already in the set or the list is the lowest common ancestor.>

Postupujte podľa krokov na implementáciu vyššie uvedeného prístupu:

Vytvorte hašovaciu tabuľku alebo mapu na uloženie rodičovských ukazovateľov každého uzla v binárnom strome.
Prejdite binárnym stromom a naplňte hašovaciu tabuľku alebo mapu nadradenými ukazovateľmi pre každý uzol.
Začnite od prvého uzla, prejdite stromom nahor a pridajte každého predka do množiny alebo zoznamu.
Začnite od druhého uzla, prejdite stromom nahor a skontrolujte, či sa každý predok už nenachádza v množine alebo v zozname. Prvý predok, ktorý sa už nachádza v množine alebo zozname, je najnižší spoločný predok.
Ak sa nenájde žiadny spoločný predok, vráťte hodnotu null alebo inú hodnotu, ktorá označuje absenciu spoločného predka.

Nižšie je uvedená implementácia vyššie uvedeného prístupu:

C++

// C++ code to implement above approach> #include> #include> #include> #include> using> namespace> std;> // Definition of a binary tree node> struct> Node {> >int> data;> >Node* left;> >Node* right;> };> // Function to create a new binary tree node> Node* newNode(>int> data)> {> >Node* node =>new> Node;> >node->údaje = údaje;> >node->vľavo = NULL;> >node->vpravo = NULL;> >return> (node);> }> // Function to build a hash table or a map of parent> // pointers for each node in the tree> unordered_map buildParentMap(Node* root)> {> >unordered_map parentMap;> >parentMap[root] = NULL;> >vector queue = { root };> >while> (!queue.empty()) {> >Node* node = queue.front();> >queue.erase(queue.begin());> >if> (node->vľavo) {> >parentMap[node->vľavo] = uzol;> >queue.push_back(node->vľavo);> >}> >if> (node->vpravo) {> >parentMap[node->vpravo] = uzol;> >queue.push_back(node->vpravo);> >}> >}> >return> parentMap;> }> // Function to find the lowest common ancestor of two nodes> // using an auxiliary data structure> int> findLCA(Node* root,>int> n1,>int> n2)> {> >// Build a hash table or a map of parent pointers for> >// each node in the tree> >unordered_map parentMap> >= buildParentMap(root);> >// Find the nodes with values n1 and n2> >Node* p = NULL;> >Node* q = NULL;> >vector queue = { root };> >while> (!queue.empty()) {> >Node* node = queue.front();> >queue.erase(queue.begin());> >if> (node->údaje == n1) {> >p = node;> >}> >if> (node->údaje == n2) {> >q = node;> >}> >if> (node->vľavo) {> >queue.push_back(node->vľavo);> >}> >if> (node->vpravo) {> >queue.push_back(node->vpravo);> >}> >}> >// Add all the ancestors of the first node to a set or a> >// list> >set ancestors;> >while> (p) {> >ancestors.insert(p);> >p = parentMap[p];> >}> >// Traverse up from the second node and check if each> >// ancestor is already in the set or the list> >while> (q) {> >if> (ancestors.find(q) != ancestors.end()) {> >return> q> >->údaje;>// The first ancestor that is> >// already in the set or the list is> >// the lowest common ancestor> >}> >q = parentMap[q];> >}> >return> -1;>// No common ancestor found> }> // Driver code> int> main()> {> >Node* root = newNode(1);> >root->left = newNode(2);> >root->vpravo = newNode(3);> >root->left->left = newNode(4);> >root->left->right = newNode(5);> >root->right->left = newNode(6);> >root->right->right = newNode(7);> >cout <<>'LCA(4, 5) = '> << findLCA(root, 4, 5) << endl;> >cout <<>'LCA(4, 6) = '> << findLCA(root, 4, 6) << endl;> >cout <<>'LCA(3,4) = '> << findLCA(root, 3, 4) << endl;> >cout <<>'LCA(2, 4) = '> << findLCA(root, 2, 4) << endl;> >return> 0;> }> // This code is contributed by Veerendra_Singh_Rajpoot>

Java

import> java.util.*;> // Definition of a binary tree node> class> Node {> >int> data;> >Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> class> Main {> >// Function to build a hash table or a map of parent> >// pointers for each node in the tree> >static> Map buildParentMap(Node root)> >{> >Map parentMap =>new> HashMap();> >parentMap.put(root,>null>);> >Queue queue =>new> LinkedList();> >queue.add(root);> >while> (!queue.isEmpty()) {> >Node node = queue.poll();> >if> (node.left !=>null>) {> >parentMap.put(node.left, node);> >queue.add(node.left);> >}> >if> (node.right !=>null>) {> >parentMap.put(node.right, node);> >queue.add(node.right);> >}> >}> >return> parentMap;> >}> >// Function to find the lowest common ancestor of two> >// nodes using an auxiliary data structure> >static> int> findLCA(Node root,>int> n1,>int> n2)> >{> >// Build a hash table or a map of parent pointers> >// for each node in the tree> >Map parentMap = buildParentMap(root);> >// Find the nodes with values n1 and n2> >Node p =>null>, q =>null>;> >Queue queue =>new> LinkedList();> >queue.add(root);> >while> (!queue.isEmpty()) {> >Node node = queue.poll();> >if> (node.data == n1) {> >p = node;> >}> >if> (node.data == n2) {> >q = node;> >}> >if> (node.left !=>null>) {> >queue.add(node.left);> >}> >if> (node.right !=>null>) {> >queue.add(node.right);> >}> >}> >// Add all the ancestors of the first node to a set> >// or a list> >Set ancestors =>new> HashSet();> >while> (p !=>null>) {> >ancestors.add(p);> >p = parentMap.get(p);> >}> >// Traverse up from the second node and check if> >// each ancestor is already in the set or the list> >while> (q !=>null>) {> >if> (ancestors.contains(q)) {> >return> q.data;> >}> >q = parentMap.get(q);> >}> >return> ->1>;>// No common ancestor found> >}> >public> static> void> main(String[] args)> >{> >Node root =>new> Node(>1>);> >root.left =>new> Node(>2>);> >root.right =>new> Node(>3>);> >root.left.left =>new> Node(>4>);> >root.left.right =>new> Node(>5>);> >root.right.left =>new> Node(>6>);> >root.right.right =>new> Node(>7>);> >System.out.println(>'LCA(4, 5) = '> >+ findLCA(root,>4>,>5>));> >System.out.println(>'LCA(4, 6) = '> >+ findLCA(root,>4>,>6>));> >System.out.println(>'LCA(3, 4) = '> >+ findLCA(root,>3>,>4>));> >System.out.println(>'LCA(3, 4) = '> >+ findLCA(root,>2>,>4>));> >}> }>

Python3

from> collections>import> deque> # Definition of a binary tree node> class> Node:> >def> __init__(>self>, data):> >self>.data>=> data> >self>.left>=> None> >self>.right>=> None> # Function to build a hash table or a map of parent> # pointers for each node in the tree> def> buildParentMap(root):> >parentMap>=> {}> >parentMap[root]>=> None> >queue>=> deque([root])> >while> queue:> >node>=> queue.popleft()> >if> node.left:> >parentMap[node.left]>=> node> >queue.append(node.left)> >if> node.right:> >parentMap[node.right]>=> node> >queue.append(node.right)> >return> parentMap> # Function to find the lowest common ancestor of two nodes> # using an auxiliary data structure> def> findLCA(root, n1, n2):> ># Build a hash table or a map of parent pointers for> ># each node in the tree> >parentMap>=> buildParentMap(root)> ># Find the nodes with values n1 and n2> >p, q>=> None>,>None> >queue>=> deque([root])> >while> queue:> >node>=> queue.popleft()> >if> node.data>=>=> n1:> >p>=> node> >if> node.data>=>=> n2:> >q>=> node> >if> node.left:> >queue.append(node.left)> >if> node.right:> >queue.append(node.right)> ># Add all the ancestors of the first node to a set or a> ># list> >ancestors>=> set>()> >while> p:> >ancestors.add(p)> >p>=> parentMap[p]> ># Traverse up from the second node and check if each> ># ancestor is already in the set or the list> >while> q:> >if> q>in> ancestors:> >return> q.data> >q>=> parentMap[q]> >return> ->1> # No common ancestor found> # Driver code> if> __name__>=>=> '__main__'>:> >root>=> Node(>1>)> >root.left>=> Node(>2>)> >root.right>=> Node(>3>)> >root.left.left>=> Node(>4>)> >root.left.right>=> Node(>5>)> >root.right.left>=> Node(>6>)> >root.right.right>=> Node(>7>)> >print>(>'LCA(4, 5) = '>, findLCA(root,>4>,>5>))> >print>(>'LCA(4, 6) = '>, findLCA(root,>4>,>6>))> >print>(>'LCA(3, 4) = '>, findLCA(root,>3>,>4>))> >print>(>'LCA(2, 4) = '>, findLCA(root,>2>,>4>))>

C#

using> System;> using> System.Collections.Generic;> // Definition of a binary tree node> class> Node> {> >public> int> data;> >public> Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> class> MainClass> {> >// Function to build a hash table or a map of parent> >// pointers for each node in the tree> >static> Dictionary BuildParentMap(Node root)> >{> >Dictionary parentMap =>new> Dictionary();> >parentMap.Add(root,>null>);> >Queue queue =>new> Queue();> >queue.Enqueue(root);> >while> (queue.Count != 0)> >{> >Node node = queue.Dequeue();> >if> (node.left !=>null>)> >{> >parentMap.Add(node.left, node);> >queue.Enqueue(node.left);> >}> >if> (node.right !=>null>)> >{> >parentMap.Add(node.right, node);> >queue.Enqueue(node.right);> >}> >}> >return> parentMap;> >}> >// Function to find the lowest common ancestor of two> >// nodes using an auxiliary data structure> >static> int> FindLCA(Node root,>int> n1,>int> n2)> >{> >// Build a hash table or a map of parent pointers> >// for each node in the tree> >Dictionary parentMap = BuildParentMap(root);> >// Find the nodes with values n1 and n2> >Node p =>null>, q =>null>;> >Queue queue =>new> Queue();> >queue.Enqueue(root);> >while> (queue.Count != 0)> >{> >Node node = queue.Dequeue();> >if> (node.data == n1)> >{> >p = node;> >}> >if> (node.data == n2)> >{> >q = node;> >}> >if> (node.left !=>null>)> >{> >queue.Enqueue(node.left);> >}> >if> (node.right !=>null>)> >{> >queue.Enqueue(node.right);> >}> >}> >// Add all the ancestors of the first node to a set> >// or a list> >HashSet ancestors =>new> HashSet();> >while> (p !=>null>)> >{> >ancestors.Add(p);> >p = parentMap[p];> >}> >// Traverse up from the second node and check if> >// each ancestor is already in the set or the list> >while> (q !=>null>)> >{> >if> (ancestors.Contains(q))> >{> >return> q.data;> >}> >q = parentMap[q];> >}> >return> -1;>// No common ancestor found> >}> >public> static> void> Main()> >{> >Node root =>new> Node(1);> >root.left =>new> Node(2);> >root.right =>new> Node(3);> >root.left.left =>new> Node(4);> >root.left.right =>new> Node(5);> >root.right.left =>new> Node(6);> >root.right.right =>new> Node(7);> >Console.WriteLine(>'LCA(4, 5) = '> + FindLCA(root, 4, 5));> >Console.WriteLine(>'LCA(4, 6) = '> + FindLCA(root, 4, 6));> >Console.WriteLine(>'LCA(3, 4) = '> + FindLCA(root, 3, 4));> >Console.WriteLine(>'LCA(2, 4) = '> + FindLCA(root, 2, 4));> >}> }> // This code is contributed by akashish__>

Javascript

// javascript code addition> // Definition of a binary tree node> class Node {> >constructor(item) {> >this>.data = item;> >this>.left =>null>;> >this>.right =>null>;> >}> }> // Function to build a hash table or a map of parent> // pointers for each node in the tree> function> buildParentMap(root) {> >const parentMap =>new> Map();> >parentMap.set(root,>null>);> >const queue = [];> >queue.push(root);> >while> (queue.length>0) {> >const node = queue.shift();> >if> (node.left !=>null>) {> >parentMap.set(node.left, node);> >queue.push(node.left);> >}> >if> (node.right !=>null>) {> >parentMap.set(node.right, node);> >queue.push(node.right);> >}> >}> >return> parentMap;> }> // Function to find the lowest common ancestor of two> // nodes using an auxiliary data structure> function> findLCA(root, n1, n2) {> >// Build a hash table or a map of parent pointers> >// for each node in the tree> >const parentMap = buildParentMap(root);> >// Find the nodes with values n1 and n2> >let p =>null>, q =>null>;> >const queue = [];> >queue.push(root);> >while> (queue.length>0) {> >const node = queue.shift();> >if> (node.data === n1) {> >p = node;> >}> >if> (node.data === n2) {> >q = node;> >}> >if> (node.left !=>null>) {> >queue.push(node.left);> >}> >if> (node.right !=>null>) {> >queue.push(node.right);> >}> >}> >// Add all the ancestors of the first node to a set> >// or a list> >const ancestors =>new> Set();> >while> (p !=>null>) {> >ancestors.add(p);> >p = parentMap.get(p);> >}> >// Traverse up from the second node and check if> >// each ancestor is already in the set or the list> >while> (q !=>null>) {> >if> (ancestors.has(q)) {> >return> q.data;> >}> >q = parentMap.get(q);> >}> >return> -1;>// No common ancestor found> }> // Test the function> const root =>new> Node(1);> root.left =>new> Node(2);> root.right =>new> Node(3);> root.left.left =>new> Node(4);> root.left.right =>new> Node(5);> root.right.left =>new> Node(6);> root.right.right =>new> Node(7);> console.log(>'LCA(4, 5) = '> + findLCA(root, 4, 5));> console.log(>'LCA(4, 6) = '> + findLCA(root, 4, 6));> console.log(>'LCA(3, 4) = '> + findLCA(root, 3, 4));> console.log(>'LCA(2, 4) = '> + findLCA(root, 2, 4));> // The code is contributed by Nidhi goel.>

Výkon

LCA(4, 5) = 2 LCA(4, 6) = 1 LCA(3,4) = 1 LCA(2, 4) = 2>

Časová zložitosť: O(n),

ako previesť str na int

Časová zložitosť daného kódu je O(n), kde n je počet uzlov v binárnom strome.

Vytvorenie rodičovskej mapy pre každý uzol v strome vyžaduje návštevu každého uzla raz, čo zaberie O(n) čas. Nájdenie uzlov s hodnotami n1 a n2 vyžaduje návštevu každého uzla raz, čo tiež trvá O(n) čas. Prechod nahor z druhého uzla a kontrola, či je každý predok už v množine alebo v zozname, trvá O(h) čas, kde h je výška binárneho stromu.

V najhoršom prípade je výška binárneho stromu O(n), ak je binárny strom zošikmený. Celková časová zložitosť daného kódu je teda O(n) + O(n) + O(n) = O(n).

Priestorová zložitosť: O(n),

Priestorová zložitosť daného kódu je v najhoršom prípade O(n). Je to preto, že veľkosť rodičovskej mapy zostavenej pre každý uzol v strome je O(n). Okrem toho môže množina predkov obsahovať aj všetky uzly v binárnom strome v najhoršom prípade, ktorý tiež zaberá O(n) priestor. Nakoniec, front používaný na prechádzanie binárnym stromom zaberá O(n) miesta. Celková priestorová zložitosť daného kódu je teda O(n) + O(n) + O(n) = O(n).

Diskutovali sme o efektívnom riešení na nájdenie LCA v binárnom vyhľadávacom strome. V binárnom vyhľadávacom strome pomocou vlastností BST môžeme nájsť LCA v čase O(h), kde h je výška stromu. Takáto implementácia nie je možná v binárnom strome, pretože kľúče uzlov binárneho stromu nesledujú žiadne poradie.

Možno by ste si chceli pozrieť aj nižšie uvedené články:
LCA pomocou nadradeného ukazovateľa
Najnižší spoločný predok v binárnom vyhľadávacom strome.
Nájdite LCA v binárnom strome pomocou RMQ