A Riadený acyklický graf , často skracované ako DAY , je základným pojmom v teórii grafov. DAG's sa používajú na to, aby jasne a organizovane ukázali, ako veci spolu súvisia alebo na sebe závisia. V tomto článku sa dozvieme o Riadený acyklický graf , jeho vlastnosti a uplatnenie v reálnom živote.

Riadený acyklický graf

Čo je to riadený acyklický graf?

A Riadený acyklický graf (DAG) je orientovaný graf, ktorý neobsahuje žiadne cykly.

Nižšie uvedený graf predstavuje riadený acyklický graf (DAG):

Priamy acyklický graf

Význam smerovaného acyklického grafu:

Riadený acyklický graf má dve dôležité vlastnosti:

• Riadený okraj s:V riadenom acyklickom grafe každá hrana má smer, čo znamená, že ide z jedného vrcholu (uzla) do druhého. Tento smer znamená a jednosmerka vzťah alebo závislosť medzi uzlami.
• Acyklické: Termín acyklický označuje, že v grafe nie sú žiadne cykly ani uzavreté slučky. Inými slovami, nemôžete prejsť sekvenciou nasmerovaných hrán a vrátiť sa do rovnakého uzla podľa smerov hrán. Vytváranie cyklov je zakázané DAY. Preto je táto vlastnosť nevyhnutná.

Riadený acyklický graf

Vlastnosti riadeného acyklického grafu DAG:

Riadený acyklický graf (DAG) má rôzne vlastnosti, vďaka ktorým sú použiteľné v problémoch s grafmi.

Smerovaný acyklický graf (DAG) má nasledujúce vlastnosti:

• Vzťah k dosiahnuteľnosti: V DAG môžeme určiť, či existuje vzťah dosiahnuteľnosti medzi dvoma uzlami. O uzle A sa hovorí, že je dosiahnuteľný z uzla B, ak existuje smerovaná cesta, ktorá začína v uzle B a končí v uzle A. To znamená, že môžete sledovať smer hrán v grafe, aby ste sa dostali z B do A.
• Tranzitná uzávierka: Tranzitívny uzáver orientovaného grafu je nový graf, ktorý predstavuje všetky priame a nepriame vzťahy alebo spojenia medzi uzlami v pôvodnom grafe. Inými slovami, povie vám, ktoré uzly možno dosiahnuť z iných uzlov sledovaním jednej alebo viacerých smerovaných hrán.

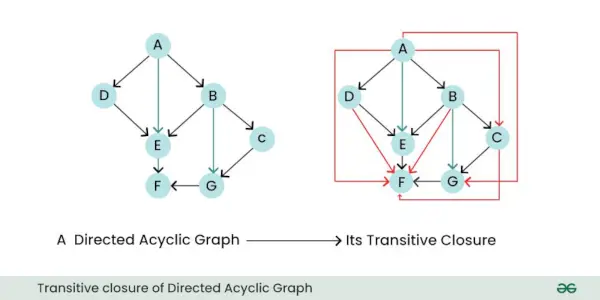
Tranzitívne uzavretie riadeného acyklického grafu

• Tranzitívna redukcia: Tranzitívna redukcia orientovaného grafu je nový graf, ktorý zachováva iba podstatné, priame vzťahy medzi uzlami, pričom odstraňuje všetky zbytočné nepriame hrany. V podstate zjednodušuje graf odstránením hrán, ktoré možno odvodiť zo zostávajúcich hrán.

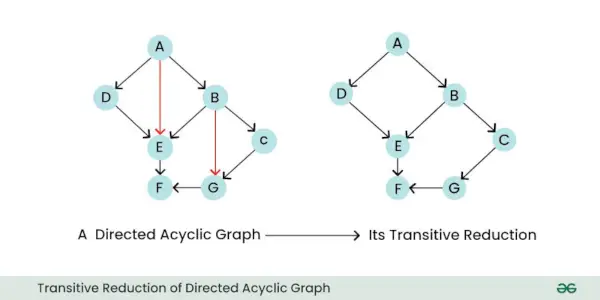
Tranzitívna redukcia riadeného acyklického grafu

• Topologické usporiadanie: DAG je možné topologicky triediť, čo znamená, že môžete lineárne usporiadať jeho uzly takým spôsobom, že pre všetky hrany sa počiatočný uzol hrany vyskytuje skôr v sekvencii. Táto vlastnosť je užitočná pre úlohy, ako je plánovanie a riešenie závislostí.

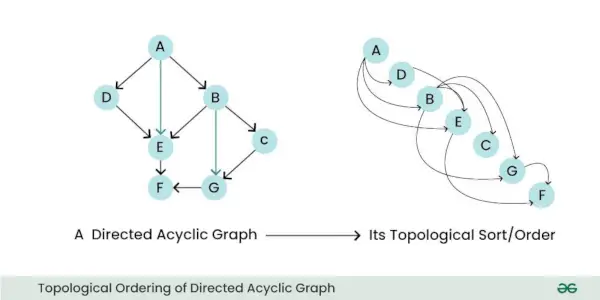
Topologické usporiadanie riadeného acyklického grafu

Praktické aplikácie DAG:

• Analýza toku údajov: Pri návrhu a optimalizácii kompilátora sa DAG používajú na reprezentáciu toku údajov v rámci programu. To pomáha pri optimalizácii kódu identifikáciou nadbytočných výpočtov a mŕtveho kódu. DAG sa tiež používajú na znázornenie štruktúry základné bloky v dizajne kompilátora.

• Plánovanie úloh: DAG sa používajú pri riadení projektov a plánovaní úloh. Každá úloha alebo úloha je reprezentovaná ako uzol v DAG, s nasmerovanými okrajmi označujúcimi závislosti. Acyklická povaha DAG zabezpečuje, že úlohy sú naplánované v logickom poradí, čím sa predchádza kruhovým závislostiam.

Na znázornenie problému plánovania možno použiť vážený orientovaný acyklický graf. Vezmime si príklad problému s plánovaním úloh. V tomto prípade môže vrchol reprezentovať úlohu a jeho váha môže predstavovať veľkosť výpočtu úlohy. Podobne hrana môže predstavovať komunikáciu medzi dvoma úlohami a jej váha môže predstavovať náklady na komunikáciu:

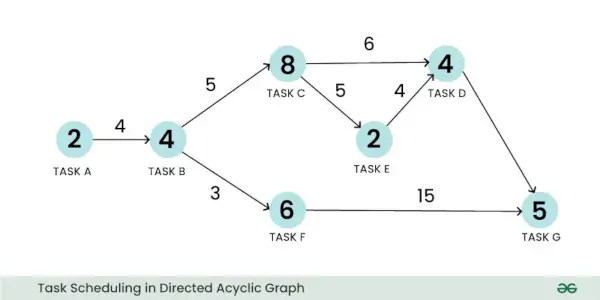
Plánovanie úloh v riadenom acyklickom grafe

Záver:

Stručne povedané, riadené acyklické grafy sú základným konceptom teórie grafov s mnohými praktickými aplikáciami. DAG hrajú kľúčovú úlohu pri plánovaní úloh, analýze toku údajov, riešení závislostí a rôznych ďalších oblastiach informatiky a inžinierstva. Pomáhajú optimalizovať procesy, riadiť závislosti a zabezpečiť efektívne vykonávanie úloh alebo úloh.