Stred trojuholníka je priesečník všetkých troch uhlových osi trojuholníka. Stred je dôležitým bodom v trojuholníku, kde sa spájajú čiary zrezané na polovicu. Tento bod je tiež stredom kruhu nazývaného Incircle, ktorý dokonale zapadá do trojuholníka a dotýka sa všetkých troch strán rovnako. Tento článok sa zaoberá rôznymi konceptmi stredu trojuholníka, napríklad prečo je tento bod dôležitý, ako ho nájsť pomocou kompasu alebo čísel a vlastnosti stredu kruhu.

Obsah

• Čo je stred trojuholníka?
• Vlastnosti stredu trojuholníka
• Stred trojuholníkového vzorca
• Ako nájsť stred trojuholníka
• Centroid, Circumcenter, Incenter, Orthocenter

Čo je stred trojuholníka?

Stred trojuholníka, ako už názov napovedá, je stredom trojuholníka. Tento bod, ktorý nazývame stred, sa tvorí na križovatke, kde sa stretávajú všetky čiary, ktoré pretínajú vnútorné uhly. Vzdialenosť bodu od všetkých troch strán trojuholníka je rovnaká. Kružnica trojuholníka tiež zapadá do dokonalého kruhu vo vnútri trojuholníka a tento kruh sa nazýva kruh trojuholníka.

Definícia stredu

Stred trojuholníka je bod vo vnútri trojuholníka, kde sa spájajú všetky tri čiary, ktoré pretínajú jeho vnútorné uhly na polovicu. Tento bod je v rovnakej vzdialenosti od troch strán trojuholníka, takže je ako stred trojuholníka. Je to tiež stred najväčšieho kruhu, ktorý sa zmestí do trojuholníka, ktorý nazývame kruhový kruh. Na symbolizáciu stredu zvyčajne používame písmeno I,

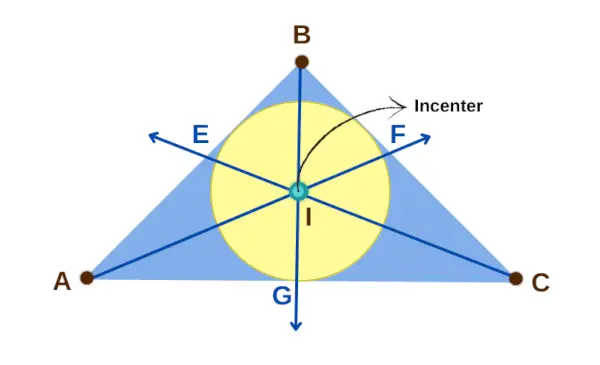
Stred trojuholníka

Vlastnosti stredu trojuholníka

Niektoré dôležité vlastnosti stredu trojuholníka sú uvedené nižšie:

Vlastnosť 1: Ak ja je stred trojuholníka ABC, potom majú tri páry úsečiek rovnakú dĺžku: AE a AG, CG a CF a BF a BE. To znamená, že AE = AG, CG = CF a BF = BE.

Vlastnosť 2: Stredisko ja má tiež špeciálny vzťah s uhlami trojuholníka. Spôsobuje, že uhly ∠BAI a ∠CAI sú rovnaké, ∠BCI a ∠ACI sú rovnaké a ∠ABI a ∠CBI sú rovnaké. Nasleduje veta o uhlovej osi.

Vlastnosť 3: Stredisko ja je stred kruhu, ktorý sa dotýka všetkých troch strán trojuholníka, a vzdialenosti od ja do strán trojuholníka (EI, FI, GI) sú všetky rovnaké. Tieto vzdialenosti sa nazývajú polomery alebo polomer kružnice.

Vlastnosť 4: Plochu trojuholníka môžete vypočítať pomocou semiperimetra (s) a polomeru (r). Vzorec je A = sr, kde A je plocha, s je semiperimeter (s = (a + b + c)/2, kde a, b a c sú dĺžky strán trojuholníka) a r je polomer.

Vlastnosť 5: Stred trojuholníka vždy zostáva vo vnútri trojuholníka. Na rozdiel od ortocentra, ktoré môže byť v niektorých prípadoch mimo trojuholníka, je centrum vždy obsiahnuté v hraniciach trojuholníka.

Stred trojuholníkového vzorca

Vzorec na nájdenie stredu vzorca s 3 súradnicami (x₁, a₁), (X₂, a₂) a (x₃, a₃) je:

{(ax ₁ + bx ₂ + cx ₃ )/(a + b + c), (je ₁ + podľa ₂ + c ₃ )/(a + b + c)}

Jednoducho povedané, ak chcete získať centrum, musíte:

• Vynásobte x-ovú súradnicu bodu A dĺžkou strany a, x-ovú súradnicu bodu B dĺžkou strany b a x-ovú súradnicu bodu C dĺžkou strany c. Potom ich pridajte spolu.
• Výsledok vydeľte súčtom dĺžok strán a, b a c.
• Opakujte rovnaký postup pre y-ové súradnice, ale s použitím dĺžok strán a, b a c.

Vzorec stredu trojuholníka

Vzorec na nájdenie stredu uhla trojuholníka je nasledujúci:

V trojuholníku D, F a G sú body, v ktorých sa osi uhla uhlov A, B a C stretávajú so stranami BC, AC a AB.

Uhol ∠AIB (kde I je stred trojuholníka) možno vypočítať pomocou vzorca:

∠AIB = 180° – (polovica súčtu uhlov A a B)

ALEBO

∠AIB = 180° – (∠A + ∠B)/2

Ako nájsť stred trojuholníka

Existujú dva spôsoby, ako nájsť stred trojuholníka. Pri konštrukcii lokalizujeme stred tak, že nakreslíme osy uhla trojuholníka. V geometrii súradníc používame vzorec na určenie stredu.

Použitie súradnicovej geometrie : Nájdite stred trojuholníka so súradnicami uvedenými ako: A(2, 2), B(6, 2) a C(4, 5)

príklad podreťazca java

Podľa uvedených informácií

• (X₁, a₁) = (2, 2)
• (X₂, a₂) = (6, 2)
• (X₃, a₃) = (4, 5)

Vieme, že stred trojuholníka je:

I(x, y) = {(ax ₁ + bx ₂ + cx ₃ )/(a + b + c), (je ₁ + podľa ₂ + c ₃ )/(a + b + c)}

Pre stranu a: Vzdialenosť medzi bodmi B a C = √((6 – 4)²+ (2 – 5)²) = √8

Pre stranu b: Vzdialenosť medzi bodmi A a C = √((2 – 4)²+ (2 – 5)²) = √13

Pre stranu c: Vzdialenosť medzi bodmi A a B = √((6 – 2)²+ (2 – 2)²) = 4

Vložením hodnôt a, b, c do vzorca stredu dostaneme:

I(x, y) = {(8×2 + 13×5 + 4×4)/(8 + 13 +4), (8×2 + 13×2 + 4×5)/(8 + 13 +4 )}

⇒ I(x, y) = (16 + 78 + 16)/(25), (16 + 26 + 20)/(25)

⇒ I(x, y) = (110/25, 62/25) = (22/5,62/25)

∴ Stred trojuholníka ABC so súradnicami je (22/5,62/25)

Ako postaviť stred trojuholníka?

Na vytvorenie stredu trojuholníka bude potrebné použiť kompas. Pri použití kompasu postupujte podľa nižšie uvedených krokov:

Krok 1: Jeden koniec kružidla položte na vrchol trojuholníka a druhý koniec sa dotýka jednej strany.

Krok 2: Pomocou kružidla nakreslite dva oblúky na dve strany trojuholníka.

Krok 3: S rovnakou vzdialenosťou na kompase urobte dva oblúky vo vnútri trojuholníka. Tieto oblúky by sa mali navzájom pretínať z miesta, kde sa dotýkajú strán.

Krok 4: Nakreslite čiaru od vrcholu trojuholníka k miestu, kde sa pretínajú dva vnútorné oblúky.

Krok 5: Opakujte rovnaké kroky z druhého vrcholu trojuholníka.

Krok 6: Miesto, kde sa tieto dve čiary stretávajú alebo krížia, je stred trojuholníka.

Stred pravouhlého trojuholníka

Stred, ak a Pravouhlý trojuholník je bod, v ktorom sa stretávajú všetky osi pravouhlého trojuholníka. Ak strany pravouhlého trojuholníka merajú a, b a c, potom polomer kružnice „r“ je daný ako r = (ab)/(a + b + c). Stred pravého trojuholníka je znázornený nižšie:

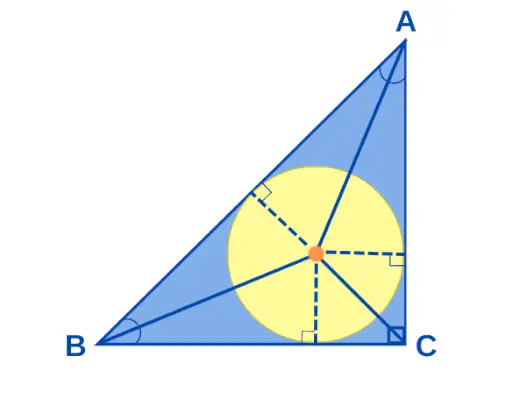
Stred pravouhlého trojuholníka

Centroid, Circumcenter, Incenter, Orthocenter

Centroid, Circumcenter, Incenter a Orthocenter sú štyri dôležité body súvisiace s traingle. Porovnanie medzi Centroidom, Circumcenter, Incenter a Orthocenter je uvedené v tabuľke nižšie:

Tiež skontrolujte

• Oblasť trojuholníka
• Obvod trojuholníka
• Vlastnosť súčtu uhla trojuholníka

Príklady stredu trojuholníka

Príklad 1: Vypočítajte stred trojuholníka ABC. AB = 8 cm, BC = 15 cm, CA = 17 cm.

Riešenie:

Pomocou vzorca Stred trojuholníka = (aA + bB + cC)/(a + b + c)

kde,

• a = 8
• b = 15
• c = 17

A uhly sú,

• A = 30°
• B = 60°
• C = 90 °C

Uvedením týchto hodnôt do vzorca získate,

⇒ {(8)(30) + (15)(60) + (17)(90)}/{8 + 15 + 17}

⇒ (240 + 900 + 1530)/40

⇒ 2670/40

⇒ 66,75

Príklad 2: Jane vypočítala plochu trojuholníkového poľa ako 120 metrov štvorcových. Obvod ihriska je 36 metrov. Ak je vo vnútri trojuholníka nakreslený kruh tak, že sa dotýka každej strany trojuholníka, pomôžte Jane vypočítať polomer trojuholníka.

cast string to int

Riešenie:

Podľa uvedených informácií

Plocha trojuholníka = 120 metrov štvorcových

Obvod trojuholníka = 36 metrov

Vieme, že plocha trojuholníka = r × s

s = semiperimeter

s = p/2 = 36/2 = 18

A = r × s

r = A/s

r = 120/18

r = 6,67 metra

Cvičné problémy v strede trojuholníka

Úloha 1: Daný trojuholník PQR s vrcholmi P(1, 2), Q(4, 6) a R(7, 2) nájdite súradnice stredu.

Úloha 2: Zostrojte trojuholník ABC s ∠A = 45°, ∠B = 60° a ∠C = 75°. Pomocou konštrukčnej metódy nájdite stred.

Úloha 3: V trojuholníku LMN, ak ∠L = 75°, ∠M = 60° a ∠N = 45°, nájdite súradnice stredu.

Úloha 4: Zostrojte trojuholník XYZ s ∠X = 80°, ∠Y = 50° a ∠Z = 50°. Pomocou konštrukčnej metódy nájdite stred.

Stred trojuholníka: často kladené otázky

Čo je stred trojuholníka?

Stred trojuholníka je bod, kde sa pretínajú osy vnútorných uhlov. Je rovnako vzdialený od všetkých troch strán trojuholníka.

Aký je význam stredu v trojuholníku?

Stred je významný, pretože je stredom kruhu trojuholníka, najväčšieho kruhu, ktorý sa zmestí do trojuholníka. Má tú vlastnosť, že je zo všetkých strán rovnako vzdialený.

Môže byť Incent mimo trojuholníka?

Nie, stred je vždy vnútri trojuholníka. Je to bod súbežnosti pre osi uhla a podľa definície musí byť v rámci hraníc trojuholníka.

Ako sa tvorí stred pomocou kružidla a rovného okraja?

Ak chcete zostrojiť stred, použite kružidlo na nakreslenie osi uhla z každého vrcholu na opačnú stranu. Stred je bod, kde sa tieto priesečníky pretínajú.

Čo je Incenter Formula?

Vzorec pre Stred trojuholníka možno napísať takto:

frac{(aA+bB+cC)}{a+b+c}

Aké sú vlastnosti stredu trojuholníka?

Incenter má niektoré kľúčové vlastnosti. Je rovnako vzdialený od strán trojuholníka, čo znamená, že vzdialenosti medzi stranami sú rovnaké. Je to tiež priesečník osi uhla, ktorý rozdeľuje uhly na dve rovnaké časti.

Ako sa určuje stred?

Ak chcete určiť stred, musíte nájsť miesto, kde sa pretínajú osi uhla. Dá sa to urobiť pomocou stredového vzorca alebo nakreslením osí uhla a nájdením ich priesečníka.

Aký je rozdiel medzi Incentre a Circumcentre?

Hlavným rozdielom medzi incenter a circumcenter je ich zameranie. Stred sa zaoberá stredom osí uhla a je stredom opísanej kružnice, zatiaľ čo stred opísanej kružnice sa zaoberá kolmými osami a je stredom opísanej kružnice.

Je Incentre a Centroid to isté?

Nie, stred a ťažisko sú odlišné. Stred je miesto, kde sa stretávajú osi uhla, zatiaľ čo ťažisko je miesto, kde sa pretínajú stredy. Mediány spájajú vrcholy so stredom opačnej strany.

Je Incentre a Ortocentre to isté?

Nie, incentrum a ortocentrum nie sú to isté. Stred je bod, kde sa uhol vzájomne pretína, zatiaľ čo ortocentrum zahŕňa nadmorské výšky – čiary z každého vrcholu kolmé na opačnú stranu. Sú to rôzne body v trojuholníku.