Horizontálne čiary sú definované ako čiary, ktoré sú rovnobežné s horizontom alebo zemou, preto sa nazýva horizontálna čiara . Vodorovná čiara má nulový sklon, t.j. uhol sklonu týchto čiar je nula stupňov. Ak sú vodorovné čiary nakreslené na karteziánskych rovinách, zasahujú iba pozdĺž osi y, pretože sú vždy rovnobežné s osou x a nikdy ju nepretínajú.
V tomto článku sa podrobne dozvieme o vodorovnej čiare, jej vlastnostiach, sklone vodorovnej čiary, rovnici vodorovnej čiary, príkladoch a často kladených otázkach týkajúcich sa vodorovných čiar a iných.
Obsah
- Definícia horizontálnej čiary
- Sklon vodorovnej čiary
- Kreslenie vodorovnej čiary
- Rovnica vodorovnej čiary
- Test horizontálnej čiary
- Vodorovné a zvislé čiary
- Rozdiely medzi vertikálnymi a horizontálnymi čiarami
- Krátka poznámka na vodorovnej čiare
- Príklady horizontálnych čiar
Definícia horizontálnej čiary
Vieme, že priamka je priama cesta, ktorá spája dva alebo viac dvoch bodov a vedie do nekonečna. Horizontálne čiary teda definujeme ako čiary, ktoré sú rovnobežné so zemou alebo horizontom a sú v konštantnej výške od zeme.
Ak nakreslíme tieto čiary na karteziánsky systém, potom tieto čiary sú čiary, ktoré nemajú priesečník na osi x, ale majú priesečník na osi y. Vodorovné čiary majú nulový sklon, t.j. majú nulový uhol s osou x alebo so zemou.
Horizontálne čiary tvoria základ rôznych objektov, tvarov a postáv, ktoré študujeme v geometrii. Predpokladajme, že musíme nakresliť obdĺžnik, štvorec, trojuholník, lichobežník , atď., potom základom týchto obrázkov sú väčšinou horizontálne čiary. Horizontálne lži pozorujeme aj v reálnom živote, pretože čiary na podlahe a streche miestností, základne schodiska atď. sú tiež vytvorené horizontálnymi čiarami.
Tieto línie sú tiež známe ako spiace línie, pretože nemajú žiadny vertikálny pohyb a vždy zostávajú v konštantnej výške od zeme. Obrázok pridaný nižšie zobrazuje vodorovnú čiaru.
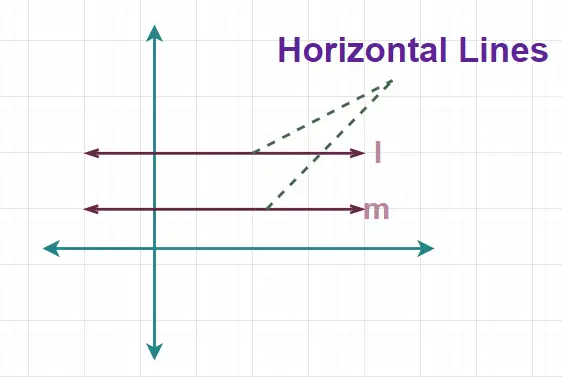
Tu na obrázku pridanom nad čiary l a m sú vodorovné čiary.
Sklon vodorovnej čiary
Už sme spomenuli, že sklon vodorovnej čiary je nulový . Teraz sa naučíme, ako je sklon vodorovnej čiary nulový. Sklon vodorovnej čiary vypočítame pomocou vzorca,
Sklon = stúpanie/beh
ALEBO
Sklon priamky = zmena y-ovej súradnice/zmena x-ovej súradnice
Kde Rise je výška získaná čiarou pri behu zľava doprava, keďže už vieme, že vodorovná čiara je rovnobežná s osou x a je vždy v konštantnej výške, teda hovoríme, že tieto čiary majú nulový vzostup, takže sklon týchto čiar je,
Teda sklon = 0/beh = 0
Dospelo sa teda k záveru, že sklon vodorovnej čiary je nulový.
Kreslenie vodorovnej čiary
Horizontálne čiary sa dajú ľahko nakresliť pomocou krokov uvedených nižšie,
Krok 1: Zoberme si bod na karteziánskej rovine, pre ktorý musíme nájsť vodorovnú čiaru. Predpokladajme, že bod je (1, 2)
Krok 2: Označuje y-ovú súradnicu bodu. V tomto prípade je súradnica y 2.
Krok 3: Označte ďalšie body, ktorých súradnica y je rovnaká ako bod v kroku 1. Ostatné body nech sú (-2, 2), (0, 2) a (7, 2)
Krok 4: Spojte všetky body, aby ste získali úsečku a predĺžte ich na obe strany, aby ste získali vodorovnú čiaru.
Toto je požadovaná vodorovná čiara prechádzajúca bodom (1, 2) a má sklon nula.

Rovnica vodorovnej čiary
Vieme, že rovnica priamky v 2-D súradnicovom systéme je,
y = mx + c
Kde,
nemenný zoznam
- m je sklon čiary
- c je priesečník na osi y
Vieme, že pre vodorovnú čiaru je sklon nulový. Nahradením tejto hodnoty vo vyššie uvedenej rovnici dostaneme rovnicu vodorovnej čiary,
y = 0x + c
y = c
Kde c je konštanta.
Vyššie uvedená rovnica y = c je teda rovnicou vodorovnej čiary.
Táto rovnica znamená, že vodorovná čiara je čiara, ktorá prechádza všetkými bodmi v karteziáne, kde sa súradnica y rovná „c“. Tento rez nemá súradnicu x, a preto táto čiara nikdy nepretína os x a prerezáva os y v bode (0, c).
Môžeme teda povedať, že rovnica vodorovnej priamky je y = c(konštantná) a prechádza bodom (a, c), kde a môže nadobudnúť ľubovoľnú hodnotu a c je vždy konštantné.
Test horizontálnej čiary
Test, ktorý sa používa na definovanie toho, či je funkcia funkciou jedna k jednej alebo nie, je test horizontálnej čiary. V teste vodorovnej čiary nakreslíme vodorovnú čiaru prechádzajúcu ktorýmkoľvek bodom funkcie a ak čiary prerušia funkciu v akomkoľvek inom bode, funkcia NIE JE funkciou jedna k jednej. Preto, aby bola funkcia jedna k jednej, musí prejsť testom vodorovnej čiary, t. j. každá vodorovná čiara musí funkciu prerušiť iba raz.
Vieme, že funkcie jedna ku jednej sú funkcie, kde pre každú hodnotu x máme iba jednu hodnotu y. Ak teda horizontálna čiara prechádza funkciou a pretína ju iba raz, môžeme povedať, že pre jedinečnú hodnotu y máme jedinečnú hodnotu x. Ak však horizontálna čiara pretína funkciu viac ako raz, dostaneme dve hodnoty pre jedinečnú hodnotu y, čo nie je prípad funkcie jedna ku jednej.
Test horizontálnej čiary nám pomáha určiť, či je funkcia funkciou One-One. To sa dá pochopiť pomocou obrázka pridaného nižšie.

Na prvom obrázku je funkcia jedna k jednej, pretože vodorovná čiara prechádza iba jedným bodom funkcie.
Na druhom obrázku funkcia NIE JE jedna k jednej, pretože horizontálna čiara prechádza cez viac ako jeden bod funkcie.
bash spánok
Vodorovné a zvislé čiary
Vodorovné čiary sú čiary, ktoré sú rovnobežné so zemou alebo horizontom. Tieto čiary sa tiež nazývajú spiace čiary. V karteziánskom systéme sú tieto čiary rovnobežné s osou x, zatiaľ čo pre zvislé čiary sú to čiary, ktoré sú kolmé na vodorovné čiary, nazývajú sa stojaté čiary. a sú rovnobežné s osou y v karteziánskom systéme.
Horizontálne čiary sú čiary, ktoré prebiehajú zľava doprava v karteziánskom systéme, zatiaľ čo vertikálne čiary sú čiary, ktoré prebiehajú nahor a nadol v karteziánskom systéme.
Zvislé a vodorovné čiary sú na seba kolmé. Obrázok pridaný nižšie zobrazuje zvislú a vodorovnú čiaru.

Rozdiely medzi vertikálnymi a horizontálnymi čiarami
Rozdiely medzi zvislými a vodorovnými čiarami možno ľahko pochopiť preštudovaním tabuľky pridanej nižšie.
| Horizontálna čiara | Vertikálna čiara |
|---|---|
| Tieto čiary sú rovnobežné so zemou alebo horizontom. | Tieto riadky sú kolmý k zemi alebo horizontu. |
| Sklon vodorovnej čiary je nulový. | Sklon zvislej čiary nie je definovaný. |
| Horizontálna čiara zvierala s horizontom uhol nula stupňov. | Vertikálna čiara zvierala s horizontom uhol 90 stupňov. |
| Rovnica vodorovnej čiary prechádzajúcej bodom (h, k) je, y = k | Rovnica zvislice prechádzajúcej bodom (h, k) je, x = h |
| Vodorovné čiary sú v karteziánskom systéme rovnobežné s osou x. | Vertikálne čiary sú v karteziánskom systéme rovnobežné s osou y. |
| Príklady reprezentujúce vodorovné čiary sú,
| Príklady predstavujúce zvislé čiary sú napr.
|
Krátka poznámka na vodorovnej čiare
Vodorovná čiara v matematike je dokonale rovná, rovnobežná s horizontom. Prebieha zľava doprava a má sklon 0. V geometrii je znázornená ako priamka spájajúca dva ľubovoľné body v rovnakej výške v rovine. Rovnica pre vodorovnú čiaru má tvar (y = k), kde (k) je konštantná hodnota predstavujúca výšku čiary na osi y.
Čítaj viac:
- Typy liniek
- Paralelné čiary
- Ako pridať vodorovnú čiaru do HTML?
- Ako použiť úplný horizontálny riadok v HTML?
- Ako nakresliť vodorovné a zvislé čiary v aplikácii pre Android pomocou XML
Príklady horizontálnych čiar
Príklad 1: Nájdite rovnicu vodorovnej priamky prechádzajúcej bodom (1, -1).
Riešenie:
Vieme, že sklon vodorovnej čiary je m = 0.
Daný bod (1, -1)
Rovnica priamky prechádzajúcej bodom (x1, a1) a so sklonom (m) je,
a – a1= m(x – x1)
Nahradením hodnôt vo vyššie uvedenej rovnici dostaneme,
y – (-1) = 0 (x – 1)
a + 1 = 0
y = -1
Rovnica vodorovnej priamky prechádzajúcej bodom (1, -1) je teda y = -1
Príklad 2: Nájdite rovnicu vodorovnej priamky prechádzajúcej bodom (5, 9).
Riešenie:
Vieme, že sklon vodorovnej čiary je m = 0.
vlc stiahnite si videá z youtubeDaný bod (5, 9)
Rovnica priamky prechádzajúcej bodom (x1, a1) a so sklonom (m) je,
a – a1= m(x – x1)
Nahradením hodnôt vo vyššie uvedenej rovnici dostaneme,
y – (9) = 0 (x – 5)
a – 9 = 0
y = 9
Rovnica vodorovnej priamky prechádzajúcej bodom (5, 9) je teda y = 9
Príklad 3: Nájdite rovnicu vodorovnej priamky, keď je priesečník priamky 5.
Riešenie:
Rovnica vodorovnej čiary je,
y = k
kde k je priesečník y
Dané
- k = 5
Rovnica vodorovnej čiary,
y = 5
Takže vodorovná čiara rovnice s priesečníkom y ako 5 je y = 5
Príklad 4: Nájdite rovnicu vodorovnej priamky, keď je priesečník v osi y -11/3.
Riešenie:
Rovnica vodorovnej čiary je,
y = k
kde k je priesečník y
Dané
kľúč na vloženie notebooku
- k = -11/3
Rovnica vodorovnej čiary,
y = -11/3
3r = -11
3 roky + 11 = 0
Takže vodorovná čiara rovnice s priesečníkom y ako -11/3 je 3y + 11 = 0
Horizontálne čiary – často kladené otázky
Čo sú vodorovné čiary?
Vodorovné čiary sú čiary, ktoré sú rovnobežné s horizontom alebo zemou. V karteziánskom systéme sú horizontálne čiary rovnobežné s osou x.
Aká je rovnica vodorovnej čiary?
Rovnica vodorovnej čiary je,
y = k
kde k je priesečník na osi y.
Aký je sklon vodorovnej čiary?
Sklon vodorovnej čiary je vždy rovný nule, pretože zvierajú s osou x uhol nula stupňov.
Aké sú príklady vodorovných čiar?
Príklady reprezentujúce vodorovné čiary sú,
- Rovná cesta
- Spodná časť schodiska
- Základňa ľubovoľnej figúry atď.
Ako sa nazývajú vodorovné čiary na zemeguli?
Vodorovné čiary prebiehajúce na zemeguli sa nazývajú zemepisné šírky a prebiehajú rovnobežne s rovníkom.
Aké sú vlastnosti vodorovných čiar?
Rôzne vlastnosti horizontálnych čiar sú,
- Sú rovnobežné so zemou, horizontom a osou x.
- Sú kolmé na os y.
- Sklon vodorovnej čiary je nulový atď.
Ktorá čiara je vertikálna a horizontálna?
Vertikálna čiara je rovnobežná s osou y a prebieha priamo nahor a nadol v súradnicovej rovine, zatiaľ čo vodorovná čiara je rovnobežná s osou x a prebieha priamo doľava a doprava.
Aký je sklon vodorovnej a zvislej čiary?
Sklon čiary označuje jej strmosť a smer. Vypočíta sa ako pomer vertikálnej zmeny k horizontálnej zmene medzi dvoma bodmi na priamke.
Aké sú horizontálne a vertikálne bodové čiary?
Vodorovné čiary sa rozprestierajú zľava doprava alebo sprava doľava a prebiehajú rovnobežne s osou x, zatiaľ čo zvislé čiary sa rozprestierajú nahor a nadol a prebiehajú rovnobežne s osou y. Tieto dva typy čiar sú na seba kolmé.
