Nuly polynómu sú tieto skutočné, imaginárne alebo komplexné hodnoty, keď sa do polynómu vložia namiesto premennej, výsledok sa stane nulou (ako aj názov napovedá nula). Polynómy sa používajú na modelovanie niektorých fyzikálnych javov odohrávajúcich sa v reálnom živote, sú veľmi užitočné pri matematickom opise situácií.

Nuly polynómu sú všetky hodnoty x, vďaka ktorým sa polynóm rovná nule. Nuly polynómu nám hovoria o priesečníkoch x v grafe polynómu. V tomto článku budeme diskutovať o nuly polynómu, ako ich nájsť, faktorová veta atď.

Obsah

• Čo sú nuly polynómov?
• Nuly polynomického vzorca
• Ako nájsť nulu polynómu?
• Pre lineárny polynóm
• Pre kvadratický polynóm
• Pre kubický polynóm
• Faktorová teoréma
• Vzťah medzi nulami a koeficientom
• Vzťah medzi nulami a koeficientom pre kvadratickú rovnicu
• Vzťah medzi nulami a koeficientom pre kubickú rovnicu
• Vytvorenie rovnice s nulami polynómu
• Nuly v grafe polynómov
• Základná veta lineárnej algebry
• Mnohonásobnosť koreňa
• Články súvisiace s nulami polynómu
• Ukážkové úlohy na nulách polynómu
• Cvičné úlohy na nulách polynómu

Čo sú nuly polynómov?

Pre polynóm P(x) hovoríme, že x = a je nula polynómu, ak P(a) = 0 a všetky takéto nuly polynómu sa bežne nazývajú nuly polynómu. Uvažujme napríklad f(x) = 3x – 12. Teraz do polynómu vložte x = 4, t.j. f(4) = 3×4 – 12 = 0. Teda x = 4 je nula polynómu f( x) = 3x – 12.

Príklad: Pre f(x) = x ³ – 6x ² + 11x – 6, je x = 1 nula?

Riešenie:

Skontrolujte, či ak x = 1 je nula z f(x) = x³– 6x²+ 11x – 6 alebo nie, vložte x = 1 do (x)

f(1) = (1)³– 6×(1)²+ 11×(1) – 6

⇒ f(1) = 1 – 6 + 11 – 6 = 12 -12 = 0

Teda x = 1 je nula z f(x).

Nuly polynomického vzorca

Pre lineárny polynóm tvaru ax + b je jeho nula daná x = -b/a.

d žabka

Pre kvadratický polynóm tvaru ax²+ bx + c, jeho nula je daná x = {- b ± √D}/2a, kde D je diskriminačné dané b²– 4ac.

Ako nájsť nulu polynómu?

Nuly polynómu môžeme nájsť pre rôzne typy polynómov pomocou rôznych metód, ktoré sú popísané nižšie.

• Pre lineárny polynóm
• Pre kvadratický polynóm
• Pre kubický polynóm

Pre lineárny polynóm

Pre lineárne polynómy je nájdenie nuly najjednoduchšie zo všetkých. pretože je len jedna nula a tá sa dá vypočítať aj jednoduchým preskupením polynómu za zrovnovacím polynómom na 0.

Napríklad nájdite nulu pre lineárny polynóm f(x) = 2x – 7.

Riešenie:

Ak chcete nájsť nulu z f(x), prirovnajte f(x) k 0.

⇒ 2x – 7 = 0

⇒ 2x = 7

⇒ x = 7/2

Pre kvadratický polynóm

Existujú rôzne metódy na nájdenie koreňov alebo núl kvadratického polynómu, ako je rozdelenie stredného člena, kvadratický vzorec, ktorý je známy aj ako vzorec Shree Dharacharya, a dokončenie štvorca, ktorý je trochu podobný kvadratickému vzorcu, ako prichádza kvadratický vzorec. od doplnenia štvorca pre všeobecnú kvadratickú rovnicu.

Naučiť sa viac o riešenie kvadratických rovníc alebo polynómy a ako ich riešiť. Nasledujúce príklady podrobne ukazujú metódu hľadania núl kvadratických polynómov.

Príklad 1: Zistite nuly pre P(x) = x ² + 2x – 15.

odpoveď:

X²+ 2x – 15 = 0

⇒ x²+ 5x – 3x – 15 = 0

⇒ x(x + 5) – 3(x + 5) = 0

⇒ (x – 3) (x + 5) = 0

⇒ x = 3, -5

Príklad 2: Nájdite nuly pre P(x) = x ² – 16x + 64.

odpoveď:

X²– 16x + 64 = 0

Porovnanie so sekerou²+ bx + c = 0,

dostaneme, a = 1, b = -16 a c = 64.

teda

⇒ x = 8, 8

Pre kubický polynóm

Na nájdenie kubických núl existuje mnoho spôsobov, ako napríklad racionálna koreňová veta a dlhé delenie. Jedna metóda hľadania koreňov kubického alebo akéhokoľvek polynómu vyššieho stupňa je nasledovná:

Krok 1: Na nájdenie možných koreňov použite racionálnu koreňovú vetu. t.j. Ak má polynóm racionálny koreň, musí to byť delenie p/q, kde p je celočíselná konštanta a q je vedúci koeficient.

Krok 2: Po nájdení jedného koreňa rozdeľte polynóm s faktorom tvoreným týmto koreňom pomocou dlhého delenia a napíšte polynóm ako súčin podielu a dividendy.

Krok 3: Ak je kvocient kvadratický výraz, vyriešte ho metódami uvedenými vyššie pre kvadratické polynómy. Ak nejde o polynóm 2. stupňa, opakujte kroky 1 a 2, kým sa z kvocientu nestane polynóm 2. stupňa.

Krok 4: Výsledkom kroku 3 sú požadované faktory a prirovnaním faktora k 0 môžeme nájsť nuly polynómu.

Príklad: Nájdite nuly kubického polynómu p(x) = x ³ + 2x ² – 5x – 6.

Riešenie:

p(x) = x³+ 2x²– 5x – 6

Ako p/q = -6

Podľa racionálnej koreňovej vety sú všetky možné racionálne korene polunomiku deliteľmi p/q.

Deliče = ±1, ±2, ±3, ±6

x = -1, v p(x), dostaneme

p(-1) = (-1)³+ 2 (-1)²– 5 (-1) – 6

⇒ p(-1) = -1 + 2 + 5 – 6 = 0

Podľa faktorovej vety je teda x + 1 faktor p(x).

Teda x³+ 2x²– 5x – 6 = (x+1) (x²+x – 6)

⇒ x³+ 2x²– 5x – 6 = (x+1)(x-2)(x+3)

Pre nuly je p(x) = 0,

Nuly p(x) sú x = -1, x = 2 a x = -3.

Faktorová teoréma

Pre polynóm P(x) faktorová veta hovorí, že ak x =a je nula P(X), ak x – a je faktor P(x). t.j. mali by platiť obe nasledujúce podmienky.

• Ak a je nula P(x), potom x−a bude faktor P(x)
• Ak x−a je faktor P(x), potom a bude nula P(x)

Dá sa to overiť pohľadom na predchádzajúce príklady. Faktorová veta môže viesť k zaujímavým výsledkom, ktoré sú nasledovné:

Výsledok 1: Ak P(x) je polynóm stupňa n a r je nula P(x), potom P(x) možno zapísať v nasledujúcom tvare:

P(x) = (x – r) Q(x)

Kde Q(x) je polynóm stupňa n-1 a dá sa zistiť delením P(x) s (x – r).

Výsledok 2: Ak P(x) = (x-r)Q(x) a x = t je nula z Q(x), potom x = t bude tiež nula z P(x).

Na overenie vyššie uvedenej skutočnosti,

Povedzme, že t je nula Q(x), čo znamená Q(t) = 0.

Vieme, že r je nula polynómu P(x), kde P(x) = (x – r) Q(x),

Takže musíme skontrolovať, či x = t je tiež nula P(x), dajme x = t do P(x)

⇒ P(t) = (t – r) Q(t) = 0

Takže x = t je tiež nula P(x).

Preto Dokázané.

Vzťah medzi nulami a koeficientom

Vzťah medzi nulami a koeficientom kvadratickej a kubickej rovnice je diskutovaný nižšie.

Vzťah medzi nulami a koeficientom pre kvadratickú rovnicu

Pre kvadratickú rovnicu tvaru ax²+ bx + c = 0, ak sú dve nuly kvadratickej rovnice α a β, potom

• Súčet odmocniny = α + β = -b/a
• Súčin koreňov = α × β = c/a

Vzťah medzi nulami a koeficientom pre kubickú rovnicu

Ak sú α, β a γ koreňom kubickej osi polynómu³+ bx²+ cx + d = 0, potom vzťah medzi jeho nulami a koeficientmi je daný takto:

• a + b + c = -b/a
• a x β x y= -d/a
• αβ + αγ + βγ = c/a

Vytvorenie rovnice s nulami polynómu

• Pre kvadratický polynóm s nulami α a β je kvadratický polynóm daný vzťahom

X ² – (a + b)x + ab .

• Pre kubický polynóm s tromi nulami α, β a γ je kubický polynóm daný vzťahom

X ³ – (a + b + c )x ² + (ab + ag + bg)x – abg

Nuly v grafe polynómov

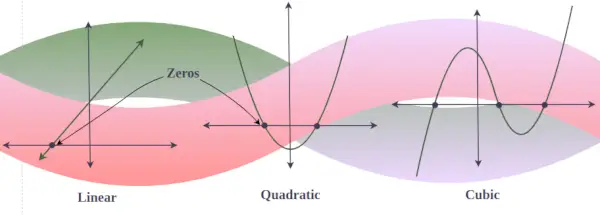
V grafe ľubovoľného polynómu y = f(x) sú reálne nuly bod, pre ktorý graf pretína alebo sa dotýka osi x. (keďže graf s imaginárnou nulou nikdy nepretína os x). Inými slovami, ak existujú 3 reálne riešenia kubického polynómu, potom graf tohto kubického polynómu pretína os x trikrát, ale ak pre nejaký kubický polynóm existuje len jedno reálne riešenie, potom graf pretína iba os x. raz.

Základná veta lineárnej algebry

Ak P(x) je polynóm stupňa n, potom P(x) bude mať presne n núl, z ktorých niektoré sa môžu opakovať.

To znamená, že ak vypíšeme všetky nuly a každú uvedieme k-krát, keď k je jej násobnosť. V zozname budeme mať presne n čísel. To môže byť užitočné, pretože nám to môže poskytnúť predstavu o tom, koľko núl by malo byť v polynóme. Takže môžeme prestať hľadať nuly, keď dosiahneme požadovaný počet núl.

Mnohonásobnosť koreňa

Predpokladajme, že máme polynóm P(x) = 0, ktorý sa rozkladá na,

P(x) = (x – r) ^k (x – a) ^m

Ak r je nula polynómu a exponent na jeho člene, ktorý vytvoril koreň, je k, potom hovoríme, že r má mnohosť k . Často sa nazývajú nuly s násobnosťou 1 jednoduché nuly a nuly s násobnosťou 2 sa nazývajú dvojité korene polynómu.

Príklad: P(x) je polynóm 5. stupňa, ktorý bol pre vás faktorizovaný. Uveďte korene a ich početnosť.

P(x) = 5x ⁵ -20x ⁴ +5x ³ +50x ² −20x−40=5(x+1) ² (x-2) ³

Riešenie:

Dané, P(x) = 5 (x+1)²(x-2)³

⇒ P(x) = 5(x+1)(x+1)(x+1)(x−2)(x−2)

Ak chcete nájsť nuly, P(x) = 0

⇒ x = -1, -1, 2, 2, 2

Všimnite si, že -1 sa vyskytuje dvakrát ako nula, takže jej násobnosť je 2, zatiaľ čo násobnosť nuly 2 je 3.

Články súvisiace s nulami polynómu

• Polynóm
• Korene kvadratickej rovnice
• Algebraický výraz

Ukážkové úlohy na nulách polynómu

Úloha 1: Vzhľadom na to, že x = 2 je nula z P(x) = x ³ +2x ² −5x−6. Nájdite ďalšie dve nuly.

Riešenie:

Zo základnej vety, ktorú sme študovali skôr, môžeme povedať, že P(x) bude mať 3 nuly, pretože ide o trojstupňový polynóm. Jeden z nich je x = 2.

Takže môžeme prepísať P(x),

P(x) = (x – 2) Q(x)

Na nájdenie ďalších dvoch núl potrebujeme zistiť Q(x).

Q(x) možno zistiť vydelením P(x) číslom (x-2).

Po rozdelení vyjde Q(x) takto:

Q(x) = x²+ 4x + 3

Z toho sa dajú zistiť zvyšné dve nuly,

Q(x) = x²+ 3x + x + 3

⇒ x(x + 3) + 1 (x + 3)

⇒ (x + 1) (x + 3)

Q(x) = 0,

x = -1, -3

Ďalšie dve nuly sú teda x = -1 a x = -3.

Úloha 2: Vzhľadom na to, že x = r je nula polynómu, zistite ostatné nuly polynómu.

P(x) = x ³ -6x ² −16x; r = -2

Riešenie:

Vieme, že x = -2 je nula,

Takže P(x) možno prepísať ako, P(x) = (x + 2) Q(x) {pomocou deliaceho algoritmu}

Teraz, aby sme našli Q(x), urobíme to isté, čo sme urobili v predchádzajúcej otázke, rozdelíme P(x) s (x + 2).

Dostaneme,

Q(x) = x²– 8x

Teraz, aby ste našli ďalšie dve nuly, faktorizujte Q(x)

Q(x) = x (x – 8) = 0

Takže nuly sú x = 0, 8.

Máme teda tri nuly, x = -2, 0, 8.

Úloha 3: Nájdite nuly polynómu, 4x ³ -3x ² -25x-6 = 0

Riešenie:

Trik na riešenie polynomických rovníc so stupňom 3,

Nájdite najmenšie celé číslo, ktoré môže vytvoriť polynóm 0, začnite s 1,-1,2 atď.

zistíme, že pre x = -2 dostaneme hodnotu výrazu nulovú.

Jeden z koreňov je teda -2.

Podľa vety o faktore, ak a je jedna z núl polynómu, teda (x-a) je faktor daného polynómu.

Za týmto {x – (-2)} = (x+2) je teda faktor pof nad polynómom.

Dostaneme kvadratickú rovnicu a už tam sú nuly.

(4x²-11x-3)(x+2) = 0

Faktorizujte kvadratickú rovnicu,

(4x²-12x+x-3)(x+2) = 0

[4x(x-3)+1(x-3)](x+2) = 0

(4x+1)(x-3)(x+2) = 0

x = -2, x = 3, x = -1/4

Úloha 4: Nájdite nuly polynómu, 4x ⁶ – 16x ⁴ = 0

Riešenie:

Polynóm má až 6. stupeň, preto existuje 6 núl polynómu.

4x⁴(X²-4) = 0

4x⁴(X²-2²) = 0

4x⁴[(x+2)(x-2)] = 0

Preto x = 0, 0, 0, 0, 2, -2

Úloha 5: Nájdite nuly polynómovej funkcie f(x) = x ³ – 2x ² - 5x + 6

Riešenie:

Aby sme našli nuly tohto polynómu, nastavíme f(x) = 0 a vyriešime x:

f(x) = x³– 2x²– 5x + 6 = 0

Ako d/a = 6

Podľa racionálnej koreňovej vety sú všetky možné racionálne korene polunomie

Deliče d/a = ±1, ±2, ±3, ±6

x = 1, v p(x) dostaneme

f(1) = (1)³– 2(1)²– 5(1) – 6

f(-1) = 1 – 2 – 5 + 6 = 0

Podľa faktorovej vety je teda x – 1 faktorom p(x).

Teda x³+ 2x²– 5x – 6 = (x-1) (x²-x – 6)

X³+ 2x²– 5x – 6 = (x-1)(x+2)(x-3)

Pre nuly je p(x) = 0,

Nuly p(x) sú x = 1, x = -2 a x = 3.

Cvičné úlohy na nulách polynómu

1. Nájdite všetky nuly polynómu f(x) = x ³ – 6x ² + 11x – 6

2. Určte všetky nuly polynómu g(x) = 2x ⁴ – 7x ³ + 3x ² + 4x – 4

3. Nájdite nuly polynómu h(x) = x ⁵ – 3x ⁴ + 2x ³ – 6x ² + x + 2

4. Určte všetky nuly polynómu p(x) = 3x ⁴ – 16x ³ + 18x ² + 16x – 12.

Časté otázky o nulách polynómu

Čo sú nuly polynómu?

Tieto reálne hodnoty sa pre hodnotu polynómu stanú 0, t.j. ak p(x) je polynóm a p(a) = 0, potom x = a je nula z p(x).

Ako nájsť nuly polynómu?

Existujú rôzne metódy pre rôzne polynómy na nájdenie núl, ako napríklad pre kvadratické rozloženie stredného člena a kvadratický vzorec. Pre lineárne, jednoduché preskupenie premenných a pre kubické používame kombináciu racionálnej koreňovej vety, dlhého delenia, faktorovej vety a zostatkovej vety.

Môže mať polynóm viac ako jednu nulu?

Áno, polynóm môže mať viac ako jednu nulu, v skutočnosti polynóm n stupňov môže mať najviac n skutočných núl.

Aká je násobnosť nuly polynómu?

V procese faktorizácie, jeden faktor alebo jedna nula polynómu, potom niekoľkokrát prišiel faktor alebo nula, čo sa nazýva multiplicita tohto koreňa.

nastaviť v jave

Čo je základná veta algebry?

Základná veta stavov algebry Ak P(x) je polynóm stupňa n, potom P(x) bude mať presne n núl, z ktorých niektoré sa môžu opakovať.

Má polynóm so stupňom n vždy n skutočných koreňov?

Nie, polynóm so stupňom n nemá vždy n skutočných koreňov, pretože niektoré korene môžu byť imaginárne alebo komplexné čísla.

Aký je stupeň nulového polynómu?

Stupeň nulového polynómu je nula.