Trenie je sila, ktorá odoláva relatívnemu pohybu a vyskytuje sa na rozhraní medzi telesami, ale aj vo vnútri telies, ako v prípade tekutín. Koncept koeficientu trenia prvýkrát sformuloval Leonardo da Vinci. Veľkosť koeficientu trenia je určená vlastnosťami povrchov, okolia, povrchových vlastností, prítomnosti maziva atď.
Zákony trenia
Existuje päť zákonov trenia a sú:
• Trenie pohybujúceho sa objektu je úmerné a kolmé na normálovú silu.
• Trenie, ktorému objekt čelí, závisí od povahy povrchu, s ktorým je v kontakte.
• Trenie je nezávislé od oblasti kontaktu, pokiaľ existuje oblasť kontaktu.
• Kinetické trenie je nezávislé od rýchlosti.
• Koeficient statického trenia je väčší ako koeficient kinetického trenia.
Keď vidíme akýkoľvek objekt, môžeme vidieť hladký povrch, ale keď sa na ten istý objekt pozrieme pod mikroskopom, môžeme vidieť, že aj hladko vyzerajúci objekt má drsné hrany. Mikroskopom je možné vidieť drobné kopčeky a ryhy, ktoré sú známe ako nepravidelnosti povrchu. Takže, keď sa jeden predmet pohybuje cez druhý, tieto nepravidelnosti na povrchu sa zapletú, čo vedie k treniu. Čím je drsnosť, tým viac nerovností a väčšia sila.
Statické trenie
Existuje niekoľko teórií týkajúcich sa príčin statického trenia a ako väčšina konceptov súvisiacich s trením, každá z nich sa za určitých podmienok ukáže ako platná, ale za iných okolností zlyhá. Pre aplikácie v reálnom svete (najmä tie, ktoré sa týkajú priemyselných strojov a pohybu). Ovládajte dve najrozšírenejšie teórie stojace za statickým trením, ktoré súvisia s mikroskopickou drsnosťou povrchov.
Bez ohľadu na to, ako dokonale je povrch opracovaný, dokončený a vyčistený, bude mať nevyhnutne nerovnosti – v podstate drsnosť pozostávajúcu z vrcholov a údolí, podobne ako pohorie. (Technicky vrcholy sú nerovnosti.) Keď sú dva povrchy v kontakte, môže sa zdať, že majú veľkú, dobre definovanú oblasť kontaktu, ale v skutočnosti dochádza ku kontaktu iba na určitých miestach – teda tam, kde sú nerovnosti oba povrchy prekážajú.
Súčet týchto malých oblastí kontaktu medzi asperitami sa označuje ako skutočná alebo efektívna oblasť kontaktu. Pretože tieto jednotlivé oblasti kontaktu sú veľmi malé, tlak (tlak = sila ÷ plocha) medzi povrchmi v týchto bodoch je veľmi vysoký. Tento extrémny tlak umožňuje, aby došlo k adhézii medzi povrchmi prostredníctvom procesu známeho ako zváranie za studena, ku ktorému dochádza na molekulárnej úrovni. Predtým, ako sa povrchy môžu navzájom pohybovať, musia byť prerušené väzby, ktoré spôsobujú túto adhéziu.
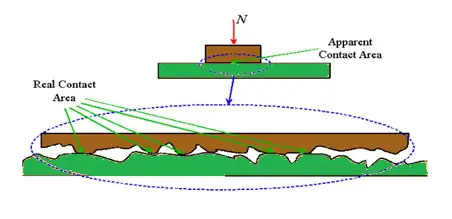
Okrem toho drsnosť povrchov znamená, že na niektorých miestach sa nerovnosti jedného povrchu usadia do úžľabia druhého povrchu – inými slovami, povrchy sa do seba zapadnú.
Tieto do seba zapadajúce oblasti musia byť rozbité alebo plasticky deformované predtým, ako sa môžu povrchy pohybovať. Inými slovami, musí dôjsť k oderu. Takže vo väčšine aplikácií je statické trenie spôsobené priľnavosťou aj odieraním kontaktných povrchov.
Zákony statického trenia
Existujú dva zákony statického trenia:
- Prvý zákon: Maximálna sila statického trenia nezávisí od oblasti kontaktu.
- Druhý zákon: Maximálna sila statického trenia je porovnateľná s normálnou silou, t.j. ak sa normálová sila zvýši, zvýši sa aj maximálna vonkajšia sila, ktorú môže objekt vydržať bez pohybu.

Odvodenie pre vzorec statického trenia
Uvažujme blok hmotnosti mg ležiaci na vodorovnom povrchu, ako je znázornené na obrázku. Keď telo tlačí na povrch, povrch sa deformuje, aj keď sa zdá byť tuhý. Deformovaný povrch tlačí teleso normálovou silou R, ktorá je kolmá na povrch. Toto sa nazýva normálna reakčná sila. Vyvažuje to mg
R = mg
Teraz uvažujme, že na blok pôsobí sila P. Je zrejmé, že teleso zostáva v pokoji, pretože v horizontálnom smere vstupuje do hry iná sila F a pôsobí proti aplikovanej sile P, čo vedie k nulovej sile na tele. Táto sila F pôsobiaca pozdĺž povrchu telesa v kontakte s povrchom stola sa nazýva trecia sila.
Takže pokiaľ sa teleso nehýbe, F = P. To znamená, že ak zvýšime P, zvýši sa aj trenie F, pričom vždy zostane rovné P.
Táto trecia sila, ktorá vstupuje do hry, kým sa nezačne skutočný pohyb, je známa ako statické trenie.
Koeficient statického trenia
Statické trenie je trenie, ku ktorému dochádza, keď je predmet umiestnený na povrchu. A kinetické trenie je spôsobené pohybom objektu na povrchu. Trenie je dobre charakterizované koeficientom trenia a vysvetľuje sa ako pomer medzi trecou silou a normálnou silou. To pomáha objektu ležať na povrchu. Koeficient statického trenia je skalárna veličina a označuje sa ako μs.
Vzorec pre koeficient statického trenia je vyjadrený ako
mu_{s} = frac{F}{N} Kde
m s = koeficient statického trenia
F = statická trecia sila
N = normálna sila

Kinetické trenie
Kinetické trenie je definované ako sila, ktorá pôsobí medzi pohyblivými povrchmi. Na teleso pohybujúce sa na povrchu pôsobí sila v opačnom smere svojho pohybu. Veľkosť sily bude závisieť od koeficientu kinetického trenia medzi týmito dvoma materiálmi.
Trenie je ľahko definované ako sila, ktorá zadržiava posúvajúci sa predmet. Kinetické trenie je súčasťou všetkého a ruší pohyb dvoch alebo viacerých predmetov. Sila pôsobí v opačnom smere, ako sa chce predmet posúvať.
Ak auto musí zastaviť, zabrzdíme a to je presne to miesto, kde sa prejaví trenie. Pri chôdzi, keď sa chce človek náhle zastaviť, trenie znamená opäť poďakovať. Ale keď musíme zastaviť uprostred kaluže, veci sa stávajú ťažšie, pretože trenie je menšie a nemôže nám tak pomôcť.

Prekonanie statického trenia medzi dvoma povrchmi v podstate odstraňuje molekulárne prekážky (studené zváranie medzi drsnosťami) a do určitej miery aj mechanické prekážky (interferencie medzi drsnosťami a úžľabiami povrchov) pohybu. Akonáhle je pohyb iniciovaný, dochádza k určitému odieraniu, ale na oveľa nižšej úrovni ako počas statického trenia a relatívna rýchlosť medzi povrchmi poskytuje nedostatočný čas na uskutočnenie dodatočného studeného zvárania (okrem prípadu extrémne nízkej rýchlosti).
Keď je väčšina adhézie a oderu prekonaná na vyvolanie pohybu, odpor voči pohybu medzi povrchmi sa zníži a povrchy sa teraz pohybujú pod vplyvom kinetického trenia, ktoré je oveľa nižšie ako statické trenie.
Zákony kinetického trenia
Existujú štyri zákony kinetického trenia:
- Prvý zákon: Sila kinetického trenia (Fk) je priamo úmerná normálnej reakcii (N) medzi dvoma povrchmi, ktoré sú v kontakte. Kde, m k = konštanta nazývaná koeficient kinetického trenia.
- Druhý zákon: Sila kinetického trenia je nezávislá od tvaru a zdanlivej plochy povrchov, ktoré sú v kontakte.
- Tretí zákon: Závisí to od povahy a materiálu povrchu, ktorý je v kontakte.
- Štvrtý zákon: Je nezávislá od rýchlosti objektu v kontakte za predpokladu, že relatívna rýchlosť medzi objektom a povrchom nie je príliš veľká.

Vzorec kinetického trenia
Koeficient kinetického trenia sa označuje gréckym písmenom mu ( m ), s dolným indexom k. Sila kinetického trenia je m k násobok normálovej sily pôsobiacej na teleso. Vyjadruje sa v Newtonoch (N).
Rovnicu kinetického trenia možno zapísať takto:
Sila kinetického trenia = (koeficient kinetického trenia) (normálna sila)
F k = m k h
Kde,
F k = sila kinetického trenia
m k koeficient kinetického trenia
h = normálna sila (grécke písmeno eta)

Odvodenie pre vzorec kinetického trenia
Zoberme si blok hmotnosti mg ležiace na vodorovnom povrchu, ako je znázornené na obrázku. Keď telo tlačí na povrch, povrch sa deformuje, aj keď sa zdá byť tuhý. Deformovaný povrch tlačí teleso normálovou silou R ktorá je kolmá na povrch. Toto sa nazýva normálna reakčná sila. Vyvažuje to mg R = mg .
python uložte json do súboru
Teraz to považujme za silu P sa aplikuje na blok, ako je znázornené. Je zrejmé, že telo zostáva v pokoji kvôli nejakej inej sile F vstupuje do hry v horizontálnom smere a pôsobí proti pôsobiacej sile P výsledkom je nulová sila na tele. Táto sila F pôsobiaca po povrchu telesa v kontakte s povrchom stola sa nazýva trecia sila .
Takže pokiaľ sa telo nehýbe F = P . To znamená, že ak zväčšíme P, zvýši sa aj trenie F, pričom zostane vždy rovné P.
Keď aplikovanú silu mierne zvýšime nad limitné trenie, začne sa skutočný pohyb. To neznamená, že trenie zmizlo. Znamená to len, že sila prekonala obmedzujúce trenie. Táto sila trenia v tomto štádiu je známa ako kinetické trenie alebo dynamické trenie.
Kinetické trenie alebo dynamické trenie je protichodná sila, ktorá vstupuje do hry, keď sa telo skutočne pohybuje po povrchu iného telesa.
Aplikácia statického a kinetického trenia

Aplikácie statického trenia
Niektoré reálne príklady statického trenia sú uvedené v nasledujúcich bodoch:
- Papiere na doske stola
- Uterák visiaci na stojane
- Záložka v knihe
- Auto zaparkované na kopci
Aplikácie kinetického trenia
Niektoré reálne príklady kinetického trenia sú uvedené v bodoch nižšie.
- Trenie tiež zohráva obrovskú úlohu pri každodenných udalostiach, ako je trenie dvoch predmetov. Výsledný pohyb sa premieňa na teplo, čo v niektorých prípadoch vedie k požiaru.
- Je tiež zodpovedný za opotrebovanie, a preto potrebujeme olej na mazanie častí strojov, pretože znižuje trenie.
- Pri trení dvoch predmetov o seba sa trecia sila premení na tepelnú energiu, ktorá v niekoľkých prípadoch vedie k požiaru
- Kinetické trenie je zodpovedné za opotrebovanie častí stroja, preto je dôležité časti stroja mazať olejom.
Rozdiel medzi statickým a kinetickým trením
| Statické trenie | Kinetické trenie |
| Statické trenie je trenie medzi dvoma alebo viacerými predmetmi, ktoré sa navzájom nepohybujú | Kinetické trenie je trenie medzi dvoma alebo viacerými objektmi, ktoré sú voči sebe v pohybe. |
| Veľkosť statického trenia je väčšia vďaka väčšej hodnote jeho koeficientu. | Veľkosť kinetického trenia je porovnateľne menšia v dôsledku nízkej hodnoty jeho koeficientu. |
Rovnica predstavujúca statické trenie je daná Fs= msh | Rovnica predstavujúca kinetické trenie je daná vzťahom Fk= mkh |
| Jeho hodnota môže byť nula. | Jeho hodnota nikdy nemôže byť nulová. |
| Príklad- Ceruzka na stole. | Príklad – Presunutie ceruzky cez dosku stola. |
Vzorové problémy založené na statickom a kinetickom trení
Otázka 1: Muž tlačí cez podlahu veľkú lepenku s hmotnosťou 75,0 kg.
Riešenie:
Koeficient kinetického trenia je μk= 0,520
Pracovník pôsobí silou 400,0 N dopredu.
Aká je veľkosť sily trenia?
Odpoveď: Na rovnom povrchu možno pomocou vzorca zistiť normálovú silu objektu
h = mg
Dosadením hodnoty η do rovnice Fk= mkη, dostávame
Fk= (0,520) (75,0 kg) (9,80 m/s2) = 382,2 N
Otázka 2: Vo vyššie uvedenej otázke vypočítajte čistú silu pohybu krabice?
Riešenie:
Čistá sila pôsobiaca na teleso je súčtom všetkých síl pôsobiacich na teleso.
V tomto prípade sú sily pôsobiace na teleso sila vyvíjaná človekom a kinetické trenie pôsobiace v opačnom smere.
Ak sa pohyb dopredu považuje za kladný, potom sa čistá sila vypočíta takto:
Fnet= Fpracovník– Fk
Dosadením hodnôt vo vyššie uvedenej rovnici dostaneme
Fnet= 400 N – 382,2 N = 17,8 N
Otázka 3: Prečo pri valivom pohybe dochádza k treniu?
odpoveď:
Teoreticky má loptička bodový kontakt s povrchom.
V skutočnosti sa však loptička (a/alebo povrch) vplyvom zaťaženia deformuje a kontaktná plocha sa stáva eliptickou.
Teoreticky by valivé povrchy, aké sa nachádzajú vo väčšine rotačných a lineárnych ložísk (okrem klzných ložísk), nemali naraziť na trecie sily.
Ale v reálnych aplikáciách spôsobujú trenie vo valivých povrchoch tri faktory:
1. Mikrosklz medzi povrchmi (povrchy sa navzájom posúvajú)
2. Neelastické vlastnosti (t.j. deformácia) materiálov
3. Drsnosť povrchov
Otázka 4: Predmet s hmotnosťou 10 kg je umiestnený na hladkom povrchu. Statické trenie medzi týmito dvoma povrchmi je dané ako 15 N. Nájdite koeficient statického trenia?
Riešenie:
Dané
m = 10 kg
F = 15 N
ms= ?
My to vieme,
Normálna sila, N = mg
Takže, N = 10 × 9,81 = 98,1 N
Vzorec pre koeficient statického trenia je:
ms= 15/N
bfs a dfsms= 15/98,1
m s = 0,153
Otázka 5: Normálna sila a statická trecia sila objektu sú 50 N a 80 N. Nájdite koeficient statického trenia?
Riešenie:
Dané
N = 50 N
F = 80 N a μs= ?
Vzorec pre koeficient statického trenia je
ms= F/N
ms= 80/50
ms= 1,6
Otázka 6: Aký je vzťah medzi statickým a kinetickým trením?
odpoveď:
Sila statického trenia udržuje nehybný objekt v pokoji. Akonáhle je sila statického trenia prekonaná, sila kinetického trenia je to, čo spomalí pohybujúci sa objekt.
Otázka 7: Chladnička váži 1619 N a koeficient statického trenia je 0,50. Aká najmenšia sila sa používa na pohyb chladničky?
Riešenie:
Uvedené údaje:
Hmotnosť chladničky, W=1619 N
W = 1619 N
Koeficient statického trenia, μs= 0,50
Minimálna sila potrebná na pohyb chladničky môže byť daná ako,
F = msIN
F = 0,50 x 1619
F = 809,50 N.
