Rekurzívnu funkciu možno definovať ako rutinu, ktorá sa volá priamo alebo nepriamo.
Inými slovami, rekurzívna funkcia je funkcia, ktorá rieši problém riešením menších prípadov toho istého problému. Táto technika sa bežne používa v programovaní na riešenie problémov, ktoré možno rozdeliť na jednoduchšie, podobné podproblémy.
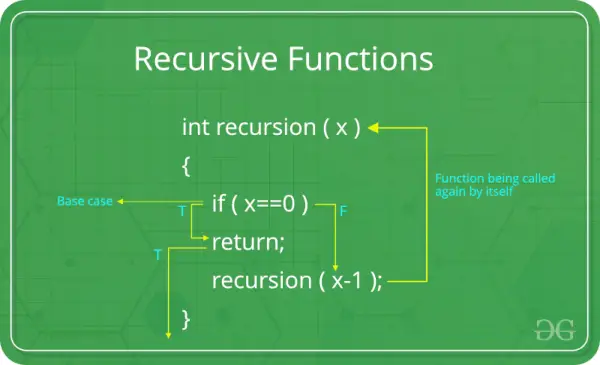
Potreba rekurzívnej funkcie:
Rekurzívna funkcia je funkcia, ktorá rieši problém riešením menších prípadov toho istého problému. Táto technika sa často používa v programovaní na riešenie problémov, ktoré možno rozdeliť na jednoduchšie, podobné podproblémy.
nahradiť reťazec v jazyku Java
1. Riešenie zložitých úloh:
Rekurzívne funkcie rozkladajú zložité problémy na menšie prípady toho istého problému, čo vedie ku kompaktnému a čitateľnému kódu.
2. Rozdeľ a panuj:
Rekurzívne funkcie sú vhodné pre algoritmy rozdeľuj a panuj, ako napríklad zlúčenie triedenia a rýchleho triedenia, rozdelenie problémov na menšie podproblémy, ich rekurzívne riešenie a zlúčenie riešení s pôvodným problémom.
3. Backtracking :
Rekurzívne spätné sledovanie je ideálne na skúmanie a riešenie problémov ako N-Queens a Sudoku.
4. Dynamický programovanie:
Rekurzívne funkcie efektívne riešia problémy dynamického programovania riešením čiastkových problémov a kombinovaním ich riešení do kompletného riešenia.
5. Strom a štruktúry grafov:
Rekurzívne funkcie sú skvelé na prácu so stromovými a grafovými štruktúrami, zjednodušujú úlohy prechodu a rozpoznávania vzorov .
Ako napísať rekurzívnu funkciu:
Komponenty rekurzívnej funkcie:
Základný prípad: Každá rekurzívna funkcia musí mať základný prípad. Základný prípad je najjednoduchší scenár, ktorý nevyžaduje ďalšiu rekurziu. Toto je podmienka ukončenia, ktorá bráni funkcii volať samu seba donekonečna. Bez správneho základného prípadu môže rekurzívna funkcia viesť k nekonečnej rekurzii.
rozdiel dátumov v exceli
Rekurzívny prípad: V rekurzívnom prípade funkcia volá sama seba s upravenými argumentmi. Toto je podstata rekurzie – riešenie väčšieho problému jeho rozdelením na menšie prípady toho istého problému. Rekurzívny prípad by sa mal pri každej iterácii približovať k základnému prípadu.
Uvažujme o príklade faktoriál čísla :
V tomto príklade je základný prípad kedy n je 0 a funkcia sa vráti 1 . Rekurzívny prípad sa znásobuje n s výsledkom funkcie volanej s parametrom n – 1 . Proces pokračuje, kým sa nedosiahne základný prípad.
Je dôležité zabezpečiť, aby rekurzívna funkcia mala správny základný prípad a aby rekurzívne volania viedli k základnému prípadu, inak môže procedúra bežať donekonečna, čo vedie k pretečeniu zásobníka (prekročenie dostupnej pamäte pridelenej pre volania funkcií).
Nižšie je implementácia faktoriálu čísla:
C++ #include using namespace std; // Recursive Function to calculate Factorial of a number int factorial(int n) { // Base case if (n == 0) { return 1; } // Recursive case return n * factorial(n - 1); } // Driver Code int main() { int n = 4; cout << 'Factorial of ' << n << ' is:' << factorial(n); return 0; }> Java import java.util.Scanner; public class Factorial { // Recursive Function to calculate the factorial of a number static int factorial(int n) { // Base case: If n is 0, the factorial is 1. if (n == 0) { return 1; } // Recursive case: Calculate the factorial by multiplying n with the factorial of (n - 1). return n * factorial(n - 1); } public static void main(String[] args) { int n = 4; // Calculate and print the factorial of n. int result = factorial(n); System.out.println('Factorial of ' + n + ' is: ' + result); } }> Python # Recursive Function to calculate Factorial of a number def factorial(n): # Base case if n == 0: return 1 # Recursive case return n * factorial(n - 1) # Driver Code if __name__ == '__main__': n = 4 print('Factorial of', n, 'is:', factorial(n))> C# using System; class Program { // Recursive Function to calculate Factorial of a number static int Factorial(int n) { // Base case if (n == 0) { return 1; } // Recursive case return n * Factorial(n - 1); } // Driver Code static void Main() { int n = 4; Console.WriteLine('Factorial of ' + n + ' is: ' + Factorial(n)); } }> Javascript // Function to calculate the factorial of a number using recursion function factorial(n) { // Base case: If n is 0, the factorial is 1. if (n === 0) { return 1; } // Recursive case: Calculate the factorial by multiplying n with the factorial of (n - 1). return n * factorial(n - 1); } // Main function function main() { // Given number let n = 4; // Calculate the factorial of n. let result = factorial(n); // Print the result console.log('Factorial of ' + n + ' is: ' + result); } // Call the main function main();> Výkon
Factorial of 4 is:24>
Časová zložitosť: O(n)
Pomocný priestor: O(n)
