V informatike existujú niektoré problémy, ktorých riešenia ešte nie sú nájdené, problémy sú rozdelené do tried tzv Triedy zložitosti . V teórii zložitosti je trieda zložitosti súborom problémov so súvisiacou zložitosťou. Tieto triedy pomáhajú vedcom zoskupovať problémy podľa toho, koľko času a priestoru potrebujú na vyriešenie problémov a overenie riešení. Je to odvetvie teórie výpočtov, ktoré sa zaoberá zdrojmi potrebnými na vyriešenie problému.
skontrolujte nulu v jazyku Java
Spoločnými zdrojmi sú čas a priestor, čo znamená, koľko času potrebuje algoritmus na vyriešenie problému a zodpovedajúce využitie pamäte.
- Časová zložitosť algoritmu sa používa na opis počtu krokov potrebných na vyriešenie problému, ale môže sa použiť aj na opis toho, ako dlho trvá overenie odpovede.
- Priestorová zložitosť algoritmu popisuje, koľko pamäte je potrebné na fungovanie algoritmu.
Triedy zložitosti sú užitočné pri organizovaní podobných typov problémov.
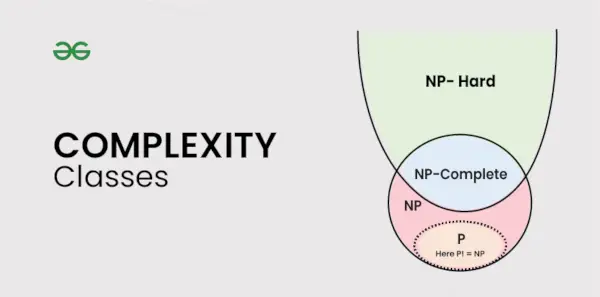
Typy tried zložitosti
Tento článok pojednáva o nasledujúcich triedach zložitosti:
- Trieda P
- Trieda NP
- Trieda CoNP
- NP-tvrdý
- NP-komplet
Trieda P
P v triede P znamená Polynomiálny čas. Je to súbor rozhodovacích problémov (problémy s odpoveďou áno alebo nie), ktoré môže vyriešiť deterministický stroj v polynomiálnom čase.
Vlastnosti:
- Riešenie na P problém s je ľahké nájsť.
- P je často triedou výpočtových problémov, ktoré sú riešiteľné a riešiteľné. Riešiteľné znamená, že problémy možno riešiť teoreticky aj prakticky. Ale problémy, ktoré možno vyriešiť teoreticky, ale nie v praxi, sú známe ako neriešiteľné.
Táto trieda obsahuje veľa problémov:
- Výpočet najväčšieho spoločného deliteľa.
- Nájdenie maximálnej zhody.
- Zlúčiť triedenie
Trieda NP
NP v triede NP znamená Nedeterministický polynomický čas . Je to súbor rozhodovacích problémov, ktoré môže vyriešiť nedeterministický stroj v polynomiálnom čase.
Vlastnosti:
- Riešenia triedy NP sa ťažko hľadajú, pretože ich rieši nedeterministický stroj, ale riešenia sa dajú ľahko overiť.
- Problémy NP môžu byť overené Turingovým strojom v polynomiálnom čase.
Príklad:
Pozrime sa na príklad, aby sme lepšie porozumeli triedy NP . Predpokladajme, že existuje spoločnosť, ktorá má celkom 1000 zamestnancov s jedinečným zamestnancom ID . Predpokladajme, že existujú 200 izby, ktoré majú k dispozícii. Výber z 200 zamestnanci musia byť spárovaní, ale generálny riaditeľ spoločnosti má údaje niektorých zamestnancov, ktorí z osobných dôvodov nemôžu pracovať v rovnakej miestnosti.
Toto je príklad an napr problém. Pretože je ľahké skontrolovať, či je daný výber 200 zamestnanci navrhnutí spolupracovníkom sú uspokojiví alebo nie, t. j. žiadny pár prevzatý zo zoznamu spolupracovníkov sa nenachádza na zozname, ktorý dal generálny riaditeľ. Ale vytvorenie takéhoto zoznamu od začiatku sa zdá byť také ťažké, že je úplne nepraktické.
java skener
Znamená to, že ak nám niekto môže poskytnúť riešenie problému, môžeme nájsť správnu a nesprávnu dvojicu v polynomiálnom čase. Teda pre napr triedny problém, odpoveď je možná, ktorá sa dá vypočítať v polynomiálnom čase.
Táto trieda obsahuje veľa problémov, ktoré by ste chceli vedieť efektívne vyriešiť:
- Booleovský problém uspokojiteľnosti (SAT).
- Problém hamiltonovskej cesty.
- Farbenie grafu.
Trieda Co-NP
Co-NP znamená doplnok triedy NP. To znamená, že ak je odpoveď na problém v Co-NP Nie, potom existuje dôkaz, ktorý možno skontrolovať v polynomiálnom čase.
Vlastnosti:
- Ak je problém X v NP, potom jeho doplnok X‘ je tiež v CoNP.
- Pre problém NP a CoNP nie je potrebné overiť všetky odpovede naraz v polynomiálnom čase, je potrebné overiť iba jednu konkrétnu odpoveď áno alebo nie v polynomiálnom čase, aby bol problém v NP alebo CoNP.
Niektoré príklady problémov pre CoNP sú:
- Na kontrolu prvočísla.
- Faktorizácia celých čísel.
NP-tvrdá trieda
NP-ťažký problém je prinajmenšom taký ťažký ako najťažší problém v NP a je to taká trieda problémov, že každý problém v NP sa redukuje na NP-ťažký.
Vlastnosti:
- Všetky NP-ťažké problémy nie sú v NP.
- Ich kontrola trvá dlho. To znamená, že ak je dané riešenie pre NP-ťažký problém, potom trvá dlho, kým sa skontroluje, či je správne alebo nie.
- Problém A je v NP-ťažký, ak pre každý problém L v NP existuje polynomiálna časová redukcia z L na A.
Niektoré z príkladov problémov v Np-hard sú:
- Problém zastavenia.
- Kvalifikované booleovské vzorce.
- Žiadny hamiltonovský cyklus.
NP-úplná trieda
Problém je NP-úplný, ak je NP aj NP-ťažký. NP-úplné problémy sú ťažké problémy v NP.
ostrý uhol
Vlastnosti:
- NP-úplné problémy sú špeciálne, pretože akýkoľvek problém v triede NP môže byť transformovaný alebo redukovaný na NP-úplné problémy v polynomiálnom čase.
- Ak by sa dal vyriešiť NP-úplný problém v polynomiálnom čase, potom by sa dal vyriešiť aj akýkoľvek NP problém v polynomiálnom čase.
Niektoré príklady problémov zahŕňajú:
- Hamiltonovský cyklus.
- Spokojnosť.
- Vertexový kryt .
| Trieda zložitosti | Charakteristický znak |
| P | Ľahko riešiteľné v polynomiálnom čase. |
| napr | Áno, odpovede je možné kontrolovať v polynomickom čase. |
| Co-NP | Nie, odpovede je možné kontrolovať v polynomickom čase. |
| NP-tvrdý | Všetky NP-ťažké problémy nie sú v NP a ich kontrola trvá dlho. |
| NP-komplet | Problém, ktorý je NP a NP-ťažký, je NP-úplný. |
