Moment zotrvačnosti je vlastnosťou telesa v rotačnom pohybe. Moment zotrvačnosti je vlastnosťou rotačných telies, ktorá má tendenciu brániť sa zmene rotačného pohybu telesa. Je to podobné ako zotrvačnosť akéhokoľvek telesa pri translačnom pohybe. Matematicky je moment zotrvačnosti daný ako súčet súčinu hmotnosti každej častice a štvorca vzdialenosti od rotačnej osi. Meria sa v jednotke kgm 2 .
Dozvieme sa podrobne o momente zotrvačnosti v článku nižšie.
Obsah
- Definícia momentu zotrvačnosti
- Formula Moment zotrvačnosti
- Faktory ovplyvňujúce moment zotrvačnosti
- Ako vypočítať moment zotrvačnosti?
- Vzorec momentu zotrvačnosti pre rôzne tvary
- Polomer otáčania
- Vety o momente zotrvačnosti
- Momenty zotrvačnosti pre rôzne predmety
Definícia momentu zotrvačnosti
Moment zotrvačnosti je tendencia telesa v rotačnom pohybe, ktorý bráni jeho zmene rotačný pohyb vplyvom vonkajších síl. Moment zotrvačnosti sa správa ako uhlová hmota a nazýva sa rotačná zotrvačnosť. Moment zotrvačnosti je analogický s mechanickým Zotrvačnosť tela.
MOI je definovaná ako množstvo vyjadrené súčtom súčinu omša každej častice so štvorcom jej vzdialenosti od osi rotácie pre akúkoľvek časticu vykonávajúcu rotačný pohyb.
Jednotka momentu zotrvačnosti
Moment zotrvačnosti je skalárna veličina a jednotka SI momentu zotrvačnosti je kgm 2 .
Rozmerný vzorec momentu zotrvačnosti
Pretože moment zotrvačnosti je daný ako súčin hmotnosti a štvorca vzdialenosti. Jeho rozmerový vzorec je daná súčinom rozmerového vzorca hmotnosti a druhej mocniny rozmerového vzorca dĺžky. Rozmerový vzorec momentu zotrvačnosti je, ML 2
Čo je zotrvačnosť?
Zotrvačnosť je vlastnosť hmoty, vďaka ktorej má tendenciu odolávať zmene stavu svojho pohybu. To znamená, že telo v pokoji sa snaží zostať v pokoji a odolávať akejkoľvek sile, ktorá sa ho pokúša uviesť do pohybu, a teleso v pohybe sa snaží pokračovať v pohybe a odolávať akejkoľvek sile, ktorá sa ho pokúša priviesť k zmene veľkosti jeho pohybu. Pokiaľ ide o množstvo, rovná sa maximálnej sile, ktorá sa snaží zmeniť svoj stav pohybu .
Naučiť sa viac o Zotrvačnosť .
Formula Moment zotrvačnosti
Moment zotrvačnosti je a skalárne množstvo . Matematicky sa súčin druhej mocniny hmotnosti častice a vzdialenosti od osi rotácie nazýva moment zotrvačnosti častice okolo osi rotácie.
Všeobecný vzorec na nájdenie momentu zotrvačnosti akéhokoľvek objektu je,
ja = Mr 2
kde,
m je hmotnosť objektu“
r je vzdialenosť od osi otáčania
Pre teleso pozostávajúce zo súvislých nekonečne malých častíc sa na výpočet momentu zotrvačnosti používa integrálna forma momentu zotrvačnosti.
I = ∫dl
Ja =
int_{0}^{M} r^2 dm
Moment zotrvačnosti sústavy častíc
Moment zotrvačnosti systému častíc je daný vzorcom,
I = ∑m i r i 2
kde,
r i je kolmá vzdialenosť ithčastica od osi
m i je hmotnosť ithčastica
Vyššie uvedená rovnica momentu zotrvačnosti hovorí, že moment zotrvačnosti pre systém častíc sa rovná súčtu súčinu hmotnosti každej častice a štvorca vzdialenosti od osi rotácie každej častice.
Pre obrázok uvedený nižšie
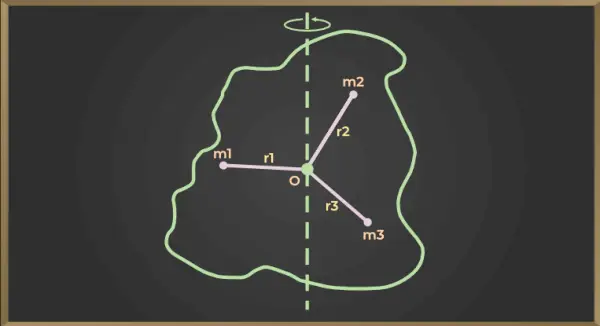
Moment zotrvačnosti prvej častice = m1×r12
Moment zotrvačnosti druhej častice = m2×r22
Moment zotrvačnosti tretej častice = m3×r32
podobne,
Moment zotrvačnosti nthčastica = mn×rn2
Teraz moment zotrvačnosti celého telesa okolo osi rotácie AB sa bude rovnať súčtu momentu zotrvačnosti všetkých častíc, takže
ja = m1×r12+ m2×r22+ m3×r32+……+mn×rn2
ako zakázať režim vývojára v systéme Android
I = Σm i ×r i 2
kde,
ja predstavujú moment zotrvačnosti telesa okolo osi otáčania
m i je hmotnosť ithčastica,
r i je polomer ithčastica
S predstavuje súčet.
Z rovnice môžeme povedať, že moment zotrvačnosti telesa okolo pevnej osi sa rovná súčtu súčinu hmotnosti každej častice tohto telesa a druhej mocniny jej kolmej vzdialenosti od pevnej osi.
Faktory ovplyvňujúce moment zotrvačnosti
Moment zotrvačnosti akéhokoľvek objektu závisí od nasledujúcich hodnôt:
- Tvar a veľkosť objektu
- Hustota materiálu objektu
- Os rotácie
Ako vypočítať moment zotrvačnosti?
Používa sa niekoľko spôsobov vypočítajte moment zotrvačnosti akéhokoľvek rotujúceho objektu.
- Pre rovnomerné objekty sa moment zotrvačnosti vypočíta tak, že sa zoberie súčin jeho hmotnosti so štvorcom jeho vzdialenosti od osi rotácie (r2).
- Pre nerovnomerné objekty vypočítame moment zotrvačnosti tak, že vezmeme súčet súčinu hmotnosti jednotlivých bodov na každom rôznom polomere, na tento účel sa použije vzorec
I = ∑m i r i 2
Vzorec momentu zotrvačnosti pre rôzne tvary
Táto tabuľka popisuje výrazy pre moment zotrvačnosti pre niektoré symetrické objekty spolu s ich osou rotácie:

| Objekt | Os | Vyjadrenie momentu zotrvačnosti |
|---|---|---|
| Dutý valec Tenkostenný | Centrálne | Ja = Mr2 |
| Tenký prsteň | Priemer | Ja = 1/2 Mr2 |
| Prstencový krúžok alebo dutý valec | Centrálne | I = 1/2 M(r22+ r12) |
| Pevný valec | Centrálne | Ja = 1/2 Mr2 |
| Jednotný disk | Priemer | Ja = 1/4 Mr2 |
| Dutá guľa | Centrálne | Ja = 2/3 Mr2 |
| Pevná guľa | Centrálne | Ja = 2/5 Mr2 |
| Jednotná symetrická sférická škrupina | Centrálne | |
| Jednotná doska alebo obdĺžnikový rovnobežník | Centrálne | I = 1/12 M (a2+ b2) |
| Tenká tyč | Centrálne | Ja = 1/12 Mr2 |
| Tenká tyč | Na konci Rod | Ja = 1/3 Mr2 |
Polomer otáčania
The Polomer otáčania telesa je definovaná ako kolmá vzdialenosť od osi rotácie k hmotnému bodu, ktorého hmotnosť sa rovná hmotnosti celého telesa a moment zotrvačnosti sa rovná skutočnému momentu zotrvačnosti objektu tak, ako bol predpokladalo, že je tam sústredená celková hmotnosť tela. Je to pomyselná vzdialenosť. Polomer otáčania je označený K.
Ak je hmotnosť a polomer otáčania telesa M a K, potom moment zotrvačnosti telesa je
Ja = MK 2 ……(1)
Polomer otáčania telesa je teda kolmý na os otáčania, ktorej štvorec vynásobený hmotnosťou tohto telesa udáva moment zotrvačnosti telesa okolo tejto osi.
Opäť podľa rovnice (1), K2= I/M
K = √ (I/m)
Polomer otáčania telesa okolo osi sa teda rovná druhej odmocnine pomeru telesa okolo tejto osi.
Vety o momente zotrvačnosti
Existujú dva typy teorémov, ktoré sú veľmi dôležité vzhľadom na moment zotrvačnosti:
- Veta o paralelnej osi
- Veta o kolmej osi
Veta o kolmej osi
Veta o kolmej osi uvádza, že súčet momentov zotrvačnosti telesa okolo dvoch vzájomne kolmých osí ležiacich v rovine telesa sa rovná momentu zotrvačnosti telesa okolo tretej osi, ktorá je kolmá na obe osi a prechádza ich bodom. križovatky.

Na obrázku vyššie VÔL a LTD sú dve osi v rovine telesa, ktoré sú na seba kolmé. Tretia os je OZ ktorá je kolmá na rovinu telesa a prechádza priesečníkom VÔL a LTD osi. Ak ja X , ja a , a ja S sú momenty zotrvačnosti telesa okolo osi VÔL , LTD , a OZ osí, potom podľa tejto vety
ja X + ja a = ja S
Veta o paralelnej osi
Podľa Veta o paralelnej osi , moment zotrvačnosti telesa okolo danej osi je súčet momentu zotrvačnosti okolo osi prechádzajúcej ťažiskom tohto telesa a súčinom druhej mocniny hmotnosti telesa a kolmej vzdialenosti medzi dve osi.
setinterval javascript

Nech vo vyššie uvedenom obrázku, musíme nájsť moment zotrvačnosti ja O telesa prechádzajúceho bodom O a okolo osi kolmej na rovinu, pričom moment zotrvačnosti telesa prechádzajúceho ťažiskom C a okolo osi rovnobežnej s danou osou je ja C , potom podľa tejto vety
ja O = ja C + Ml 2
kde
M je hmotnosť celého tela
l je kolmá vzdialenosť medzi dvoma osami.
Momenty zotrvačnosti pre rôzne predmety
Moment zotrvačnosti rôznych objektov je popísaný nižšie v tomto článku
Moment zotrvačnosti obdĺžnikovej dosky
Ak je hmotnosť dosky M, dĺžka l a šírka b, potom moment zotrvačnosti prechádza ťažiskom a okolo osi kolmej na rovinu dosky.

I = M(l 2 + b 2 / 12)
Moment zotrvačnosti disku
Ak má disk hmotnosť M a polomer r, potom moment zotrvačnosti okolo geometrickej osi disku je

I = 1/2 (Mr 2 )
Moment zotrvačnosti tyče
Ak je hmotnosť tyče M a dĺžka je l, potom moment zotrvačnosti okolo osi kolmej na dĺžku tyče a prechádzajúcej jej ťažiskom

I = ML 2 /12
Moment zotrvačnosti kruhu
Ak je hmotnosť krúžku M a polomer krúžku r, potom moment zotrvačnosti okolo osi prechádzajúcej kolmo k stredu krúžku je

Ja = Mr 2
Moment zotrvačnosti sféry
Ak má pevná guľa hmotnosť M a polomer r, potom moment zotrvačnosti okolo jej priemeru je

I = 2/5 Mr 2
Moment zotrvačnosti tuhého valca
Moment zotrvačnosti tuhého valca s polomerom „R“ a hmotnosťou M je daný vzorcom

I = 1/2MR 2
Moment zotrvačnosti dutého valca
Dutý valec má dva polomery, a to vnútorný polomer a vonkajší polomer. Moment zotrvačnosti dutého valca s hmotnosťou M, vonkajším polomerom R1a vnútorný polomer R2sa uvádza ako

I = 1/2 M (R 1 2 + R 2 2 )
Moment zotrvačnosti pevnej gule
Moment zotrvačnosti pevnej gule s hmotnosťou „M“ a polomerom „R“ je daný ako

I = 2/5MR 2
Moment zotrvačnosti dutej gule
Moment zotrvačnosti dutej gule s hmotnosťou M a polomerom „R“ je daný ako

I = 2/3MR 2
Moment zotrvačnosti prsteňa
Moment zotrvačnosti prstenca sa udáva pre dva prípady, keď os otáčania prechádza stredom a keď os otáčania prechádza priemerom.
Moment zotrvačnosti prstenca okolo osi prechádzajúcej stredom je daný
previesť reťazec na int

Ja = MR 2
Moment zotrvačnosti prstenca okolo osi prechádzajúcej priemerom je daný

Ja = Mr 2 /2
Moment zotrvačnosti námestia
Moment zotrvačnosti štvorca strany „a“ je daný ako

ja = a 4 /12
Moment zotrvačnosti štvorcovej dosky so stranou dĺžky „l“ a hmotnosti M je daný ako
I = 1/6 ml 2
Moment zotrvačnosti trojuholníka
Moment zotrvačnosti trojuholníka je daný pre 3 situácie, prvá, keď os prechádza stredom, druhá, keď os prechádza základňou a tretia, keď je os kolmá na základňu. Pozrime sa na vzorec pre nich jeden po druhom. Pre trojuholník so základňou „b“ a výškou „h“ je vzorec pre moment zotrvačnosti daný nasledovne

Keď os prejde cez ťažisko
I = bh 3 /36
Keď os prechádza cez základňu
I = bh 3 /12
Keď je os kolmá na základňu
I = (hb/36) (b 2 – b 1 b + b 1 2 )
Rozdiel medzi momentom zotrvačnosti a zotrvačnosťou
Rozdiel medzi zotrvačnosťou a momentom zotrvačnosti je uvedený v tabuľke nižšie:
| Áno nie. | Zotrvačnosť | Moment zotrvačnosti |
|---|---|---|
| 1. | Jeho význam je v lineárnom pohybe. | Jeho význam je v rotačnom pohybe. |
| 2. | Je to vlastnosť objektu, ktorá bráni zmene stavu objektu pri lineárnom pohybe. | Moment zotrvačnosti je vlastnosť objektu, ktorá bráni zmene stavu objektu pri rotačnom pohybe. |
| 3. | Zotrvačnosť objektu závisí iba od jeho hmotnosti. | Moment zotrvačnosti objektu závisí od jeho hmotnosti a jej rozloženia hmotnosti vzhľadom na os rotácie. |
| 4. | Zotrvačnosť objektu je pevná. | Moment zotrvačnosti objektu sa mení v závislosti od rôznych osí otáčania. |
Kinetická energia rotujúceho tela
Predpokladajme, že teleso s hmotnosťou „m“ rotujúce rýchlosťou v vo vzdialenosti „r“ od osi rotácie. Jeho uhlová rýchlosť je potom daná vzťahom ω = v/r, potom v = rω. Teraz vieme, že Kinetická energia tela je daný
KE = 1/2 mv 2
⇒ KE = 1/2 m(rω)2
⇒ KE = 1/2 mr2oh2
⇒ KE = 1/2Iω 2
Kinetická energia rotujúceho telesa je teda daná polovicou súčinu momentu zotrvačnosti a uhlová rýchlosť tela. Kinetická energia rotujúceho telesa sa tiež nazýva Rotačná kinetická energia . Vzorec rotačnej kinetickej energie je uvedený ako
KE = 1/2Iω 2
Moment zotrvačnosti (I) je nezávislý od uhlovej rýchlosti telesa. Je funkciou hmotnosti rotujúceho telesa a vzdialenosti telesa od osi rotácie. Preto pozorujeme, že uhlový pohyb je analogický s lineárnym pohybom, čo znamená, že význam momentu zotrvačnosti je v tom, že poskytuje predstavu o tom, ako sú hmoty rozložené v rôznych vzdialenostiach od osi rotácie v rotujúcom telese.
Aplikácia momentu zotrvačnosti
Moment of Inertia má rôzne aplikácie, z ktorých niektoré sú popísané nižšie:
- V dôsledku väčšieho momentu zotrvačnosti sa Zem otáča okolo svojej osi rovnakou uhlovou rýchlosťou.
- Malé pohyblivé koliesko je umiestnené pod detským motorčekom na hranie. Po otretí tohto kolesa o zem a opustení motora, v dôsledku momentu zotrvačnosti kolesa, motor ešte nejaký čas beží.
- Každý motor pozostáva z veľkého a ťažkého kolesa pripevneného k jeho hriadeľu, pričom väčšina jeho hmoty je na jeho obvode. Preto je jeho moment zotrvačnosti vysoký. Toto koleso sa nazýva zotrvačník. Krútiaci moment, ktorý poháňa hriadeľ motora, sa neustále zvyšuje. Preto rotácia hriadeľa nemusí byť rovnomerná, ale v dôsledku prítomnosti pohyblivého kolesa s väčšou zotrvačnosťou sa hriadeľ naďalej otáča takmer rovnomernou rýchlosťou.
- V kolese volských záprahov, rikší, kolobežiek, bicyklov atď. sa väčšina hmoty sústreďuje na jeho kruhu alebo ráfiku. táto obruč alebo rutina je pripevnená k osi kolesa pevnými lúčmi. Tým sa zvyšuje jeho moment zotrvačnosti. Preto, keď sa nohy počas bicyklovania prestanú hýbať, koleso sa ešte nejaký čas točí.
Tiež skontrolujte
- Kinematika rotačného pohybu
- Pohyb tuhého telesa
- Rolling Motion
Vyriešené príklady momentov zotrvačnosti
Príklad 1: Teleso s hmotnosťou 500 g sa otáča okolo osi. vzdialenosť ťažiska telesa od osi otáčania je 1,2 m. nájdite moment zotrvačnosti telesa okolo osi otáčania.
Riešenie:
Vzhľadom na to, že M = 500 g = 0,5 kg, r = 1,2 m.
Je zrejmé, že sa dá predpokladať, že celá hmotnosť telesa je umiestnená v jeho ťažisku. Potom moment zotrvačnosti telesa okolo osi otáčania.
Ja = Mr2
I = 0,5 × (1,2)2
I = 0,72 kg m2
Príklad 2: Polomer otáčania okolo osi vzdialenej 12 cm od ťažiska telesa s hmotnosťou 1,2 kg je 13 cm. Vypočítajte polomer otáčania a moment zotrvačnosti okolo osi prechádzajúcej ťažiskom.
Riešenie:
Vzhľadom na to, že M = 1,0 kg, K = 13 cm, l = 12 cm, KCM= ?, jaCM= ?
java s hojdačkouZ vety o rovnobežnej osi I = ICM+ Ml2
K2= KCM2+ l2
alebo KCM2= K2– l2
KCM2 = (13)2– (12)2= 25
KCM= 5
Teraz moment zotrvačnosti ICM= MKCM2
jaCM= 1,0 × (0,05)2= 2,5 x 10-3kg m2
Príklad 3: Teleso s hmotnosťou 0,1 kg sa otáča okolo osi. ak je vzdialenosť ťažiska telesa od osi otáčania 0,5 m, potom nájdite moment zotrvačnosti telesa.
Riešenie:
Vzhľadom na to, že M = 0,1 kg a r = 0,5 m
takže ja = Mr2
I = 0,1 × (0,5)2
I = 0,025 kg m2
Príklad 4: Moment zotrvačnosti krúžkov okolo osi prechádzajúcej jeho stredom kolmo na rovinu kruhového krúžku je 200 gm cm 2 . Aký bude moment zotrvačnosti jeho priemeru?
Riešenie:
Moment zotrvačnosti kruhového prstenca okolo osi prechádzajúcej iným stredom kolmým na jeho rovinu
PÁN2= 200 g cm2
Moment zotrvačnosti okolo priemeru
= 1/2 MR2
= 1/2 x 200 = 100 gm cm2
Časté otázky o momentoch zotrvačnosti
Ako vypočítať moment zotrvačnosti?
Základný vzorec na nájdenie momentu zotrvačnosti akéhokoľvek rovnomerného objektu je,
ja = Mr 2
kde,
m je hmotnosť objektu“
r je vzdialenosť od osi otáčania
Ako vypočítať moment zotrvačnosti lúča?
Moment zotrvačnosti lúča pozdĺž stredu a horizontálnej osi sa vypočíta pomocou vzorca,
I = ML 2 / 12
Od čoho závisí moment zotrvačnosti telesa?
Moment zotrvačnosti akéhokoľvek objektu závisí od faktorov uvedených nižšie:
- Hmotnosť tela,
- Os otáčania
- Tvar a veľkosť objektu
Čo je to jednotka momentu zotrvačnosti?
Jednotkou momentu zotrvačnosti je kgm 2
Môže byť moment zotrvačnosti negatívny?
Nie, moment zotrvačnosti nemôže byť nikdy negatívny.
Čo je to hmotnostný moment zotrvačnosti?
Hmotnostný moment zotrvačnosti je meranie odporu telesa voči zmene jeho momentu hybnosti alebo smeru. Hmotnostný moment zotrvačnosti pre hmotu bodu je daný vzťahom I = mr2a pre systém častíc je hmotnostný moment zotrvačnosti daný ako I = Σimiri2
Čo je to plošný moment zotrvačnosti?
Plošný moment zotrvačnosti je vlastnosť roviny 2D tvaru, ktorá ukazuje, ako sú body rozptýlené vzhľadom na ľubovoľnú os v rovine. Plošný moment zotrvačnosti je známy aj ako druhý moment plochy alebo kvadratický moment plochy. Vzorec pre plošný moment zotrvačnosti v rovine xy je daný ako Ixy= ∫xy dxdxy = ∫xy dA
