Aritmetická hodnota, ktorá sa používa na vyjadrenie množstva a používa sa pri výpočtoch, sú definované ako čísla. Symbol ako 4, 5, 6, ktorý predstavuje číslo, je známy ako číslica. Bez čísel nemôžeme robiť počítanie vecí, dátumu, času, peňazí atď., Tieto čísla sa používajú aj na meranie a označovanie.

Vďaka vlastnostiam čísel sú užitočné pri vykonávaní aritmetických operácií s nimi. Tieto čísla môžu byť zapísané v číselných tvaroch a tiež slovami.

Napríklad , 3 sa píše ako tri slovami, 35 sa píše ako tridsaťpäť slov atď. Študenti môžu napísať čísla od 1 do 100 slovami, aby sa dozvedeli viac.

Existujú rôzne typy čísel, ktoré sa môžeme naučiť. Sú to celé a prirodzené čísla, nepárne a párne čísla, racionálne a iracionálne čísla atď.

Čo je číselná sústava?

Číselná sústava je metóda zobrazovania čísel písaním, čo je matematický spôsob reprezentácie čísel danej množiny, pomocou čísel alebo symbolov matematickým spôsobom. Systém písania na označovanie čísel pomocou číslic alebo symbolov logickým spôsobom je definovaný ako číselný systém.

Na vytvorenie všetkých čísel môžeme použiť číslice od 0 do 9. S týmito číslicami môže každý vytvoriť nekonečné čísla.

Napríklad 156, 3907, 3456, 1298, 784859 atď.

Čo je druhá odmocnina?

Hodnota počtu druhých odmocnín, ktorá pri vynásobení sama osebe dáva pôvodné číslo. Predpokladajme, že a je druhá odmocnina z b, potom je vyjadrená ako a = √b alebo môžeme vyjadriť rovnakú rovnicu ako a2 = b. Tu sa „√“ tento symbol, ktorý sme použili na vyjadrenie koreňa čísel, označuje ako radikál. Kladné číslo, keď sa má vynásobiť samo o sebe, predstavuje druhú mocninu čísla. Druhá odmocnina z akéhokoľvek kladného čísla dáva pôvodné číslo.

Napríklad, štvorec 4 je 16, 4²= 16 a druhá odmocnina z 16, √16 = 4. Keďže 4 je dokonalý štvorec, je ľahké nájsť druhú odmocninu takýchto čísel, ale pre nedokonalú druhú mocninu je to naozaj zložité.

Druhá odmocnina je reprezentovaná ako '√' Hovorí sa tomu radikálny symbol. Na vyjadrenie čísla „a“ ako druhej odmocniny pomocou tohto symbolu možno napísať ako: „√a“, kde a je číslo.

rozdiel medzi gigabajtom a megabajtom

Číslo pod symbolom radikálu sa nazýva radikand. Napríklad druhá odmocnina 4 je tiež reprezentovaná ako radikál 4. Obidva predstavujú rovnakú hodnotu.

Vzorec na nájdenie druhej odmocniny je: a = √b

Vlastnosti druhej odmocniny

Je definovaná ako funkcia jedna ku jednej, ktorá berie kladné číslo ako vstup a vracia druhú odmocninu daného vstupného čísla.

f(x) = √x

Napríklad, ak x = 9, funkcia vráti výstupnú hodnotu ako 3.

Vlastnosti druhej odmocniny sú nasledovné:

10 zo 100

• Ak je číslo dokonalé druhé číslo, potom určite existuje dokonalá odmocnina.
• Ak číslo končí párnym počtom núl (0), potom môžeme mať druhú odmocninu.
• Dve druhé odmocniny možno vynásobiť. Napríklad √3 možno vynásobiť √2, potom bude výsledok √6.
• Keď sa vynásobia dve rovnaké odmocniny, výsledkom musí byť radikálne číslo. Ukazuje, že výsledkom je číslo bez druhej odmocniny. Napríklad, keď sa √7 vynásobí √7, získaný výsledok je 7.
• Druhá odmocnina záporných čísel nie je definovaná. Preto dokonalý štvorec nemôže byť záporný.
• Niektoré čísla končia 2, 3, 7 alebo 8 (v jednotkovej číslici), potom dokonalá druhá odmocnina neexistuje.
• Niektoré čísla končia 1, 4, 5, 6 alebo 9 v jednotkovej číslici, potom bude mať číslo druhú odmocninu.

Je ľahké nájsť druhú odmocninu čísla, ktoré je dokonalým druhou mocninou.

Perfektné štvorce sú tie kladné čísla, ktoré možno zapísať ako násobenie čísla samého osebe, alebo môžete povedať, že dokonalý štvorec je číslo, ktoré je hodnotou mocniny 2 ľubovoľného celého čísla.

Číslo, ktoré možno vyjadriť ako súčin dvoch rovnakých celých čísel. Napríklad 16 je dokonalý štvorec, pretože je súčinom dvoch rovnakých celých čísel, 4 × 4 = 16. Avšak 24 nie je dokonalý štvorec, pretože ho nemožno vyjadriť ako súčin dvoch rovnakých celých čísel. (8 x 3 = 24).

Číslo, ktoré sa získa umocnením celého čísla, sa nazýva dokonalý štvorec.

Ak predpokladáme, že N je dokonalý štvorec celého čísla y, môžeme to zapísať ako N = súčin y a y = y².

Takže vzorec dokonalého štvorca môže byť vyjadrený ako:

N = Y ²

Použime vzorec s hodnotami:

Ak y = 9 a N = y²

To znamená, že N = 9²= 81.

Tu je 81 dokonalá druhá mocnina 9, pretože je druhou mocninou celého čísla.

typy cyklu for

Pomocou druhých odmocnín vieme identifikovať, či je číslo dokonalou druhou mocninou alebo nie, ak vypočítame druhú odmocninu daného čísla.

Ak je druhá odmocnina celé číslo, potom dané číslo bude dokonalou druhou mocninou, a ak hodnota druhej odmocniny nie je celé číslo, potom dané číslo nie je dokonalou druhou mocninou.

napr. aby sme skontrolovali, či 24 je dokonalá druhá mocnina alebo nie, vypočítame jej druhú odmocninu. √24 = 4,898979. Ako vidíme, 4,898979 nie je celé číslo, takže 24 nie je dokonalý štvorec.

Zoberme si ďalší príklad

Číslo 49. √49 = 7. Vidíme, že 7 je celé číslo, preto je 49 dokonalý štvorec.

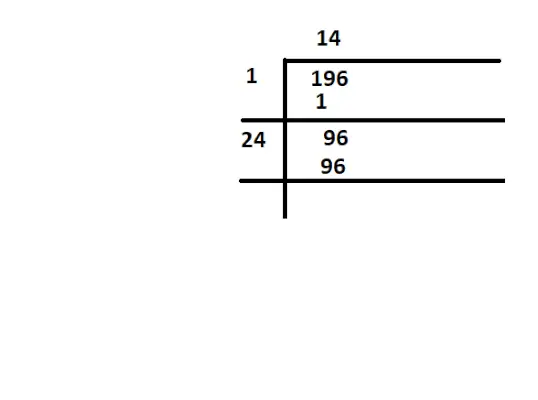
Je 196 Perfect Square?

Riešenie:

Aby sme skontrolovali, či je 196 dokonalý štvorec, musíme nájsť druhé odmocniny čísla 196

dokonalý štvorec 196

príkaz java return

Tu je druhá odmocnina z 196 14

Dokonalé štvorce sú tie kladné čísla, ktoré možno zapísať ako násobenie čísla samy osebe, alebo môžete povedať, že dokonalý štvorec je číslo, ktoré je hodnotou mocniny 2 akéhokoľvek celého čísla.

Tu môžeme napísať √196 = 14 alebo 14²= 14 × 14 = 196.

Preto je 196 dokonalý štvorec.

Podobné otázky

Otázka 1: Aká je druhá odmocnina z 625?

Riešenie:

dokonalý štvorec 625

pytónový had vs anakonda

tu 625 je dokonalý štvorec 25

Takže môžeme písať ako √625 = 25 alebo 25²= 25 × 25 = 625

Otázka 2: Ako zistíte druhú odmocninu z 24?

Riešenie:

druhá odmocnina z 24

Tu 24 nie je dokonalý štvorec 4,8989.

Preto √24 = 4,8989..

Otázka 3: Nájdite druhú odmocninu z 361?

Riešenie:

štvorec 361

Tu druhá odmocnina z 361 je 19 , celé číslo, ktoré je dokonalým štvorcom

Preto √361 = 19 alebo 19²= 19 × 19 = 361