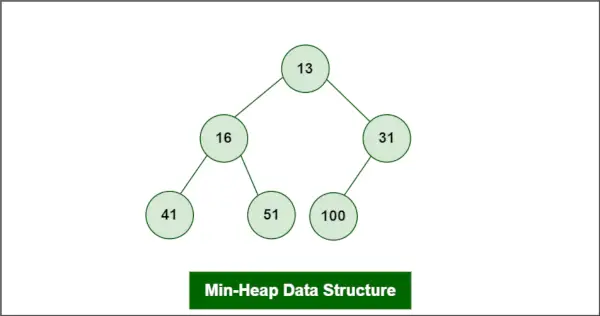
A Min-Hroma je definovaný ako typ Štruktúra údajov haldy je typ binárneho stromu, ktorý sa bežne používa v informatike na rôzne účely vrátane triedenia, vyhľadávania a organizovania údajov.
Úvod do Min-Heap – Štruktúra údajov a návody na algoritmy
Účel a prípady použitia minimálnej haldy:
- Implementácia prioritného frontu: Jedným z primárnych použití štruktúry údajov haldy je implementácia prioritných frontov.
- Dijkstrov algoritmus : Dijkstrov algoritmus je algoritmus najkratšej cesty, ktorý nájde najkratšiu cestu medzi dvoma uzlami v grafe. Na sledovanie nenavštívených uzlov s najmenšou vzdialenosťou od zdrojového uzla možno použiť minimálnu haldu.
- Triedenie: Minimálna halda môže byť použitá ako triediaci algoritmus na efektívne triedenie kolekcie prvkov vo vzostupnom poradí.
- Stredný nález: Na efektívne nájdenie mediánu toku čísel možno použiť minimálnu hromadu. Na uloženie väčšej polovice čísel môžeme použiť jednu minovú kopu a na uchovanie menšej polovice jednu maximálnu kopu. Medián bude koreňom minimálnej haldy.
Štruktúra údajov Min-Heap v rôznych jazykoch:
1. Min-Heap v C++
Minimálna halda môže byť implementovaná pomocou prioritný_front kontajnera zo štandardnej knižnice šablón (STL). The prioritný_front kontajner je typ adaptéra kontajnera, ktorý poskytuje spôsob ukladania prvkov do dátovej štruktúry podobnej frontu, v ktorej má každý prvok priradenú prioritu.
Syntax :
C++ priority_queue < int, vector , väčší > minH;>
2. Min-Heap v Jave
V Jave môže byť min halda implementovaná pomocou PriorityQueue triedy od balík java.util . Trieda PriorityQueue je prioritný front, ktorý poskytuje spôsob ukladania prvkov do dátovej štruktúry podobnej frontu, v ktorej má každý prvok priradenú prioritu.
Syntax :
Java PriorityQueue minHeap = nový PriorityQueue ();>
3. Min-Heap v Pythone
V Pythone je možné implementovať minimálnu haldu pomocou heapq modul, ktorý poskytuje funkcie na implementáciu hromady. Konkrétne, heapq modul poskytuje spôsob vytvárania a manipulácie s dátovými štruktúrami haldy.
Syntax:
Python heap = [] heapify(heap)>
4. Minimálna hromada v C#
V C# môže byť minimálna halda implementovaná pomocou triedy PriorityQueue z System.Collections.Generic namespace . Trieda PriorityQueue je prioritný front, ktorý poskytuje spôsob ukladania prvkov do dátovej štruktúry podobnej frontu, v ktorej má každý prvok priradenú prioritu.
Syntax:
C# var minHeap = new PriorityQueue ();>
5. Min-hromada v JavaScripte
Min halda je binárny strom, kde každý uzol má hodnotu menšiu alebo rovnú svojim potomkom. V JavaScripte môžete implementovať minimálnu haldu pomocou poľa, kde prvý prvok predstavuje koreňový uzol a potomkovia uzla na indexe i sa nachádzajú na indexoch 2i+1 a 2i+2.
Syntax:
JavaScript const minHeap = new MinHeap();>
Rozdiel medzi minimálnou a maximálnou haldou:
|
| Min. halda | Max Heap |
|---|---|---|
| 1. | V Min-Heap kľúč prítomný v koreňovom uzle musí byť menší alebo rovný medzi kľúčmi prítomnými u všetkých jeho potomkov. | V Max-Heap kľúč prítomný v koreňovom uzle musí byť väčší alebo rovný medzi kľúčmi prítomnými vo všetkých jeho potomkoch. |
| 2. | V Min-Heap je minimálny kľúčový prvok prítomný v koreňovom adresári. | V Max-Heap je maximálny kľúčový prvok prítomný v koreňovom adresári. |
| 3. | Min-Heap používa vzostupnú prioritu. | Max-Heap používa zostupnú prioritu. |
| 4. | Pri konštrukcii min-hromady má prednosť najmenší prvok. | Pri konštrukcii Max-Heap má prednosť najväčší prvok. |
| 5. | V Min-Heap je najmenší prvok prvý, ktorý sa vysype z haldy. | V Max-Heap je najväčší prvok prvý, ktorý sa vysype z haldy. |
Interná implementácia dátovej štruktúry Min-Heap:
A Minimálna halda je zvyčajne reprezentovaná ako pole .
- Koreňový prvok bude v Arr[0] .
- Pre akýkoľvek i-tý uzol Arr[i] :
- Arr[(i -1) / 2] vráti svoj nadradený uzol.
- Arr[(2 * i) + 1] vráti svoj ľavý podriadený uzol.
- Arr[(2 * i) + 2] vráti svoj pravý podriadený uzol.
Vnútorná implementácia Min-Heap vyžaduje 3 hlavné kroky:
- Vkladanie : Ak chcete vložiť prvok na minimálnu haldu, najprv pripojíme prvok na koniec poľa a potom upravíme vlastnosť haldy opakovaným prehodením prvku s jeho rodičom, kým nebude v správnej polohe.
- Vymazanie : Ak chcete odstrániť minimálny prvok z minimálnej hromady, najprv zameníme koreňový uzol s posledným prvkom v poli, odstránime posledný prvok a potom upravíme vlastnosť haldy opakovaným prehodením prvku s jeho najmenším potomkom, kým nebude v poli správna poloha.
- Heapify : Operáciu heapify možno použiť na vytvorenie minimálnej haldy z nezoradeného poľa.
Operácie na dátovej štruktúre min-haldy a ich implementácia:
Tu sú niektoré bežné operácie, ktoré možno vykonať na dátovej štruktúre haldy,
1. Vloženie do dátovej štruktúry Min-Heap :
Prvky môžu byť vložené do haldy podobným prístupom, ako je uvedené vyššie pre vymazanie. Cieľom je:
- Operácia vloženia do mini-hromady zahŕňa nasledujúce kroky:
- Pridajte nový prvok na koniec haldy na ďalšiu dostupnú pozíciu v poslednej úrovni stromu.
- Porovnajte nový prvok s jeho nadradeným prvkom. Ak je nadradený prvok väčší ako nový prvok, vymeňte ich.
- Opakujte krok 2, kým rodič nebude menší alebo rovný novému prvku, alebo kým nový prvok nedosiahne koreň stromu.
- Nový prvok je teraz na svojej správnej pozícii v min halde a vlastnosť haldy je splnená.
Ilustrácia:
Predpokladajme, že halda je minimálna halda ako:
Vloženie do Min-Heap
Implementácia operácie vkladania v Min-Heap:
C++ #include #include using namespace std; // Function to insert a new element into the min-heap void insert_min_heap(vector & halda, int hodnota) { // Pridanie nového prvku na koniec haldy.push_back(value); // Získanie indexu posledného prvku int index = heap.size() - 1; // Porovnajte nový prvok s jeho rodičom a v prípade potreby ho zameňte while (index> 0 && heap[(index - 1) / 2]> heap[index]) { swap(heap[index], heap[(index - 1) / 2]); // Presun nahor v strome na rodiča aktuálneho // prvku index = (index - 1) / 2; } } // Hlavná funkcia na testovanie funkcie insert_min_heap int main() { vector hromada; hodnoty int[] = { 10, 7, 11, 5, 4, 13 }; int n = sizeof(hodnoty) / sizeof(hodnoty[0]); pre (int i = 0; i< n; i++) { insert_min_heap(heap, values[i]); cout << 'Inserted ' << values[i] << ' into the min-heap: '; for (int j = 0; j < heap.size(); j++) { cout << heap[j] << ' '; } cout << endl; } return 0; }>
Java import java.util.*; public class GFG { // Function to insert a new element into the min-heap public static void insertMinHeap(int[] heap, int size, int value) { // Add the new element to the end of the heap heap[size] = value; // Get the index of the last element int index = size; // Compare the new element with its parent and swap // if necessary while (index>0 && halda[(index - 1) / 2]> halda[index]) { swap(hromada, index, (index - 1) / 2); // Presun nahor v strome na rodiča aktuálneho // prvku index = (index - 1) / 2; } } // Funkcia na výmenu dvoch prvkov v poli public static void swap(int[] arr, int i, int j) { int temp = arr[i]; arr[i] = arr[j]; arr[j] = teplota; } // Hlavná funkcia na testovanie funkcie insertMinHeap public static void main(String[] args) { int[] halda = new int[6]; hodnoty int[] = { 10, 7, 11, 5, 4, 13 }; int veľkosť = 0; pre (int i = 0; i< values.length; i++) { insertMinHeap(heap, size, values[i]); size++; System.out.print('Inserted ' + values[i] + ' into the min-heap: '); for (int j = 0; j < size; j++) { System.out.print(heap[j] + ' '); } System.out.println(); } } }> Python3 def insert_min_heap(heap, value): # Add the new element to the end of the heap heap.append(value) # Get the index of the last element index = len(heap) - 1 # Compare the new element with its parent and swap if necessary while index>0 a halda[(index - 1) // 2]> halda[index]: halda[index], halda[(index - 1) // 2] = halda[(index - 1) // 2], halda[ index] # Posunúť sa v strome nahor na rodiča aktuálneho prvku index = (index - 1) // 2 halda = [] hodnoty = [10, 7, 11, 5, 4, 13] pre hodnotu v hodnotách: insert_min_heap( halda, hodnota) print(f'Vložené {value} do min-hromady: {heap}')> C# using System; using System.Collections.Generic; public class Program { // Function to insert a new element into the min-heap static void InsertMinHeap(List halda, int hodnota) { // Pridanie nového prvku na koniec haldy.Add(value); // Získanie indexu posledného prvku int index = heap.Count - 1; // Porovnajte nový prvok s jeho rodičom a // v prípade potreby zameňte while (index> 0 && heap[(index - 1) / 2]> heap[index]) { int temp = heap[index]; halda[index] = halda[(index - 1) / 2]; halda[(index - 1) / 2] = teplota; // Presun nahor v strome na rodiča aktuálneho // prvku index = (index - 1) / 2; } } // Hlavná funkcia na testovanie funkcie InsertMinHeap public static void Main() { List halda = nový Zoznam (); hodnoty int[] = { 10, 7, 11, 5, 4, 13 }; foreach(int hodnota v hodnotách) { InsertMinHeap(hromada, hodnota); Console.Write('Vložené ' + hodnota + ' do min-hromady: '); foreach(prvok int v halde) { Console.Write(element + ' '); } Console.WriteLine(); } } }> Javascript function insertMinHeap(heap, value) { heap.push(value); let index = heap.length - 1; let parentIndex = Math.floor((index - 1) / 2); while (index>0 && halda[parentIndex]> halda[index]) { [hromada[index], halda[parentIndex]] = [hromada[parentIndex], halda[index]]; index = parentIndex; parentIndex = Math.floor((index - 1) / 2); } } // Príklad použitia const heap = []; konštantné hodnoty = [10, 7, 11, 5, 4, 13]; for (konšt. hodnota hodnôt) { insertMinHeap(halda, hodnota); console.log(`Vložené ${value} do min-hromady: ${heap}`); }> Výkon
Inserted 10 into the min-heap: 10 Inserted 7 into the min-heap: 7 10 Inserted 11 into the min-heap: 7 10 11 Inserted 5 into the min-heap: 5 7 11 10 Inserted 4 into the min-heap: 4 5 11 10 7 Inser...>
Časová zložitosť: O(log(n)) ( kde n je počet prvkov v halde )
Pomocný priestor: O(n)
2. Vymazanie v dátovej štruktúre Min-Heap :
Odstránenie najmenšieho prvku (koreň) z min. Koreň je nahradený posledným prvkom v halde a potom sa vlastnosť haldy obnoví zámenou nového koreňa s jeho najmenším potomkom, kým rodič nie je menší ako oba potomkovia alebo kým nový koreň nedosiahne listový uzol.
- Nahraďte koreň alebo prvok, ktorý sa má odstrániť, posledným prvkom.
- Odstráňte posledný prvok z haldy.
- Keďže posledný prvok je teraz umiestnený na pozícii koreňového uzla. Takže nemusí nasledovať vlastnosť haldy. Preto navŕšte posledný uzol umiestnený na pozícii koreňa.
Ilustračné :
Predpokladajme, že halda je minimálna halda ako:
Štruktúra údajov minimálnej haldy
Prvok, ktorý sa má odstrániť, je root, t.j. 13.
Proces :
Posledný prvok je 100.
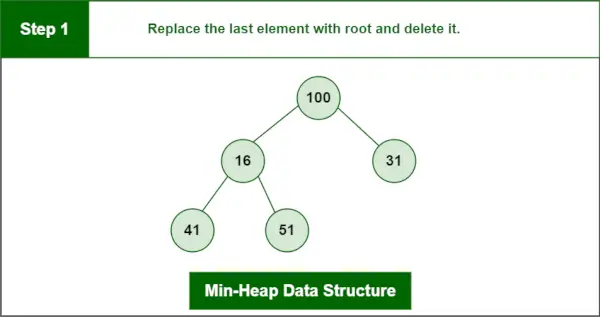
Krok 1: Nahraďte posledný prvok rootom a odstráňte ho.
Štruktúra údajov minimálnej haldy
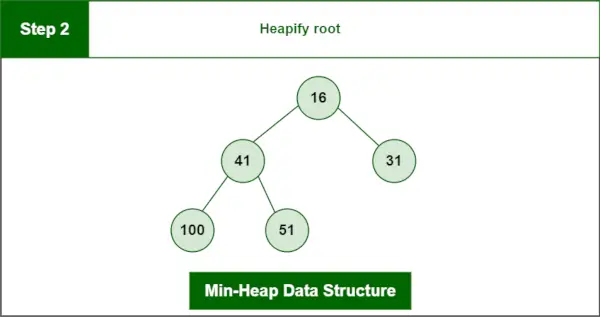
Krok 2 : Heapify root.
Konečná halda:
Štruktúra údajov minimálnej haldy
Implementácia operácie vymazania v Min-Heap:
C++ #include #include using namespace std; // Function to insert a new element into the min-heap void insert_min_heap(vector & halda, int hodnota) { // Pridanie nového prvku na koniec haldy.push_back(value); // Získanie indexu posledného prvku int index = heap.size() - 1; // Porovnajte nový prvok s jeho rodičom a v prípade potreby ho zameňte while (index> 0 && heap[(index - 1) / 2]> heap[index]) { swap(heap[index], heap[(index - 1) / 2]); // Presun nahor v strome na rodiča aktuálneho // prvku index = (index - 1) / 2; } } // Funkcia na vymazanie uzla z min-heap void delete_min_heap(vector & halda, hodnota int) { // Nájdenie indexu prvku, ktorý sa má odstrániť int index = -1; pre (int i = 0; i< heap.size(); i++) { if (heap[i] == value) { index = i; break; } } // If the element is not found, return if (index == -1) { return; } // Replace the element to be deleted with the last // element heap[index] = heap[heap.size() - 1]; // Remove the last element heap.pop_back(); // Heapify the tree starting from the element at the // deleted index while (true) { int left_child = 2 * index + 1; int right_child = 2 * index + 2; int smallest = index; if (left_child < heap.size() && heap[left_child] < heap[smallest]) { smallest = left_child; } if (right_child < heap.size() && heap[right_child] < heap[smallest]) { smallest = right_child; } if (smallest != index) { swap(heap[index], heap[smallest]); index = smallest; } else { break; } } } // Main function to test the insert_min_heap and // delete_min_heap functions int main() { vector hromada; hodnoty int[] = { 13, 16, 31, 41, 51, 100 }; int n = sizeof(hodnoty) / sizeof(hodnoty[0]); pre (int i = 0; i< n; i++) { insert_min_heap(heap, values[i]); } cout << 'Initial heap: '; for (int j = 0; j < heap.size(); j++) { cout << heap[j] << ' '; } cout << endl; delete_min_heap(heap, 13); cout << 'Heap after deleting 13: '; for (int j = 0; j < heap.size(); j++) { cout << heap[j] << ' '; } cout << endl; return 0; }>
Java import java.util.*; public class GFG { // Function to insert a new element into the min-heap public static void insertMinHeap(List halda, int hodnota) { // Pridanie nového prvku na koniec haldy haldy.add(value); // Získanie indexu posledného prvku int index = heap.size() - 1; // Porovnajte nový prvok s jeho rodičom a v prípade potreby ho swapujte while (index> 0 && heap.get((index - 1) / 2)> heap.get(index)) { Collections.swap(halda, index, (index - 1) / 2); // Presun nahor v strome na rodiča aktuálneho // prvku index = (index - 1) / 2; } } // Funkcia na vymazanie uzla z min-heap public static void deleteMinHeap(List halda, int hodnota) { // Nájdenie indexu prvku, ktorý sa má vymazať int index = -1; pre (int i = 0; i< heap.size(); i++) { if (heap.get(i) == value) { index = i; break; } } // If the element is not found, return if (index == -1) { return; } // Replace the element to be deleted with the last // element heap.set(index, heap.get(heap.size() - 1)); // Remove the last element heap.remove(heap.size() - 1); // Heapify the tree starting from the element at the // deleted index while (true) { int leftChild = 2 * index + 1; int rightChild = 2 * index + 2; int smallest = index; if (leftChild < heap.size() && heap.get(leftChild) < heap.get(smallest)) { smallest = leftChild; } if (rightChild < heap.size() && heap.get(rightChild) < heap.get(smallest)) { smallest = rightChild; } if (smallest != index) { Collections.swap(heap, index, smallest); index = smallest; } else { break; } } } // Main function to test the insertMinHeap and // deleteMinHeap functions public static void main(String[] args) { List halda = nový ArrayList (); hodnoty int[] = { 13, 16, 31, 41, 51, 100 }; int n = hodnoty.dĺžka; pre (int i = 0; i< n; i++) { insertMinHeap(heap, values[i]); } System.out.print('Initial heap: '); for (int j = 0; j < heap.size(); j++) { System.out.print(heap.get(j) + ' '); } System.out.println(); deleteMinHeap(heap, 13); System.out.print('Heap after deleting 13: '); for (int j = 0; j < heap.size(); j++) { System.out.print(heap.get(j) + ' '); } System.out.println(); } }> Python3 def insert_min_heap(heap, value): heap.append(value) index = len(heap) - 1 while index>0 a halda[(index - 1) // 2]> halda[index]: halda[index], halda[(index - 1) // 2] = halda[(index - 1) // 2], halda[ index] index = (index - 1) // 2 def delete_min_heap(hromada, hodnota): index = -1 pre i v rozsahu(len(hromada)): if heap[i] == hodnota: index = i break if index == -1: návrat haldy[index] = halda[-1] heap.pop() while True: left_child = 2 * index + 1 right_child = 2 * index + 2 najmenšie = index, ak left_child< len(heap) and heap[left_child] < heap[smallest]: smallest = left_child if right_child < len(heap) and heap[right_child] < heap[smallest]: smallest = right_child if smallest != index: heap[index], heap[smallest] = heap[smallest], heap[index] index = smallest else: break heap = [] values = [13, 16, 31, 41, 51, 100] for value in values: insert_min_heap(heap, value) print('Initial heap:', heap) delete_min_heap(heap, 13) print('Heap after deleting 13:', heap)> C# using System; using System.Collections.Generic; class MinHeap { private List halda = nový Zoznam (); public void Insert(int value) { heap.Add(value); int index = halda.Pocet - 1; while (index> 0 && halda[(index - 1) / 2]> halda[index]) { Swap(index, (index - 1) / 2); index = (index - 1) / 2; } } public void Delete(int hodnota) { int index = halda.IndexOf(hodnota); if (index == -1) { return; } halda[index] = halda[hromada.Pocet - 1]; heap.RemoveAt(heap.Count - 1); while (true) { int leftChild = 2 * index + 1; int rightChild = 2 * index + 2; int najmenší = index; ak (vľavoDieťa< heap.Count && heap[leftChild] < heap[smallest]) { smallest = leftChild; } if (rightChild < heap.Count && heap[rightChild] < heap[smallest]) { smallest = rightChild; } if (smallest != index) { Swap(index, smallest); index = smallest; } else { break; } } } private void Swap(int i, int j) { int temp = heap[i]; heap[i] = heap[j]; heap[j] = temp; } public void Print() { for (int i = 0; i < heap.Count; i++) { Console.Write(heap[i] + ' '); } Console.WriteLine(); } } class Program { static void Main(string[] args) { MinHeap heap = new MinHeap(); int[] values = { 13, 16, 31, 41, 51, 100 }; for (int i = 0; i < values.Length; i++) { heap.Insert(values[i]); } Console.Write('Initial heap: '); heap.Print(); heap.Delete(13); Console.Write('Heap after deleting 13: '); heap.Print(); } }> Javascript function insertMinHeap(heap, value) { // Add the new element to the end of the heap heap.push(value); // Get the index of the last element let index = heap.length - 1; // Compare the new element with its parent and swap if necessary for (let flr = Math.floor((index - 1) / 2); index>0 && halda[flr]> halda[index]; flr = Math.floor((index - 1) / 2)) { [hromada[index], halda[flr]] = [ halda[flr], halda[index], ]; // Presun v strome nahor na rodiča aktuálneho prvku index = Math.floor((index - 1) / 2); } } function deleteMinHeap(heap, value) { // Nájdenie indexu prvku, ktorý sa má vymazať nech index = -1; pre (nech i = 0; i< heap.length; i++) { if (heap[i] == value) { index = i; break; } } // If the element is not found, return if (index == -1) { return; } // Replace the element to be deleted with the last element heap[index] = heap[heap.length - 1]; // Remove the last element heap.pop(); // Heapify the tree starting from the element at the deleted index while (true) { let left_child = 2 * index + 1; let right_child = 2 * index + 2; let smallest = index; if (left_child < heap.length && heap[left_child] < heap[smallest]) { smallest = left_child; } if (right_child < heap.length && heap[right_child] < heap[smallest]) { smallest = right_child; } if (smallest != index) { [heap[index], heap[smallest]] = [heap[smallest], heap[index]]; index = smallest; } else { break; } } } // Main function to test the insertMinHeap and deleteMinHeap functions let heap = []; let values = [13, 16, 31, 41, 51, 100]; for (let i = 0; i < values.length; i++) { insertMinHeap(heap, values[i]); } console.log('Initial heap: ' + heap.join(' ')); deleteMinHeap(heap, 13); console.log('Heap after deleting 13: ' + heap.join(' '));> Výkon
Initial heap: 13 16 31 41 51 100 Heap after deleting 13: 16 41 31 100 51>
Časová zložitosť : O(log n), kde n je číslo prvkov v halde
Pomocný priestor: O(n)
3. Operácia náhľadu na dátovej štruktúre Min-Heap:
Na prístup k minimálnemu prvku (t. j. ku koreňu haldy) sa vráti hodnota koreňového uzla. Časová zložitosť náhľadu v min-hromade je O(1).
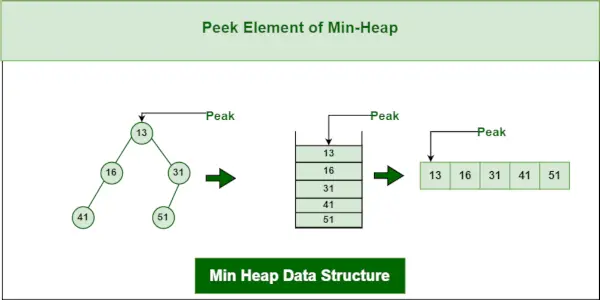
Štruktúra údajov minimálnej haldy
Implementácia operácie Peek v Min-Heap:
C++ #include #include #include using namespace std; int main() { // Create a max heap with some elements using a // priority_queue priority_queue , väčší > minHeap; minHeap.push(9); minHeap.push(8); minHeap.push(7); minHeap.push(6); minHeap.push(5); minHeap.push(4); minHeap.push(3); minHeap.push(2); minHeap.push(1); // Získanie vrcholového prvku (t. j. najväčšieho prvku) int peakElement = minHeap.top(); // Vytlačí vrcholový prvok cout<< 'Peak element: ' << peakElement << std::endl; return 0; }> Java import java.util.PriorityQueue; public class GFG { public static void main(String[] args) { // Create a max heap with some elements using a // PriorityQueue PriorityQueue minHeap = new PriorityQueue (); minHeap.add(9); minHeap.add(8); minHeap.add(7); minHeap.add(6); minHeap.add(5); minHeap.add(4); minHeap.add(3); minHeap.add(2); minHeap.add(1); // Získanie vrcholového prvku (t. j. najväčšieho prvku) int peakElement = minHeap.peek(); // Vytlačí vrcholový prvok System.out.println('Prvok vrcholu: ' + peakElement); } }> Python3 import heapq # Create a min heap with some elements using a list min_heap = [9, 8, 7, 6, 5, 4, 3, 2, 1] heapq.heapify(min_heap) # Get the peak element (i.e., the smallest element) peak_element = heapq.nsmallest(1, min_heap)[0] # Print the peak element print('Peak element:', peak_element)> C# using System; using System.Collections.Generic; public class GFG { public static void Main() { // Create a min heap with some elements using a // PriorityQueue var minHeap = new PriorityQueue (); minHeap.Enqueue(9); minHeap.Enqueue(8); minHeap.Enqueue(7); minHeap.Enqueue(6); minHeap.Enqueue(5); minHeap.Enqueue(4); minHeap.Enqueue(3); minHeap.Enqueue(2); minHeap.Enqueue(1); // Získanie vrcholového prvku (t. j. najmenšieho prvku) int peakElement = minHeap.Peek(); // Vytlačí prvok vrcholu Console.WriteLine('Prvok vrcholu: ' + peakElement); } }> Javascript const PriorityQueue = require('fast-priority-queue'); // Create a min heap with some elements using a PriorityQueue const minHeap = new PriorityQueue((a, b) =>a - b); minHeap.add(9); minHeap.add(8); minHeap.add(7); minHeap.add(6); minHeap.add(5); minHeap.add(4); minHeap.add(3); minHeap.add(2); minHeap.add(1); // Získame vrcholový prvok (t. j. najmenší prvok) const peakElement = minHeap.peek(); // Vytlačí prvok vrcholu console.log(`Prvok vrcholu: ${peakElement}`);> Výkon
Peak element: 1>
Časová zložitosť : V minimálnej halde implementovanej pomocou poľa alebo zoznamu môže byť vrcholový prvok prístupný v konštantnom čase, O(1), pretože je vždy umiestnený v koreňovom adresári haldy.
V min halde implementovanej pomocou binárneho stromu môže byť vrcholový prvok prístupný aj v čase O(1), pretože sa vždy nachádza v koreni stromu.
Pomocný priestor: O(n)
4. Operácia heapify na dátovej štruktúre Min-Heap:
Operáciu heapify možno použiť na vytvorenie minimálnej haldy z nezoradeného poľa. To sa dosiahne tak, že sa začne v poslednom nelistovom uzle a opakovane sa vykoná operácia bubliny, kým všetky uzly nesplnia vlastnosť haldy.
Operácia Heapify v Min Heap
Implementácia operácie Heapify v Min-Heap:
C++ #include #include using namespace std; void minHeapify(vector &arr, int i, int n) { int najmenší = i; int 1 = 2*i + 1; int r = 2*i + 2; ak (l< n && arr[l] < arr[smallest]) smallest = l; if (r < n && arr[r] < arr[smallest]) smallest = r; if (smallest != i) { swap(arr[i], arr[smallest]); minHeapify(arr, smallest, n); } } int main() { vector arr = {10, 5, 15, 2, 20, 30}; cout<< 'Original array: '; for (int i = 0; i < arr.size(); i++) cout << arr[i] << ' '; // Perform heapify operation on min-heap for (int i = arr.size()/2 - 1; i>= 0; i--) minHeapify(arr, i, arr.size()); cout<< '
Min-Heap after heapify operation: '; for (int i = 0; i < arr.size(); i++) cout << arr[i] << ' '; return 0; }>
Java // Java code of Heapify operation in Min-Heap import java.util.Arrays; import java.util.List; public class Main { // Function to maintain the min-heap property of the heap rooted at index 'i' public static void minHeapify(List arr, int i, int n) { // Predpokladajme, že koreň je najmenší prvok pôvodne int najmenší = i; // Vypočítajte indexy ľavého a pravého potomka aktuálneho uzla int l = 2 * i + 1; int r = 2 * i + 2; // Porovnajte ľavé dieťa so súčasným najmenším if (l< n && arr.get(l) < arr.get(smallest)) smallest = l; // Compare the right child with the current smallest if (r < n && arr.get(r) < arr.get(smallest)) smallest = r; // If the current node is not the smallest, swap it with the smallest child if (smallest != i) { int temp = arr.get(i); arr.set(i, arr.get(smallest)); arr.set(smallest, temp); // Recursively heapify the subtree rooted at the smallest child minHeapify(arr, smallest, n); } } public static void main(String[] args) { // Create a list representing the array List arr = Arrays.asList(10, 5, 15, 2, 20, 30); System.out.print('Pôvodné pole: '); // Vytlačí pôvodné pole pre (int i = 0; i< arr.size(); i++) System.out.print(arr.get(i) + ' '); // Perform heapify operation on the min-heap // Start from the last non-leaf node and go up to the root of the tree for (int i = arr.size() / 2 - 1; i>= 0; i--) minHeapify(arr, i, arr.size()); System.out.print('
Minálna halda po operácii heapify: '); // Vytlačí minimálnu haldu po operácii heapify pre (int i = 0; i< arr.size(); i++) System.out.print(arr.get(i) + ' '); } }> Python def minHeapify(arr, i, n): smallest = i left = 2 * i + 1 right = 2 * i + 2 if left < n and arr[left] < arr[smallest]: smallest = left if right < n and arr[right] < arr[smallest]: smallest = right if smallest != i: arr[i], arr[smallest] = arr[smallest], arr[i] minHeapify(arr, smallest, n) if __name__ == '__main__': arr = [10, 5, 15, 2, 20, 30] print('Original array:', arr) # Perform heapify operation on a min-heap for i in range(len(arr) // 2 - 1, -1, -1): minHeapify(arr, i, len(arr)) print('Min-Heap after heapify operation:', arr)> C# using System; using System.Collections.Generic; class GFG { // Function to perform the minHeapify operation on a min-heap. static void MinHeapify(List arr, int i, int n) { int najmenší = i; int left = 2 * i + 1; int vpravo = 2 * i + 2; // Porovnajte ľavé dieťa s aktuálnym najmenším uzlom. ak (vľavo< n && arr[left] < arr[smallest]) smallest = left; // Compare the right child with the current smallest node. if (right < n && arr[right] < arr[smallest]) smallest = right; // If the current node is not the smallest // swap it with the smallest child. if (smallest != i) { int temp = arr[i]; arr[i] = arr[smallest]; arr[smallest] = temp; // Recursively call minHeapify on the affected subtree. MinHeapify(arr, smallest, n); } } static void Main(string[] args) { List arr = nový zoznam { 10, 5, 15, 2, 20, 30}; Console.Write('Pôvodné pole: '); foreach (int num in arr) Console.Write(num + ' '); // Vykonajte operáciu heapify na min-halde. for (int i = arr.Count / 2 - 1; i>= 0; i--) MinHeapify(arr, i, arr.Count); Console.Write('
Min-Heap po operácii heapify: '); foreach (int num in arr) Console.Write(num + ' '); } }> Javascript // Define a function to perform min-heapify operation on an array function minHeapify(arr, i, n) { let smallest = i; let l = 2 * i + 1; let r = 2 * i + 2; // Check if left child is smaller than the current smallest element if (l < n && arr[l] < arr[smallest]) smallest = l; // Check if right child is smaller than the current smallest element if (r < n && arr[r] < arr[smallest]) smallest = r; // If the smallest element is not the current element, swap them if (smallest !== i) { [arr[i], arr[smallest]] = [arr[smallest], arr[i]]; minHeapify(arr, smallest, n); } } // Main function function main() { const arr = [10, 5, 15, 2, 20, 30]; // Print the original array console.log('Original array: ' + arr.join(' ')); // Perform heapify operation on the min-heap for (let i = Math.floor(arr.length / 2) - 1; i>= 0; i--) minHeapify(arr, i, arr.length); // Vytlačí minimálnu haldu po operácii heapify console.log('Min-Heap po operácii heapify: ' + arr.join(' ')); } // Volanie funkcie main na spustenie procesu main();> Výkon
Original array: 10 5 15 2 20 30 Min-Heap after heapify operation: 2 5 15 10 20 30>
Časová zložitosť heapify v min-hromade je O(n).
5. Operácia vyhľadávania na dátovej štruktúre Min-Heap:
Ak chcete vyhľadať prvok v minimálnej halde, možno vykonať lineárne vyhľadávanie v poli, ktoré predstavuje haldu. Časová zložitosť lineárneho vyhľadávania je však O(n), čo nie je efektívne. Preto vyhľadávanie nie je bežne používaná operácia v minimálnom množstve.
int parseint
Tu je príklad kódu, ktorý ukazuje, ako hľadať prvok v minimálnom množstve pomocou std::find() :
C++ #include using namespace std; int main() { priority_queue , väčší > min_heap; // príklad max haldy min_heap.push(10); min_heap.push(9); min_heap.push(8); min_heap.push(6); min_heap.push(4); prvok int = 6; // nájdený prvok na vyhľadanie bool = false; // Skopírujte minimálnu haldu do dočasného frontu a vyhľadajte // prvok std::priority_queue , väčší > teplota = min_hromada; while (!temp.empty()) { if (temp.top() == prvok) { found = true; prestávka; } temp.pop(); } if (nájdené) { std::cout<< 'Element found in the min heap.' << std::endl; } else { std::cout << 'Element not found in the min heap.' << std::endl; } return 0; }> Java import java.util.PriorityQueue; public class GFG { public static void main(String[] args) { PriorityQueue min_heap = new PriorityQueue (); min_heap.add( 3); // vloženie prvkov do prioritného frontu min_heap.offer(1); min_hromada.ponuka(4); min_hromada.ponuka(1); min_hromada.ponuka(6); prvok int = 6; // nájdený prvok na hľadanie booleov = false; // Skopírujte minimálnu haldu do dočasného frontu a vyhľadajte // prvok PriorityQueue temp = new PriorityQueue(min_heap); while (!temp.isEmpty()) { if (temp.poll() == prvok) { found = true; prestávka; } } if (nájdené) { System.out.println( 'Prvok nájdený v min. halde.'); } else { System.out.println( 'Prvok sa nenašiel v min. halde.'); } } }> Python3 import heapq min_heap = [1, 2, 3, 5, 6, 7, 8, 10] # example min heap heapq.heapify(min_heap) element = 6 # element to search for found = False # Copy the min heap to a temporary list and search for the element temp = list(min_heap) while temp: if heapq.heappop(temp) == element: found = True break if found: print('Element found in the min heap.') else: print('Element not found in the min heap.')> C# using System; using System.Collections.Generic; public class GFG { public static void Main() { var minHeap = new PriorityQueue (); // príklad min haldy minHeap.Enqueue(4); minHeap.Enqueue(6); minHeap.Enqueue(8); minHeap.Enqueue(9); minHeap.Enqueue(10); prvok int = 6; // nájdený prvok na vyhľadanie bool = false; // Skopírujte minimálnu haldu do dočasného frontu a vyhľadajte // prvok var temp = new PriorityQueue (minHeap); while (temp.Count> 0) { if (temp.Peek() == prvok) { found = true; prestávka; } temp.Dequeue(); } if (nájdené) { Console.WriteLine( 'Prvok nájdený v min. halde.'); } else { Console.WriteLine( 'Prvok sa nenašiel v min. halde.'); } } }> Javascript // Example min heap let minHeap = new PriorityQueue(); minHeap.enqueue(4); minHeap.enqueue(6); minHeap.enqueue(8); minHeap.enqueue(9); minHeap.enqueue(10); let element = 6; // Element to search for let found = false; // Copy the min heap to a temporary queue and search for the element let temp = new PriorityQueue(minHeap); while (temp.size()>0) { if (temp.peek() == prvok) { found = true; prestávka; } temp.dequeue(); } if (nájdené) { console.log('Prvok nájdený v min. halde.'); } else { console.log('Prvok sa nenašiel v min. halde.'); }> Výkon
Element found in the min heap.>
Analýza zložitosti :
The časová zložitosť tohto programu je O(n log n) , kde n je počet prvkov v prioritnom fronte.
Operácia vkladania má časovú zložitosť O (log n) v najhoršom prípade, pretože je potrebné udržiavať vlastnosť haldy. Operácia vyhľadávania zahŕňa skopírovanie prioritného frontu do dočasného frontu a následné prechádzanie dočasným frontom, čo trvá O(n log n) čas v najhoršom prípade, pretože každý prvok je potrebné skopírovať a vybrať z frontu a prioritný front sa musí pre každú operáciu prebudovať.
The priestorovú zložitosť programu je O(n) pretože ukladá n prvkov v prioritnom fronte a vytvorí dočasný front s n prvkov.
Aplikácie dátovej štruktúry Min-Heap:
- Zoradenie haldy: Min halda sa používa ako kľúčový komponent v algoritme triedenia haldy, čo je efektívny triediaci algoritmus s časovou zložitosťou O(nlogn).
- Prioritný front: Prioritný front je možné implementovať pomocou minimálnej haldy údajovej štruktúry, kde prvok s minimálnou hodnotou je vždy v koreňovom adresári.
- Dijkstrov algoritmus: V Dijkstrovom algoritme sa minimálna halda používa na uloženie vrcholov grafu s minimálnou vzdialenosťou od počiatočného vrcholu. Vrchol s minimálnou vzdialenosťou je vždy v koreni haldy.
- Huffmanovo kódovanie: V Huffmanovom kódovaní sa minimálna hromada používa na implementáciu prioritného frontu na vytvorenie optimálneho prefixového kódu pre danú množinu znakov.
- Zlúčiť K zoradené polia: Vzhľadom na K triedené polia ich môžeme efektívne zlúčiť do jedného triedeného poľa pomocou minimálnej haldy dátovej štruktúry.
Výhody štruktúry údajov s minimálnou haldou:
- Efektívne vkladanie a mazanie : Min halda umožňuje rýchle vkladanie a mazanie prvkov s časovou zložitosťou O(log n), kde n je počet prvkov v halde.
- Efektívne vyhľadávanie minimálneho prvku: Minimálny prvok v min halde je vždy v koreňovom adresári haldy, ktorý je možné získať v čase O(1).
- Priestorovo efektívne: Min halda je kompaktná dátová štruktúra, ktorú možno implementovať pomocou poľa alebo binárneho stromu, vďaka čomu je priestorovo efektívna.
- Triedenie: Minimálna halda sa môže použiť na implementáciu efektívneho triediaceho algoritmu, ako je triedenie haldy s časovou zložitosťou O(n log n).
- Prioritný front: Minimálna halda sa môže použiť na implementáciu prioritného frontu, kde prvok s minimálnou prioritou možno efektívne získať v čase O(1).
- Všestrannosť: Min halda má niekoľko aplikácií v informatike, vrátane grafových algoritmov, kompresie dát a databázových systémov.
Celkovo je min halda užitočná a všestranná dátová štruktúra, ktorá ponúka efektívne operácie, priestorovú efektivitu a má niekoľko aplikácií v informatike.