Problémy regresie a pravdepodobnostnej klasifikácie možno vyriešiť pomocou Gaussovho procesu (GP), techniky učenia pod dohľadom. Pretože každý Gaussov proces možno považovať za nekonečne-dimenzionálne zovšeobecnenie mnohorozmernosti Gaussove rozdelenia , v názve sa objavuje výraz Gaussian. V tomto príspevku budeme diskutovať o Gaussových procesoch pre regresiu, ktoré sa tiež označujú ako regresia Gaussových procesov (GPR). Pomocou GPR bolo vyriešených množstvo skutočných problémov v oblasti vedy o materiáloch, chémie, fyziky a biológie.
Obsah
- Gaussova regresia procesu (GPR)
- Kľúčové pojmy Gaussovej regresie procesov (GPR)
- Matematická koncepcia Gaussovej regresie procesov (GPR)
- Implementácia Gaussovho procesu v Pythone
Gaussova regresia procesu (GPR)
Gaussova procesná regresia (GPR) je výkonná a flexibilná neparametrická regresná technika používaná v strojové učenie a štatistiky . Je to užitočné najmä pri riešení problémov so spojitými údajmi, kde vzťah medzi vstupnými premennými a výstupom nie je explicitne známy alebo môže byť zložitý. GPR je bayesovský prístup, ktorý dokáže modelovať istotu v predpovediach, vďaka čomu je cenným nástrojom pre rôzne aplikácie vrátane optimalizácie, predpovedí časových radov a ďalších. GPR je založená na koncepte Gaussovho procesu, čo je súbor náhodných premenných, ktorých ľubovoľný konečný počet má spoločné Gaussovo rozdelenie. Gaussov proces si možno predstaviť ako rozdelenie funkcií.
Kľúčové pojmy Gaussovej regresie procesov (GPR)
Gaussainov proces
Neparametrický, pravdepodobnostný model nazývaný a Gaussov proces (GP) sa používa v štatistike a strojovom učení na regresiu, klasifikáciu a kvantifikáciu neistoty. Zobrazuje skupinu náhodných premenných, z ktorých každá má spoločné Gaussovo rozdelenie a môže mať konečný počet. Praktickí lekári sú všestrannou a efektívnou technikou na modelovanie zložitých vzťahov v údajoch a vytváranie predpovedí so súvisiacou neistotou.
Charakteristika Gaussových procesov :
- Neparametrická povaha : Praktickí lekári sa môžu prispôsobiť zložitosti údajov, pretože sa nespoliehajú na stanovený počet parametrov modelu
- Pravdepodobnostné predpovede : Predpovede od všeobecných lekárov možno kvantifikovať, pretože poskytujú predpovede ako rozdelenia pravdepodobnosti.
- Interpolácia a vyhladzovanie : GP sú užitočné pre zašumené alebo nepravidelne vzorkované údaje, pretože sú dobré pri vyhladzovaní zašumených údajov a interpolácii medzi údajovými bodmi.
- Marginalizácia hyperparametrov : Odstránením požiadavky na explicitné ladenie hyperparametrov marginalizujú hyperparametre, čím sa model zjednoduší.
Priemerná funkcia
Predpovedaná hodnota funkcie, ktorá sa modeluje v každom vstupnom bode, je reprezentovaná stredná funkcia v Gaussových procesoch (GP). Funguje ako základný predpoklad týkajúci sa základnej štruktúry údajov. Stredná funkcia je často predvolene nastavená na nulu, nie nevyhnutne a možno ju upraviť na základe vlastností údajov alebo odbornosti domény. Ovplyvnením centrálnej tendencie prognóz pomáha všeobecným lekárom identifikovať vzory alebo trendy v údajoch. Praktickí lekári poskytujú pravdepodobnostné predpovede, ktoré obsahujú neistotu, ako aj bodové odhady zahrnutím strednej funkcie
Funkcia kovariancie (jadra).
The kovariančná funkcia , tiež označovaná ako funkcia jadra, meria, nakoľko sú si navzájom podobné vstupné dátové body v Gaussových procesoch (GP). Je to nevyhnutné pri charakterizácii správania modelu GP, ovplyvňujúceho výber funkcií z predchádzajúcej distribúcie. Kovariančná funkcia meria párové podobnosti, aby sa zistila korelácia medzi funkčnými hodnotami. GP sa môžu prispôsobiť širokému spektru dátových vzorov, od hladkých trendov až po zložité štruktúry, pretože rôzne funkcie jadra zachytávajú rôzne druhy korelácií. Výkon modelu môže byť výrazne ovplyvnený výberom jadra.
Predchádzajúce distribúcie
The predchádzajúcej distribúcie , v Gaussových procesoch (GP), je naše chápanie funkcií pred pozorovaním akýchkoľvek údajov. Zvyčajne je opísaná kovariančnou (kernelovou) funkciou a strednou funkciou. Zatiaľ čo kovariančná funkcia opisuje podobnosť alebo koreláciu medzi funkčnými hodnotami v rôznych vstupných bodoch, stredná funkcia kóduje naše predchádzajúce očakávania. Toto vopred používajú praktickí lekári na vytvorenie distribúcie funkcií. V praktických lekároch je možné vybrať priority tak, aby predstavovali neistotu údajov, integrovali znalosti domény alebo indikovali hladkosť.
Zadné distribúcie
Gaussove procesy neskoršia distribúcia ukazuje naše revidované predpoklady o funkciách po pozorovaní údajov. Dá dohromady pravdepodobnosť údajov danej funkciou a predchádzajúcou distribúciou. Posterior v regresii GP ponúka rozdelenie funkcií, ktoré sa najviac zhodujú s pozorovanými údajmi. Tým, že umožňuje pravdepodobnostné predpovede a kvantifikáciu neistoty, zadné rozdelenie odráža kompromis medzi predchádzajúcimi presvedčeniami uloženými v predchádzajúcom rozdelení a informáciami poskytnutými údajmi.
Matematická koncepcia Gaussovej regresie procesov (GPR)
Pre regresné úlohy sa používa neparametrický, pravdepodobnostný model strojového učenia nazývaný regresia Gaussovho procesu (GP). Pri modelovaní zložitých a nejednoznačných interakcií medzi vstupnými a výstupnými premennými je to účinný nástroj. Predpokladá sa, že viacrozmerná Gaussova distribúcia vytvára dátové body v GP regresii a cieľom je odvodiť túto distribúciu.
GP regresný model má nasledujúce matematické vyjadrenie. Predpokladajme x1, X2,…..,Xnsú vstupné dátové body, kde x patrí reálnym číslam (-2,-1,0,1…), (xi
Predpokladajme, že y1, a2,……., ansú výstupné hodnoty, kde yipatrí reálnemu číslu (yi
GP regresný model vychádza z predpokladu, že Gaussov proces so strednou funkciou (
Potom v súbore testovacích miest x* je rozdelenie f dané:
Typicky sa funkcie jadra používajú na definovanie strednej funkcie a kovariančnej funkcie. Pre ilustráciu, štvorcové exponenciálne jadro, ktoré sa často používa, je opísané ako:
Kde,
k(x_{i}, x_{j}) = Funkcia jadra je reprezentovaná týmto a vypočítava koreláciu alebo podobnosť medzi dvoma vstupnými dátovými bodmi, xia xj.sigma^2 = Parameter rozptylu jadra je toto. Stanovuje rozsah alebo vertikálne rozšírenie funkcie jadra. Reguluje, ako silne sú dátové body korelované. Vyššiesigma^2 poskytuje funkciu jadra s väčším rozptylom.- exp: Exponenciálna funkcia je zodpovedná za zvýšenie e na mocninu argumentu.
||x_{i} – x_{j}||^2 : Rozdiel medzi vstupnými dátovými bodmi, xia xj, je druhá mocnina euklidovskej vzdialenosti. Meria sa geometrické vzdialenosti medzi bodmi v priestore prvkov.- l2: Toto je znázornenie dĺžkovej stupnice alebo charakteristickej dĺžky jadra. Reguluje rýchlosť, akou sa funkcia jadra zhoršuje, pretože dátové body sú od seba ďalej. Nižšie l spôsobí, že jadro bude degradovať rýchlejšie.
GP regresný model používa Bayesovu inferenciu na určenie distribúcie f, ktorá s najväčšou pravdepodobnosťou vytvorila údaje vzhľadom na súbor tréningových údajov (x, y). Aby sa to dosiahlo, musí sa vypočítať zadné rozdelenie f dané údajmi, ktoré je definované takto:
kde hraničná pravdepodobnosť údajov je p(y|x), predchádzajúce rozdelenie f je p(f) a pravdepodobnosť údajov danej funkciou f je (y|x,f).
Po naučení sa zadného rozdelenia f, model vypočíta zadné prediktívne rozloženie, aby urobil predpovede v ďalších testovacích bodoch x*. Dá sa definovať nasledovne:
Kde,
p(f^*|x*, y, x) = Toto ukazuje, vzhľadom na tréningové dáta y a x, podmienenú pravdepodobnosť predpovedaných funkčných hodnôt f*v novom vstupnom bode x*Inak povedané, je to rozdelenie pravdepodobnosti na všetky potenciálne funkčné hodnoty na novom vstupnom mieste x*, podmienené pozorovanými údajmi y a ich zodpovedajúcimi vstupnými miestami x.int p(f^*|x^*, f)p(f|y,x)df = V tejto časti rovnice sa na určenie podmienenej pravdepodobnosti používa integrál. Integrál zahŕňa všetky potenciálne hodnoty funkcie f.p(f^*|x^*, f) = Toto je podmienené rozdelenie pravdepodobnosti očakávaných funkčných hodnôt f*pri x*vzhľadom na funkčné hodnoty f na niektorých medziľahlých miestach.p(f|y,x) = Vzhľadom na pozorované údaje (y) a ich vstupné miesta (x) ide o podmienené rozdelenie pravdepodobnosti funkčných hodnôt (f).
Pre úlohy, ako je rozhodovanie s vedomím neistoty a aktívne učenie, táto distribúcia ponúka mieru neistoty predikcie, ktorá môže byť užitočná.
Kroky v Gaussovej regresii procesu
- Zber dát : Zhromaždite páry vstupno-výstupných údajov pre váš regresný problém.
- Vyberte funkciu jadra : Vyberte vhodnú kovariančnú funkciu (kernel), ktorá vyhovuje vášmu problému. Výber jadra ovplyvňuje tvar funkcií, ktoré môže GPR modelovať.
- Optimalizácia parametrov : Odhadnite hyperparametre funkcie jadra maximalizáciou pravdepodobnosti údajov. Dá sa to dosiahnuť pomocou optimalizačných techník, ako je gradientný zostup.
- Predpoveď: Na základe nového vstupu použite natrénovaný model GPR na vytváranie predpovedí. GPR poskytuje predpovedaný priemer a súvisiacu neistotu (rozptyl).
Implementácia Gaussovej procesnej regresie (GPR)
Python import numpy as np import matplotlib.pyplot as plt from sklearn.gaussian_process import GaussianProcessRegressor from sklearn.gaussian_process.kernels import RBF from sklearn.model_selection import train_test_split # Generate sample data np.random.seed(0) X = np.sort(5 * np.random.rand(80, 1), axis=0) y = np.sin(X).ravel() # Add noise to the data y += 0.1 * np.random.randn(80) # Define the kernel (RBF kernel) kernel = 1.0 * RBF(length_scale=1.0) # Create a Gaussian Process Regressor with the defined kernel gp = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=10) # Split the data into training and testing sets X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.5, random_state=0) # Fit the Gaussian Process model to the training data gp.fit(X_train, y_train) # Make predictions on the test data y_pred, sigma = gp.predict(X_test, return_std=True) # Visualize the results x = np.linspace(0, 5, 1000)[:, np.newaxis] y_mean, y_cov = gp.predict(x, return_cov=True) plt.figure(figsize=(10, 5)) plt.scatter(X_train, y_train, c='r', label='Training Data') plt.plot(x, y_mean, 'k', lw=2, zorder=9, label='Predicted Mean') plt.fill_between(x[:, 0], y_mean - 1.96 * np.sqrt(np.diag(y_cov)), y_mean + 1.96 * np.sqrt(np.diag(y_cov)), alpha=0.2, color='k', label='95% Confidence Interval') plt.xlabel('X') plt.ylabel('y') plt.legend() plt.show()> Výkon:
V tomto kóde najskôr vygenerujte niekoľko vzorových údajových bodov s pridaným šumom, potom definujte jadro RBF a vytvorte a Regresor Gaussovho procesu s tým. Model sa trénuje na trénovacích údajoch a používa sa na predpovede z testovacích údajov. Nakoniec sú výsledky vizualizované grafom zobrazujúcim tréningové dáta, predpokladaný priemer a 95% interval spoľahlivosti.
Implementácia Gaussovho procesu v Pythone
Scikit Learn
Python import matplotlib.pyplot as plt import numpy as np from scipy import linalg from sklearn.gaussian_process import kernels,GaussianProcessRegressor ## check version import sys import sklearn print(sys.version) !python --version print("numpy:", np.__version__) print("sklearn:",sklearn.__version__)> Pomocou tohto kódu sú importované potrebné knižnice pre Gaussovu procesnú regresiu (GPR) v Pythone; toto sú SciPy pre funkcie lineárnej algebry, NumPy pre numerické operácie a Matplotlib pre vizualizáciu dát. Aby sa uistil, že je kompatibilný s potrebnými balíkmi, dodatočne overí verziu Pythonu a vytlačí ju spolu s verziami NumPy a scikit-learn (sklearn).
Výber jadra
Python np.random.seed(0) n=50 kernel_ =[kernels.RBF (), kernels.RationalQuadratic(), kernels.ExpSineSquared(periodicity=10.0), kernels.DotProduct(sigma_0=1.0)**2, kernels.Matern() ] print(kernel_, '
')> Výkon:
[RBF(dĺžka_mierka=1),
RationalQuadratic(alpha=1, length_scale=1),
ExpSineSquared(dĺžka_mierka=1, periodicita=10),
DotProduct(sigma_0=1) ** 2,
Materská(dĺžka_mierka=1, nu=1,5)]
latexová veľkosť textu
Kód špecifikuje počet testovacích miest (n) a inicializuje a náhodné semeno . Aby sa zobrazili vybrané jadrá, vygeneruje zoznam niekoľkých funkcií jadra a vytlačí zoznam.
Porovnanie a vizualizácia jadra
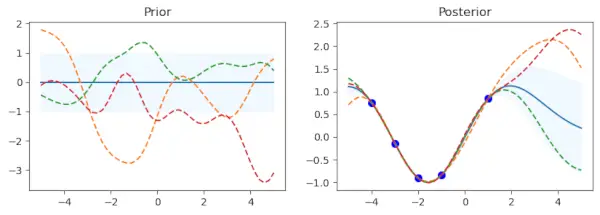
Python for kernel in kernel_: # Gaussian process gp = GaussianProcessRegressor(kernel=kernel) # Prior x_test = np.linspace(-5, 5, n).reshape(-1, 1) mu_prior, sd_prior = gp.predict(x_test, return_std=True) samples_prior = gp.sample_y(x_test, 3) # plot plt.figure(figsize=(10, 3)) plt.subplot(1, 2, 1) plt.plot(x_test, mu_prior) plt.fill_between(x_test.ravel(), mu_prior - sd_prior, mu_prior + sd_prior, color='aliceblue') plt.plot(x_test, samples_prior, '--') plt.title('Prior') # Fit x_train = np.array([-4, -3, -2, -1, 1]).reshape(-1, 1) y_train = np.sin(x_train) gp.fit(x_train, y_train) # posterior mu_post, sd_post = gp.predict(x_test, return_std=True) mu_post = mu_post.reshape(-1) samples_post = np.squeeze(gp.sample_y(x_test, 3)) # plot plt.subplot(1, 2, 2) plt.plot(x_test, mu_post) plt.fill_between(x_test.ravel(), mu_post - sd_post, mu_post + sd_post, color='aliceblue') plt.plot(x_test, samples_post, '--') plt.scatter(x_train, y_train, c='blue', s=50) plt.title('Posterior') plt.show() print("gp.kernel_", gp.kernel_) print("gp.log_marginal_likelihood:", gp.log_marginal_likelihood(gp.kernel_.theta)) print('-'*50, '
')> Výkon:
RBF
gp.kernel_ RBF(length_scale=1,93)
gp.log_marginal_likelihood: -3,444937833462133
-------------------------------------------------- -
Racionálna kvadratická

gp.kernel_ RationalQuadratic(alpha=1e+05, length_scale=1,93)
gp.log_marginal_likelihood: -3,4449718909150966
--------------------------------------------------
ExpSineSquared

gp.kernel_ ExpSineSquared(dĺžka_mierka=0,000524, periodicita=2,31e+04)
gp.log_marginal_likelihood: -3,4449381454930217
--------------------------------------------------
Skalárny súčin

gp.kernel_ DotProduct(sigma_0=0,998) ** 2
gp.log_marginal_likelihood: -150204291,56018084
--------------------------------------------------
Materská

gp.kernel_ Matern(length_scale=1,99, nu=1,5)
gp.log_marginal_likelihood: -5,131637070524745
--------------------------------------------------
Kód začína cyklovaním rôznych funkcií jadra uvedených v zozname kernel_ list. Gaussovský procesný regresor (gp) je vytvorený pomocou konkrétneho jadra pre každé jadro. Pre Gaussov proces to vytvára kovariančnú štruktúru. Na posúdenie predchádzajúcej distribúcie sa vytvorí sada testovacích vstupných bodov nazývaná x_test s hodnotami v rozsahu od -5 do 5. Táto sada bodov sa transformuje na stĺpcový vektor.
Pomocou metódy gp.predict sa v každom testovacom bode určí priemer predchádzajúceho rozdelenia (mu_prior) a štandardná odchýlka (sd_prior). Hodnoty štandardnej odchýlky sa vyžadujú pomocou voľby return_std=True. gp.sample_y (x_test, 3) sa používa na získanie troch funkčných vzoriek z predchádzajúcej distribúcie.
Prvý podgraf zobrazuje priemer predchádzajúceho rozdelenia so štandardnou odchýlkou reprezentovanou tieňovanou oblasťou. Vzorky sú superponované ako prerušované čiary, zatiaľ čo priemer je zobrazený ako plná čiara. Existuje podzápletka s názvom Prior. Existuje definovaná množina tréningových dátových bodov (x_train) a cieľových hodnôt (y_train), ktoré s nimi súvisia. Model Gaussovho procesu je prispôsobený pomocou týchto bodov (gp.fit(x_train, y_train)). Päť dátových bodov so zodpovedajúcimi sínusovými hodnotami tvorí tréningové dáta v tomto kóde.
Po fáze prispôsobenia tréningových údajov postup vypočíta strednú hodnotu zadnej distribúcie (mu_post) a štandardnú odchýlku (sd_post) pre rovnaké testovacie body (x_test). gp.sample_y(x_test, 3) sa tiež používa na vytváranie funkčných vzoriek zo zadnej distribúcie. Druhý podgraf prekrýva vzorkované funkcie ako bodkované čiary a ukazuje priemer zadnej distribúcie, tieňovaný so štandardnou odchýlkou. Modrou farbou sú vyznačené tréningové dátové body. Podzápletka má názov Posterior.
Ak chcete vidieť predchádzajúce a nasledujúce grafy pre aktuálne jadro a získať vizuálne pochopenie správania modelu, zavolajte plt.show() funkcie Matplotlib.
Kód zobrazuje podrobnosti o aktuálnom jadre, ako napríklad gp.kernel_, ktorý označuje aktuálne používané jadro a gp.log_marginal_likelihood (gp.kernel_.theta), ktorý udáva logaritmickú hraničnú pravdepodobnosť modelu s použitím aktuálneho jadra po každej sade predchádzajúcich a zadných grafov.
Výhody Gaussovej regresie procesov (GPR)
Gaussova regresia procesov (GPR) má množstvo výhod v rade aplikácií:
- GPR poskytuje pravdepodobnostný rámec pre regresiu, čo znamená, že poskytuje nielen bodové odhady, ale poskytuje aj odhady neistoty pre predpovede.
- Je vysoko flexibilný a dokáže zachytiť zložité vzťahy v dátach.
- GPR je možné prispôsobiť rôznym aplikáciám, vrátane predpovedania časových radov, optimalizácie a bayesovskej optimalizácie.
Výzvy Gaussovej regresie procesov (GPR)
- GPR môže byť výpočtovo nákladné pri práci s veľkými súbormi údajov, pretože je potrebná inverzia kovariančnej matice.
- Výber funkcie jadra a jeho hyperparametrov môže výrazne ovplyvniť výkon modelu.
Dobré príklady aplikácií GPR
- Predikcia ceny akcií: GPR je možné použiť na modelovanie a predpovedanie cien akcií s prihliadnutím na volatilitu a neistotu na finančných trhoch.
- Počítačové experimenty: GPR je užitočná pri optimalizácii zložitých simulácií modelovaním vzťahov medzi vstupmi a výstupmi a identifikáciou najvplyvnejších parametrov.
- Detekcia anomálií: GPR možno použiť na detekciu anomálií, kde identifikuje nezvyčajné vzory v údajoch časových radov zachytením normálneho rozloženia údajov.
Záver
Na záver, Gaussova procesná regresia je cenným nástrojom na analýzu a predikciu údajov v situáciách, kde je nevyhnutné pochopiť neistotu v predpovediach. Využitím pravdepodobnostného modelovania a funkcií jadra môže GPR poskytnúť presné a interpretovateľné výsledky. Pri implementácii GPR v praxi je však kľúčové zvážiť výpočtové náklady a potrebu odborného vstupu.
