Vzorce Sin Cos v trigonometrii: Trigonometria, ako už názov napovedá, je štúdium trojuholníkov. Je to dôležité odvetvie matematiky, ktoré študuje vzťah medzi dĺžkami strán a uhlami pravouhlého trojuholníka a tiež pomáha pri určovaní chýbajúcich dĺžok strán alebo uhlov trojuholníka. Existuje šesť trigonometrických pomerov alebo funkcií: sínus, kosínus, tangens, kosekans, sekans a kotangens, kde kosekans, sekans a kotangens sú recipročné funkcie ostatných troch funkcií, t. j. sínus, kosínus a tangens.
Trigonometrický pomer je definovaný ako pomer dĺžok strán pravouhlého trojuholníka. Trigonometria sa používa v rôznych oblastiach nášho každodenného života. Pomáha určiť výšku kopcov alebo budov. Používa sa aj v oblastiach ako kriminológia, stavebníctvo, fyzika, archeológia, inžinierstvo lodných motorov atď.
V tomto článku preskúmame všetky trigonometrické vzorce väčšinou sin a cos vzorce s ich príkladmi a zoznam všetkých vzorcov v trigonometrii.
Obsah
- Vzorce v trigonometrii
- Niektoré základné vzorce Sin Cos
- Tabuľka vzorcov Sin Cos
- Príklady vzorcov Sin Cos
- Cvičte problémy so vzorcami Sin Cos v trigonometrii s príkladmi
Vzorce v trigonometrii
Uvažujme pravouhlý trojuholník XYZ, kde ∠Y = 90°. Nech je uhol vo vrchole Z θ. Strana susediaca s θ sa nazýva susedná strana a strana opačná k θ sa nazýva opačná strana. Prepona je strana opačná k pravému uhlu alebo najdlhšia strana pravého uhla.
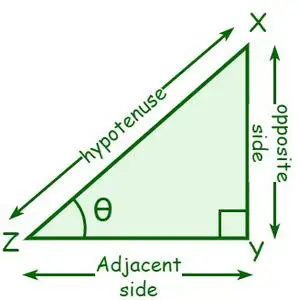
- sin θ = Opačná strana/hypotenúza
- cos θ = susediaca strana/hypotenúza
- tan θ = Opačná strana/Priľahlá strana
- cosec θ = 1/sin θ = prepona/opačná strana
- sek θ = 1/ cos θ = prepona/priľahlá strana
- detská postieľka θ = 1/ tan θ = Priľahlá strana/Opačná strana
Sínusový vzorec
Sínus uhla v pravouhlom trojuholníku je pomer dĺžky protiľahlej strany k dĺžke prepony k danému uhlu. Funkcia sínus je reprezentovaná ako sin.
sin θ = Opačná strana/hypotenúza
Kosínový vzorec
Kosínus uhla v pravouhlom trojuholníku je pomer dĺžky priľahlej strany k dĺžke prepony k danému uhlu. Kosínusová funkcia je reprezentovaná ako cos.
čo je mapa javacos θ = susediaca strana/hypotenúza
Niektoré základné vzorce Sin Cos
Sínusové a kosínusové funkcie v kvadrantoch
- Funkcia sínus je kladná v prvom a druhom kvadrante a záporná v treťom a štvrtom kvadrante.
- Kosínusová funkcia je kladná v prvom a štvrtom kvadrante a záporná v druhom a treťom kvadrante.
Stupne
Kvadrant
Funkcia Znak sínusu
Znak funkcie kosínus
0° až 90°
1. kvadrant
+ (kladné)
+ (kladné)
90° až 180°
2. kvadrant
+ (kladné)
– (negatívne)
180° až 270°
3. kvadrant
– (negatívne)
– (negatívne)
270° až 360°
4. kvadrant
– (negatívne)
+ (kladné)
Identita záporného uhla funkcií sínus a kosínus
- Sínus záporného uhla sa vždy rovná zápornému sínusu uhla.
sin (– θ) = – sin θ
- Kosínus záporného uhla sa vždy rovná kosínusu uhla.
cos (– θ) = cos θ
Vzťah medzi funkciou sínus a kosínus
sin θ = cos (90° – θ)
Recipročné funkcie funkcií sínus a kosínus
- Funkcia kosekans je recipročná funkcia funkcie sínus.
cosec θ = 1/sin θ
- Funkcia Secant je recipročná funkcia kosínusovej funkcie.
sek. 0 = 1/cos 9
Pytagorejská identita
bez 2 θ + cos 2 θ = 1
Periodické identity funkcií sínus a kosínus
sin (θ + 2nπ) = sin θ
cos (θ + 2nπ) = cos θ
Vzorce dvojitého uhla pre funkcie sínus a kosínus
sin 2θ = 2 sin θ cos θ
cos 2θ = cos 2 θ – hriech 2 θ = 2 cos 2 θ – 1 = 1 – 2 hriech 2 i
Polovičné uhly pre funkcie sínus a kosínus
sin (θ/2) = ±√[(1 – cos θ)/2]
cos (θ/2) = ±√[(1 + cos θ)/2]
Trojité uhly pre funkcie sínus a kosínus
sin 3θ = 3 sin θ – 4 sin 3 i
cos 3θ = 4cos 3 θ – 3 cos θ
Vzorce súčtu a rozdielu
- Funkcia sínus
sin (A + B) = sin A cos B + cos A sin B
hriech (A – B) = sin A cos B – cos A sin B
- Kosínusová funkcia
cos (A + B) = cos A cos B – hriech A hriech B
cos (A – B) = cos A cos B + sin A sin B
Sínusový zákon alebo sínusové pravidlo
Sínusový zákon je trigonometrický zákon, ktorý udáva vzťah medzi dĺžkami strán a uhlami trojuholníka.

a/sin A = b/sin B = c/sin C
Kde a, b a c sú dĺžky troch strán trojuholníka ABC a A, B a C sú uhly.
Zákon kosínusov
Zákon kosínusov kosínusového pravidla sa používa na určenie chýbajúcich alebo neznámych uhlov alebo dĺžok strán trojuholníka.

a 2 = b 2 + c 2 – 2 bc čos A
b 2 = c 2 + a 2 – 2 ca ako B
c 2 = a 2 + b 2 – 2ab čos C
Kde a, b a c sú dĺžky troch strán trojuholníka ABC a A, B a C sú uhly.
Tabuľka vzorcov Sin Cos
Tu je tabuľka/zoznam vzorcov Sin a Cos pre rôzne uhly v stupňoch a radiánoch:
Zoznam vzorcov Sin Cos
| Uhol (v stupňoch) | Uhol (v radiánoch) | hriech i | cos θ |
|---|---|---|---|
| 0° | 0 | 0 | 1 |
| 30° | p/6 | 1/2 | _3/2 |
| 45° | p/4 | 1/√2 | 1/√2 |
| 60° | p/3 | √3/2 | 1/2 |
| 90° | p/2 | 1 | 0 |
| 120° | 2p/3 | √3/2 | -1/2 |
| 150° | 5p/6 | 1/2 | -√3/2 |
| 180° | Pi | 0 | -1 |
Príklady vzorcov Sin Cos
Úloha 1: Ak cos α = 24/25, nájdite hodnotu sin α.
Riešenie:
Vzhľadom na to,
cos α = 24/25
Z pytagorovských identít, ktoré máme;
cos2θ + hriech2θ = 1
(24/25)2+ bez2a = 1
bez2α = 1 – (24/25)2
bez2α = 1 – (576/625) = (625 – 576)/625
bez2α = (625 – 576)/625 = 49/626
sin α = √49/625 = ±7/25
Preto sin α = ±7/25.
Úloha 2: Dokážte vzorce sin 2A a cos 2A, ak ∠A= 30°.
Riešenie:
Dané, ∠A= 30°
My to vieme,
1) sin 2A = 2 sin A cos A
sin 2(30°) = 2 sin 30° cos 30°
hriech 60° = 2 × (1/2) × (√3/2) {Od, hriech 30° = 1/2, cos 30° = √3/2 a hriech 60° = √3/2}
√3/2 = √3/2
L.H.S. = R.H.S
2) cos 2A = 2cos2A – 1
cos 2(30°) = 2cos2(30°) – 1
cos 60° = 2 (√3/2)2– 1 = 3/2 – 1 {Keďže cos 60° = 1/2 a cos 30° = √3/2}
1/2 = 1/2
L.H.S. = R.H.S
Preto dokázané.
Úloha 3: Nájdite hodnotu cos x, ak tan x = 3/4.
Riešenie:
Dané, tan x = 3/4
My to vieme,
tan x = opačná strana/susedná strana = 3/4
Na nájdenie prepony použijeme Pytagorovu vetu:
hypotenzia2= opak2+ susediace2
H2= 32+ 42
H2= 9 + 16 = 25
H = √25 = 5
Teraz, cos x = susedná strana/hypotenza
cos x = 4/5
Hodnota cos x je teda 4/5.
Úloha 4: Nájdite ∠C (v stupňoch) a ∠A (v stupňoch), ak ∠B = 45°, BC = 15 palcov a AC = 12 palcov.

Riešenie:
Dané: ∠B = 45°, BC = a = 15 palcov a AC = b = 12 palcov.
Zo zákona sínusov máme
a/sin A = b/sin B = c/sin C
⇒ a/sin A = b/sin B
⇒ 15/sin A = 12/sin 45°
⇒ 15/sin A = 12/(1/√2)
⇒ 15/sin A = 12√2 = 16,97
⇒ bez A = 15/16,97 = 0,8839
⇒ ∠A = hriech-1(0,8839) = 62,11°
Vieme, že súčet vnútorných uhlov trojuholníka je 180°.
Takže ∠A + ∠B + ∠C = 180°
⇒ 62,11° + 45° + ∠C = 180°
⇒ ∠C = 180° – (62,11° + 45°) = 72,89°
Preto ∠A = 62,11° a ∠C = 72,89°.
Úloha 5: Dokážte identitu polovičného uhla kosínusovej funkcie.
Riešenie:
Identita polovičného uhla kosínusovej funkcie je:
cos (θ/2) = ±√[(1 + cos θ)/2]
Z dvojitého uhla identít máme,
cos 2A = 2 cos2A – 1
Teraz vymeňte A za θ/2 na oboch stranách
⇒ cos 2(θ/2) = 2 cos2(i/2) – 1
⇒ cos θ = 2 cos2(i/2) – 1
⇒ 2cos2(0/2) = cos 9 + 1
⇒ cos2(0/2) = (cos 6 + 1)/2
⇒ cos (θ/2) = ±√[(1 + cos θ)/2]
reťazec na charPreto dokázané.
Cvičte problémy so vzorcami Sin Cos v trigonometrii s príkladmi
1. Daný sin θ = 3/5. Nájdite cos θ.
2. Dokážte identitu sin(2A) = 2 sinA cosA pre A=45∘.
3. Ak cos α = 5/13. Nájdite hriech (2a).
4. Vyriešte pre θ, ak sin θ = cos(90∘−θ).
5. Ak tan β = 2. Nájdite sin β a cos β pomocou Pytagorovej identity.
Časté otázky o vzorcoch Sin Cos v trigonometrii s príkladmi
Aké sú základné sínusové a kosínusové vzorce v trigonometrii?
Základné sínusové a kosínusové vzorce sú sin θ = Opačný/Hypotenúza a cos θ = Susedný/Hypotenúza, kde θ je uhol v pravouhlom trojuholníku.
Ako zistíte sínus a kosínus špeciálnych uhlov?
Špeciálne uhly ako 0°, 30°, 45°, 60° a 90° majú špecifické sínusové a kosínusové hodnoty, ktoré si možno zapamätať pomocou trigonometrických tabuliek alebo konceptov jednotkových kružníc.
Aký je vzťah medzi funkciami sínus a kosínus?
Funkcie sínus a kosínus sú spojené identitou sin θ = cos(90∘- θ) a pytagorejskej identity bez 2 θ+cos 2 θ = 1.
Ako používate vzorce dvojitého uhla pre sínus a kosínus?
Vzorce s dvojitým uhlom sú sin(2θ) = 2sinθcosθ a cos(20)=cos 2 θ – hriech 2 i. Používajú sa na vyjadrenie goniometrických funkcií dvojitých uhlov pomocou jednoduchých uhlov.
Ako zistíte hodnoty sínusu a kosínusu pre uhly v rôznych kvadrantoch?
Znaky funkcií sínus a kosínus závisia od kvadrantu, v ktorom leží uhol:
- Prvý kvadrant: sin θ> 0 a cos θ> 0
- Druhý kvadrant: sin θ> 0 a cos θ < 0
- Tretí kvadrant: sinθ <0 a cosθ < 0
- Štvrtý kvadrant: sinθ 0
