Ford-Fulkersonov algoritmus je široko používaný algoritmus na riešenie problému maximálneho toku v tokovej sieti. Problém maximálneho toku zahŕňa určenie maximálneho množstva toku, ktorý možno poslať zo zdrojového vrcholu do klesajúceho vrcholu v nasmerovanom váženom grafe, s výhradou kapacitných obmedzení na okrajoch.
Algoritmus funguje tak, že iteratívnym spôsobom hľadá rozširujúcu cestu, čo je cesta od zdroja k záchytu v zvyškovom grafe, t. j. graf získaný odčítaním toku prúdu od kapacity každej hrany. Algoritmus potom zvýši tok pozdĺž tejto dráhy o maximálne možné množstvo, čo je minimálna kapacita hrán pozdĺž dráhy.
problém:
Daný graf, ktorý predstavuje sieť tokov, kde každá hrana má kapacitu. Tiež vzhľadom na dva vrcholy zdroj „s“ a drez „t“ v grafe nájdite maximálny možný prietok od s do t s nasledujúcimi obmedzeniami:
- Prietok na hrane nepresahuje danú kapacitu hrany.
- Prichádzajúci tok sa rovná odchádzajúcemu toku pre každý vrchol okrem s a t.
Uvažujme napríklad o nasledujúcom grafe z knihy CLRS.
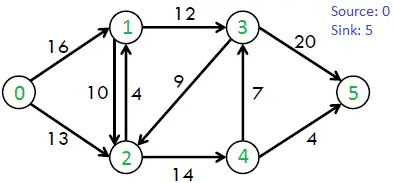
Maximálny možný prietok vo vyššie uvedenom grafe je 23.

Predpoklad: Úvod do problému maximálneho prietoku
Ford-Fulkersonov algoritmus
Nasleduje jednoduchá myšlienka Ford-Fulkersonovho algoritmu:
- Začnite s počiatočným tokom ako 0.
- Zatiaľ čo existuje rozširujúca cesta od zdroja k umývadlu:
- Nájdite rozširujúcu cestu pomocou ľubovoľného algoritmu hľadania cesty, ako je vyhľadávanie do šírky alebo do hĺbky.
- Určte množstvo toku, ktorý možno poslať pozdĺž zväčšujúcej cesty, čo je minimálna zvyšková kapacita pozdĺž okrajov cesty.
- Zvýšte prietok pozdĺž zväčšovacej dráhy o určené množstvo.
- Vráťte maximálny prietok.
Časová zložitosť: Časová zložitosť vyššie uvedeného algoritmu je O(max_flow * E). Spustíme slučku, kým existuje rozširujúca cesta. V najhoršom prípade môžeme pridať 1 tok jednotky v každej iterácii. Preto sa časová zložitosť stáva O(max_flow * E).
Ako implementovať vyššie uvedený jednoduchý algoritmus?
Najprv definujme koncept reziduálneho grafu, ktorý je potrebný na pochopenie implementácie.
Reziduálny graf prietokovej siete je graf, ktorý ukazuje ďalší možný prietok. Ak v reziduálnom grafe existuje cesta od zdroja k ponoru, potom je možné pridať prietok. Každá hrana zvyškového grafu má hodnotu tzv zvyšková kapacita čo sa rovná pôvodnej kapacite hrany mínus prietok prúdu. Zvyšková kapacita je v podstate aktuálna kapacita hrany.
arašidy vs arašidy
Poďme sa teraz porozprávať o detailoch implementácie. Zvyšková kapacita je 0, ak medzi dvoma vrcholmi zvyškového grafu nie je žiadna hrana. Môžeme inicializovať zvyškový graf ako pôvodný graf, pretože neexistuje žiadny počiatočný tok a počiatočná zvyšková kapacita sa rovná pôvodnej kapacite. Aby sme našli rozširujúcu cestu, môžeme buď urobiť BFS alebo DFS zvyškového grafu. Použili sme BFS v nižšie uvedenej implementácii. Pomocou BFS môžeme zistiť, či existuje cesta od zdroja k ponoru. BFS tiež vytvára nadradené[] pole. Pomocou poľa parent[] prechádzame cez nájdenú cestu a nájdeme možný prietok touto cestou nájdením minimálnej zvyškovej kapacity pozdĺž cesty. Neskôr pridáme tok nájdenej cesty k celkovému toku.
Dôležité je, že musíme aktualizovať zvyškové kapacity v grafe zvyškov. Odčítame tok cesty od všetkých hrán pozdĺž cesty a pridáme tok cesty pozdĺž reverzných hrán Potrebujeme pridať tok cesty pozdĺž reverzných hrán, pretože neskôr možno bude potrebné poslať tok v opačnom smere (pozri napríklad nasledujúci odkaz).
Nižšie je uvedená implementácia Ford-Fulkersonovho algoritmu. Aby to bolo jednoduché, graf je reprezentovaný ako 2D matica.
C++
linuxový hostiteľ
// C++ program for implementation of Ford Fulkerson> // algorithm> #include> #include> #include> #include> using> namespace> std;> // Number of vertices in given graph> #define V 6> /* Returns true if there is a path from source 's' to sink> >'t' in residual graph. Also fills parent[] to store the> >path */> bool> bfs(>int> rGraph[V][V],>int> s,>int> t,>int> parent[])> {> >// Create a visited array and mark all vertices as not> >// visited> >bool> visited[V];> >memset>(visited, 0,>sizeof>(visited));> >// Create a queue, enqueue source vertex and mark source> >// vertex as visited> >queue<>int>>q;> >q.push(s);> >visited[s] =>true>;> >parent[s] = -1;> >// Standard BFS Loop> >while> (!q.empty()) {> >int> u = q.front();> >q.pop();> >for> (>int> v = 0; v if (visited[v] == false && rGraph[u][v]>0) { // Ak nájdeme spojenie so sink uzlom, // potom už BFS nemá zmysel Musíme // len nastaviť jeho rodiča a môžeme vrátiť // true if (v == t) { parent[ v] = u; vrátiť true; } q.push(v); rodič[v] = u; navštívené[v] = pravda; } } } // Nedosiahli sme sink v BFS počnúc zdrojom, takže // vráti false return false; } // Vráti maximálny prietok od s do t v danom grafe int fordFulkerson(int graf[V][V], int s, int t) { int u, v; // Vytvorte zvyškový graf a vyplňte zvyškový graf // danými kapacitami v pôvodnom grafe ako // zvyškovými kapacitami v zvyškovom grafe int rGraph[V] [V]; // Zvyškový graf kde rGraph[i][j] // označuje zvyškovú kapacitu hrany // od i do j (ak existuje hrana. Ak // rGraph[i][j] je 0, tak nie je) for (u = 0; u for (v = 0; v rGraph[u][v] = graf[u][v]; int parent[V]; // Toto pole vyplní BFS a // uloží cestu int max_flow = 0 // Na začiatku nie je žiadny tok // Rozšírte tok, kým existuje cesta od zdroja k // klesnutiu while (bfs(rGraph, s, t, parent)) { // Nájdite minimálnu zvyškovú kapacitu hrán pozdĺž // cesty vyplnenej BFS Alebo môžeme povedať, že nájdeš // maximálny prietok cez nájdenú cestu int cesta_tok = INT_MAX pre (v = t; v != s; v = rodič[v]) { u = parent[v]; cesta_tok = min(cesta_tok, rGraf[u][v] } // aktualizácia zvyškových kapacít hrán a // obrátenie hrán pozdĺž cesty pre (v = t; v != s; v =); rodič[v]) { u = rodič[v]; rGraph[u][v] -= tok_cesty; // Vráti celkový tok return max_flow; } // Program ovládača na testovanie vyššie uvedených funkcií int main() { // Vytvorme graf zobrazený vo vyššie uvedenom príklade int graf[V][V] = { { 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 }, { 0, 4, 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 }, { 0, 0, 0, 7 , 0, 4}, { 0, 0, 0, 0, 0, 0}}; cout<< 'The maximum possible flow is ' << fordFulkerson(graph, 0, 5); return 0; }> |
>
>
Java
// Java program for implementation of Ford Fulkerson> // algorithm> import> java.io.*;> import> java.lang.*;> import> java.util.*;> import> java.util.LinkedList;> class> MaxFlow {> >static> final> int> V =>6>;>// Number of vertices in graph> >/* Returns true if there is a path from source 's' to> >sink 't' in residual graph. Also fills parent[] to> >store the path */> >boolean> bfs(>int> rGraph[][],>int> s,>int> t,>int> parent[])> >{> >// Create a visited array and mark all vertices as> >// not visited> >boolean> visited[] =>new> boolean>[V];> >for> (>int> i =>0>; i visited[i] = false; // Create a queue, enqueue source vertex and mark // source vertex as visited LinkedList queue = new LinkedList(); queue.add(s); visited[s] = true; parent[s] = -1; // Standard BFS Loop while (queue.size() != 0) { int u = queue.poll(); for (int v = 0; v if (visited[v] == false && rGraph[u][v]>0) { // Ak nájdeme spojenie so sink // uzlom, potom v BFS už nemá zmysel // Len musíme nastaviť jeho rodiča // a môžeme vrátiť true if (v == t) { parent[ v] = u; vrátiť true; } queue.add(v); rodič[v] = u; navštívené[v] = pravda; } } } // Nedosiahli sme klesnutie v BFS počnúc zdrojom, // takže return false return false; } // Vráti maximálny prietok od s do t v danom // grafe int fordFulkerson(int graf[][], int s, int t) { int u, v; // Vytvorte zvyškový graf a vyplňte zvyškový // graf danými kapacitami v pôvodnom grafe // ako zvyškové kapacity v grafe zvyškov // Zvyškový graf kde rGraph[i][j] označuje // zvyškovú kapacitu hrany od i do j (ak je tam // hrana. Ak rGraph[i][j] je 0, tak tam // nie je) int rGraph[][] = new int[V][V]; for (u = 0; u for (v = 0; v rGraph[u][v] = graf[u][v]; // Toto pole je vyplnené BFS a na uloženie cesty int parent[] = new int[ V] int max_flow = 0 // Na začiatku nie je žiadny tok // Rozšírte tok, kým existuje cesta zo zdroja // do klesania while (bfs(rGraph, s, t, rodič)) { // Nájdite minimálnu zvyškovú kapacitu; hrán // po ceste vyplnenej BFS Alebo môžeme povedať // nájsť maximálny prietok cez nájdenú cestu int cesta_tok = Integer.MAX_VALUE for (v = t; v != s; v = parent[v ]) { u = parent[v]; cesta_tok = Math.min(cesta_tok, rGraf[u][v] } // aktualizácia zvyškových kapacít hrán a // obrátenie hrán pozdĺž cesty pre (v = t; v != s; v = rodič[v]) { u = rodič[v]; rGraph[u][v] -= tok_cesty[v][u] += tok_cesty } // Pridanie toku cesty do celkovej; flow max_flow += cesta_tok } // Vráti celkový tok návrat max_flow } // Program ovládača na testovanie vyššie uvedených funkcií public static void main(String[] args) throws java.lang.Exception { // Vytvorme zobrazený graf; vo vyššie uvedenom príklade int graf[][] = new int[][] { { 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 }, { 0, 4 , 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 }, { 0, 0, 0, 7, 0, 4 }, { 0, 0, 0, 0, 0, 0 } }; MaxFlow m = new MaxFlow(); System.out.println('Maximálny možný prietok je ' + m.fordFulkerson(graf, 0, 5)); } }> |
>
algoritmus triedenia vloženia
>
Python
# Python program for implementation> # of Ford Fulkerson algorithm> from> collections>import> defaultdict> # This class represents a directed graph> # using adjacency matrix representation> class> Graph:> >def> __init__(>self>, graph):> >self>.graph>=> graph># residual graph> >self>. ROW>=> len>(graph)> ># self.COL = len(gr[0])> >'''Returns true if there is a path from source 's' to sink 't' in> >residual graph. Also fills parent[] to store the path '''> >def> BFS(>self>, s, t, parent):> ># Mark all the vertices as not visited> >visited>=> [>False>]>*>(>self>.ROW)> ># Create a queue for BFS> >queue>=> []> ># Mark the source node as visited and enqueue it> >queue.append(s)> >visited[s]>=> True> ># Standard BFS Loop> >while> queue:> ># Dequeue a vertex from queue and print it> >u>=> queue.pop(>0>)> ># Get all adjacent vertices of the dequeued vertex u> ># If a adjacent has not been visited, then mark it> ># visited and enqueue it> >for> ind, val>in> enumerate>(>self>.graph[u]):> >if> visited[ind]>=>=> False> and> val>>0>:> ># If we find a connection to the sink node,> ># then there is no point in BFS anymore> ># We just have to set its parent and can return true> >queue.append(ind)> >visited[ind]>=> True> >parent[ind]>=> u> >if> ind>=>=> t:> >return> True> ># We didn't reach sink in BFS starting> ># from source, so return false> >return> False> > > ># Returns the maximum flow from s to t in the given graph> >def> FordFulkerson(>self>, source, sink):> ># This array is filled by BFS and to store path> >parent>=> [>->1>]>*>(>self>.ROW)> >max_flow>=> 0> # There is no flow initially> ># Augment the flow while there is path from source to sink> >while> self>.BFS(source, sink, parent) :> ># Find minimum residual capacity of the edges along the> ># path filled by BFS. Or we can say find the maximum flow> ># through the path found.> >path_flow>=> float>(>'Inf'>)> >s>=> sink> >while>(s !>=> source):> >path_flow>=> min> (path_flow,>self>.graph[parent[s]][s])> >s>=> parent[s]> ># Add path flow to overall flow> >max_flow>+>=> path_flow> ># update residual capacities of the edges and reverse edges> ># along the path> >v>=> sink> >while>(v !>=> source):> >u>=> parent[v]> >self>.graph[u][v]>->=> path_flow> >self>.graph[v][u]>+>=> path_flow> >v>=> parent[v]> >return> max_flow> > # Create a graph given in the above diagram> graph>=> [[>0>,>16>,>13>,>0>,>0>,>0>],> >[>0>,>0>,>10>,>12>,>0>,>0>],> >[>0>,>4>,>0>,>0>,>14>,>0>],> >[>0>,>0>,>9>,>0>,>0>,>20>],> >[>0>,>0>,>0>,>7>,>0>,>4>],> >[>0>,>0>,>0>,>0>,>0>,>0>]]> g>=> Graph(graph)> source>=> 0>; sink>=> 5> > print> (>'The maximum possible flow is %d '> %> g.FordFulkerson(source, sink))> # This code is contributed by Neelam Yadav> |
>
>
C#
radenie java poľa
// C# program for implementation> // of Ford Fulkerson algorithm> using> System;> using> System.Collections.Generic;> public> class> MaxFlow {> >static> readonly> int> V = 6;>// Number of vertices in> >// graph> >/* Returns true if there is a path> >from source 's' to sink 't' in residual> >graph. Also fills parent[] to store the> >path */> >bool> bfs(>int>[, ] rGraph,>int> s,>int> t,>int>[] parent)> >{> >// Create a visited array and mark> >// all vertices as not visited> >bool>[] visited =>new> bool>[V];> >for> (>int> i = 0; i visited[i] = false; // Create a queue, enqueue source vertex and mark // source vertex as visited List |
>
>
Javascript
> // Javascript program for implementation of Ford> // Fulkerson algorithm> // Number of vertices in graph> let V = 6;> // Returns true if there is a path from source> // 's' to sink 't' in residual graph. Also> // fills parent[] to store the path> function> bfs(rGraph, s, t, parent)> {> > >// Create a visited array and mark all> >// vertices as not visited> >let visited =>new> Array(V);> >for>(let i = 0; i visited[i] = false; // Create a queue, enqueue source vertex // and mark source vertex as visited let queue = []; queue.push(s); visited[s] = true; parent[s] = -1; // Standard BFS Loop while (queue.length != 0) { let u = queue.shift(); for(let v = 0; v { if (visited[v] == false && rGraph[u][v]>0) { // Ak nájdeme spojenie so sink // uzlom, potom v BFS už nemá zmysel // Len musíme nastaviť jeho rodiča // a môžeme vrátiť true if (v == t) { parent[ v] = u; vrátiť true; } fronta.push(v); rodič[v] = u; navštívené[v] = pravda; } } } // Nedosiahli sme sink v BFS počnúc // zo zdroja, takže vráťte false return false; } // Vráti maximálny prietok od s do t v // danej grafovej funkcii fordFulkerson(graph, s, t) { nech u, v; // Vytvorte zvyškový graf a vyplňte // zvyškový graf danými kapacitami // v pôvodnom grafe ako zvyškové // kapacity v zvyškovom grafe // Zvyškový graf kde rGraph[i][j] // označuje zvyškovú kapacitu hrany // / od i do j (ak je tam hrana. // Ak je rGraph[i][j] 0, tak // nie je) nech rGraph = new Array(V); for(u = 0; u { rGraph[u] = nové pole(V); for(v = 0; v rGraph[u][v] = graf[u][v]; } // Toto pole je vyplnené BFS a na uloženie cesty nech parent = new Array(V) // Na začiatku nie je žiadny tok nech max_flow = 0 // Rozšíri tok, kým // existuje cesta od zdroja k potope while (bfs(rGraph, s, t); , parent)) { // Nájdite minimálnu zvyškovú kapacitu hrán // pozdĺž cesty vyplnenej BFS Alebo môžeme povedať // nájsť maximálny prietok cez nájdenú cestu nech cesta_tok = Číslo.MAX_HODNOTA pre (v = t ; v != s; v = rodič[v]) { u = tok_cesty = Math.min(cesta_tok, rGraf[u][v] } // Aktualizácia zvyškových kapacít hrán a //); obrátene hrany pozdĺž cesty for(v = t; v != s; v = rodič[v]) { u = rodič[v]] -= tok_cesty[v][u] + = path_flow } // Pridanie toku cesty k celkovému toku max_flow += cesta_tok } // Návrat celkového toku max_flow } // Kód ovládača // Vytvorme graf zobrazený v príklade vyššie nech graf = [ [ 0 , 16, 13, 0, 0, 0 ], [ 0, 0, 10, 12, 0, 0 ], [ 0, 4, 0, 0, 14, 0 ], [ 0, 0, 9, 0, 0 20], [0, 0, 0, 7, 0, 4], [0, 0, 0, 0, 0, 0]]; document.write('Maximálny možný tok je ' + fordFulkerson(graf, 0, 5)); // Tento kód prispel avanitrachhadiya2155> |
>
>Výkon
preity zinta
The maximum possible flow is 23>
Časová zložitosť: O(|V| * E^2) ,kde E je počet hrán a V je počet vrcholov.
Priestorová zložitosť :O(V), ako sme vytvorili front.
Vyššie uvedená implementácia Ford Fulkerson Algorithm je tzv Edmondsov-Karpov algoritmus . Myšlienkou Edmonds-Karp je použiť BFS v implementácii Ford Fulkerson, pretože BFS vždy vyberie cestu s minimálnym počtom hrán. Keď sa použije BFS, časová zložitosť v najhoršom prípade sa môže znížiť na O(VE2). Vyššie uvedená implementácia používa reprezentáciu matice susednosti, hoci BFS berie O(V2) čas, časová náročnosť vyššie uvedenej implementácie je O(EV3) (Odkaz kniha CLRS na dôkaz časovej náročnosti)
Toto je dôležitý problém, ktorý vzniká v mnohých praktických situáciách. Príklady zahŕňajú maximalizáciu prepravy s danými prevádzkovými limitmi, maximalizáciu toku paketov v počítačových sieťach.
Dincov algoritmus pre maximálny prietok.
Cvičenie:
Upravte vyššie uvedenú implementáciu tak, aby bežala v O(VE2) čas.
