Vzhľadom na mriežku s číslami nájdite maximálnu sekvenciu hadích a vytlačte ju. Ak existuje viac hadích sekvencií s maximálnou dĺžkou, vytlačte niektorú z nich.
nastavenia webového prehliadača
Sekvencia hadov sa skladá zo susedných čísel v mriežke tak, že pre každé číslo je číslo vpravo alebo číslo pod ňou +1 alebo -1 jeho hodnota. Napríklad, ak ste na mieste (x y) v mriežke, môžete sa buď pohybovať doprava, t. J. (x y+1), ak je toto číslo ± 1 alebo posuňte nadol, t.j. (x+1 y), ak je toto číslo ± 1.
For example 9 6 5 2 8 7 6 5 7 3 1 6 1 1 1 7 In above grid the longest snake sequence is: (9 8 7 6 5 6 7)
Nižšie je uvedené všetky možné cesty:
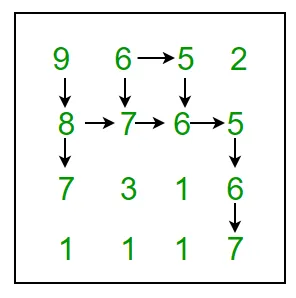
Dôrazne vám odporúčame, aby ste minimalizovali váš prehliadač a vyskúšali si to najskôr sami.
Cieľom je použiť dynamické programovanie. Pre každú bunku matrice udržiavame maximálnu dĺžku hada, ktorý končí v súčasnej bunke. Maximálna dĺžka hadej sekvencie bude mať maximálnu hodnotu. Bunka maximálnej hodnoty bude zodpovedať chvostu hada. Aby sme vytlačili hada, musíme sa vrátiť od chvosta až po Snakeovu hlavu.
aký je rozdiel medzi megabajtom a gigabajtom
Let T[i][i] represent maximum length of a snake which ends at cell (i j) then for given matrix M the DP relation is defined as T[0][0] = 0 T[i][j] = max(T[i][j] T[i][j - 1] + 1) if M[i][j] = M[i][j - 1] ± 1 T[i][j] = max(T[i][j] T[i - 1][j] + 1) if M[i][j] = M[i - 1][j] ± 1
Nižšie je implementácia myšlienky
C++// C++ program to find maximum length // Snake sequence and print it #include
// Java program to find maximum length // Snake sequence and print it import java.util.*; class GFG { static int M = 4; static int N = 4; static class Point { int x y; public Point(int x int y) { this.x = x; this.y = y; } }; // Function to find maximum length Snake sequence path // (i j) corresponds to tail of the snake static List<Point> findPath(int grid[][] int mat[][] int i int j) { List<Point> path = new LinkedList<>(); Point pt = new Point(i j); path.add(0 pt); while (grid[i][j] != 0) { if (i > 0 && grid[i][j] - 1 == grid[i - 1][j]) { pt = new Point(i - 1 j); path.add(0 pt); i--; } else if (j > 0 && grid[i][j] - 1 == grid[i][j - 1]) { pt = new Point(i j - 1); path.add(0 pt); j--; } } return path; } // Function to find maximum length Snake sequence static void findSnakeSequence(int mat[][]) { // table to store results of subproblems int [][]lookup = new int[M][N]; // initialize by 0 // stores maximum length of Snake sequence int max_len = 0; // store coordinates to snake's tail int max_row = 0; int max_col = 0; // fill the table in bottom-up fashion for (int i = 0; i < M; i++) { for (int j = 0; j < N; j++) { // do except for (0 0) cell if (i != 0 || j != 0) { // look above if (i > 0 && Math.abs(mat[i - 1][j] - mat[i][j]) == 1) { lookup[i][j] = Math.max(lookup[i][j] lookup[i - 1][j] + 1); if (max_len < lookup[i][j]) { max_len = lookup[i][j]; max_row = i; max_col = j; } } // look left if (j > 0 && Math.abs(mat[i][j - 1] - mat[i][j]) == 1) { lookup[i][j] = Math.max(lookup[i][j] lookup[i][j - 1] + 1); if (max_len < lookup[i][j]) { max_len = lookup[i][j]; max_row = i; max_col = j; } } } } } System.out.print('Maximum length of Snake ' + 'sequence is: ' + max_len + 'n'); // find maximum length Snake sequence path List<Point> path = findPath(lookup mat max_row max_col); System.out.print('Snake sequence is:'); for (Point it : path) System.out.print('n' + mat[it.x][it.y] + ' (' + it.x + ' ' + it.y + ')'); } // Driver code public static void main(String[] args) { int mat[][] = {{9 6 5 2} {8 7 6 5} {7 3 1 6} {1 1 1 7}}; findSnakeSequence(mat); } } // This code is contributed by 29AjayKumar
// C# program to find maximum length // Snake sequence and print it using System; using System.Collections.Generic; class GFG { static int M = 4; static int N = 4; public class Point { public int x y; public Point(int x int y) { this.x = x; this.y = y; } }; // Function to find maximum length Snake sequence path // (i j) corresponds to tail of the snake static List<Point> findPath(int[ ] grid int[ ] mat int i int j) { List<Point> path = new List<Point>(); Point pt = new Point(i j); path.Insert(0 pt); while (grid[i j] != 0) { if (i > 0 && grid[i j] - 1 == grid[i - 1 j]) { pt = new Point(i - 1 j); path.Insert(0 pt); i--; } else if (j > 0 && grid[i j] - 1 == grid[i j - 1]) { pt = new Point(i j - 1); path.Insert(0 pt); j--; } } return path; } // Function to find maximum length Snake sequence static void findSnakeSequence(int[ ] mat) { // table to store results of subproblems int[ ] lookup = new int[M N]; // initialize by 0 // stores maximum length of Snake sequence int max_len = 0; // store coordinates to snake's tail int max_row = 0; int max_col = 0; // fill the table in bottom-up fashion for (int i = 0; i < M; i++) { for (int j = 0; j < N; j++) { // do except for (0 0) cell if (i != 0 || j != 0) { // look above if (i > 0 && Math.Abs(mat[i - 1 j] - mat[i j]) == 1) { lookup[i j] = Math.Max( lookup[i j] lookup[i - 1 j] + 1); if (max_len < lookup[i j]) { max_len = lookup[i j]; max_row = i; max_col = j; } } // look left if (j > 0 && Math.Abs(mat[i j - 1] - mat[i j]) == 1) { lookup[i j] = Math.Max( lookup[i j] lookup[i j - 1] + 1); if (max_len < lookup[i j]) { max_len = lookup[i j]; max_row = i; max_col = j; } } } } } Console.Write('Maximum length of Snake ' + 'sequence is: ' + max_len + 'n'); // find maximum length Snake sequence path List<Point> path = findPath(lookup mat max_row max_col); Console.Write('Snake sequence is:'); foreach(Point it in path) Console.Write('n' + mat[it.x it.y] + ' (' + it.x + ' ' + it.y + ')'); } // Driver code public static void Main(String[] args) { int[ ] mat = { { 9 6 5 2 } { 8 7 6 5 } { 7 3 1 6 } { 1 1 1 7 } }; findSnakeSequence(mat); } } // This code is contributed by Princi Singh
def snakesequence(S m n): sequence = {} DP = [[1 for x in range(m+1)] for x in range(n+1)] a b maximum = 0 0 0 position = [0 0] for i in range(0 n+1): for j in range(0 m+1): a b = 0 0 p = 'initial' if(i > 0 and abs(S[i][j] - S[i-1][j]) == 1): a = DP[i-1][j] if(j > 0 and abs(S[i][j] - S[i][j-1]) == 1): b = DP[i][j-1] if a != 0 and a >= b: p = str(i-1) + ' ' + str(j) elif b != 0: p = str(i) + ' ' + str(j-1) q = str(i) + ' ' + str(j) sequence[q] = p DP[i][j] = DP[i][j] + max(a b) if DP[i][j] >= maximum: maximum = DP[i][j] position[0] = i position[1] = j snakeValues = [] snakePositions = [] snakeValues.append(S[position[0]][position[1]]) check = 'found' str_next = str(position[0]) + ' ' + str(position[1]) findingIndices = sequence[str_next].split() while(check == 'found'): if sequence[str_next] == 'initial': snakePositions.insert(0 str_next) check = 'end' continue findingIndices = sequence[str_next].split() g = int(findingIndices[0]) h = int(findingIndices[1]) snakeValues.insert(0 S[g][h]) snake_position = str(g) + ' ' + str(h) snakePositions.insert(0 str_next) str_next = sequence[str_next] return [snakeValues snakePositions] S = [[9 6 5 2] [8 7 6 5] [7 3 1 6] [1 1 10 7]] m = 3 n = 3 seq = snakesequence(S m n) for i in range(len(seq[0])): print(seq[0][i] '' seq[1][i].split())
function snakesequence(S m n) { let sequence = {} let DP = new Array(n + 1) for (var i = 0; i <= n; i++) DP[i] = new Array(m + 1).fill(1) let a = 0 b = 0 maximum = 0 let position = [0 0] for (var i = 0; i <= n; i++) { for (var j = 0; j <= m; j++) { a = 0 b = 0 let p = 'initial' if(i > 0 && Math.abs(S[i][j] - S[i-1][j]) == 1) a = DP[i-1][j] if(j > 0 && Math.abs(S[i][j] - S[i][j-1]) == 1) b = DP[i][j-1] if (a != 0 && a >= b) p = String(i-1) + ' ' + String(j) else if (b != 0) p = String(i) + ' ' + String(j-1) let q = String(i) + ' ' + String(j) sequence[q] = p DP[i][j] = DP[i][j] + Math.max(a b) if (DP[i][j] >= maximum) { maximum = DP[i][j] position[0] = i position[1] = j } } } let snakeValues = [] let snakePositions = [] snakeValues.push(S[position[0]][position[1]]) let check = 'found' let String_next = String(position[0]) + ' ' + String(position[1]) let findingIndices = sequence[String_next].split(' ') while(check == 'found') { if (sequence[String_next] == 'initial') { snakePositions.unshift(String_next) check = 'end' continue } findingIndices = sequence[String_next].split(' ') let g = parseInt(findingIndices[0]) let h = parseInt(findingIndices[1]) snakeValues.unshift(S[g][h]) let snake_position = String(g) + ' ' + String(h) snakePositions.unshift(String_next) String_next = sequence[String_next] } return [snakeValues snakePositions] } // Driver Code let S = [[9 6 5 2] [8 7 6 5] [7 3 1 6] [1 1 10 7]] let m = 3 let n = 3 let seq = snakesequence(S m n) for (var i = 0; i < seq[0].length; i++) console.log(seq[0][i] + '' seq[1][i].split(' '))
Výstup
Maximum length of Snake sequence is: 6 Snake sequence is: 9 (0 0) 8 (1 0) 7 (1 1) 6 (1 2) 5 (1 3) 6 (2 3) 7 (3 3)
Časová zložitosť vyššie uvedeného roztoku je O (m*n). Pomocný priestor použitý vyššie uvedeným roztokom je O (m*n). Ak sa nemusíme tlačiť na hadí priestor, sa dá ďalej zredukovať na O (n), pretože výsledok používame iba z posledného riadku.
