- Algoritmus vektora vzdialenosti je dynamický algoritmus.
- Používa sa hlavne v ARPANET a RIP.
- Každý smerovač udržiava tabuľku vzdialeností, tzv Vektor .
Tri kľúče na pochopenie fungovania algoritmu smerovania vektorov vzdialenosti:
Algoritmus smerovania vektorov vzdialenosti
Nech dX(y) sú náklady na cestu s najnižšími nákladmi z uzla x do uzla y. Najnižšie náklady súvisia s Bellman-Fordovou rovnicou,
d<sub>x</sub>(y) = min<sub>v</sub>{c(x,v) + d<sub>v</sub>(y)} Kde minv je rovnica prijatá pre všetkých x susedov. Po cestovaní z x do v, ak vezmeme do úvahy najlacnejšiu cestu z v do y, cena cesty bude c(x,v)+dv(y). Najnižšia cena od x do y je minimum c(x,v)+dv(y) prevzal všetkých susedov.
S algoritmom smerovania vektorov vzdialenosti obsahuje uzol x nasledujúce informácie o smerovaní:
- Pre každého suseda v sú náklady c(x,v) náklady na cestu od x k priamo pripojenému susedovi v.
- Vektor vzdialenosti x, t.j. DX= [DX(y) : y v N ], ktoré obsahuje jeho náklady na všetky miesta určenia, y, v N.
- Vektor vzdialenosti každého z jeho susedov, t.j. Dv= [Dv(y): y v N ] pre každého suseda v z x.
Smerovanie vektora vzdialenosti je asynchrónny algoritmus, v ktorom uzol x posiela kópiu svojho vektora vzdialenosti všetkým svojim susedom. Keď uzol x prijme nový vektor vzdialenosti od jedného zo svojich susedných vektorov, v, uloží vektor vzdialenosti v a použije Bellman-Fordovu rovnicu na aktualizáciu vlastného vektora vzdialenosti. Rovnica je uvedená nižšie:
10 1 milióna
d<sub>x</sub>(y) = min<sub>v</sub>{ c(x,v) + d<sub>v</sub>(y)} for each node y in N Uzol x aktualizoval svoju vlastnú tabuľku vektorov vzdialeností pomocou vyššie uvedenej rovnice a posiela svoju aktualizovanú tabuľku všetkým svojim susedom, aby mohli aktualizovať svoje vlastné vektory vzdialeností.
Algoritmus
At each node x, <p> <strong>Initialization</strong> </p> for all destinations y in N: D<sub>x</sub>(y) = c(x,y) // If y is not a neighbor then c(x,y) = ∞ for each neighbor w D<sub>w</sub>(y) = ? for all destination y in N. for each neighbor w send distance vector D<sub>x</sub> = [ D<sub>x</sub>(y) : y in N ] to w <strong>loop</strong> <strong>wait</strong> (until I receive any distance vector from some neighbor w) for each y in N: D<sub>x</sub>(y) = minv{c(x,v)+D<sub>v</sub>(y)} If D<sub>x</sub>(y) is changed for any destination y Send distance vector D<sub>x</sub> = [ D<sub>x</sub>(y) : y in N ] to all neighbors <strong>forever</strong> Poznámka: V algoritme vektora vzdialenosti, uzol x aktualizuje svoju tabuľku, keď buď uvidí akúkoľvek zmenu nákladov v jednom priamo prepojenom uzle, alebo dostane akúkoľvek aktualizáciu vektora od nejakého suseda.
Poďme to pochopiť na príklade:
Zdieľanie informácií
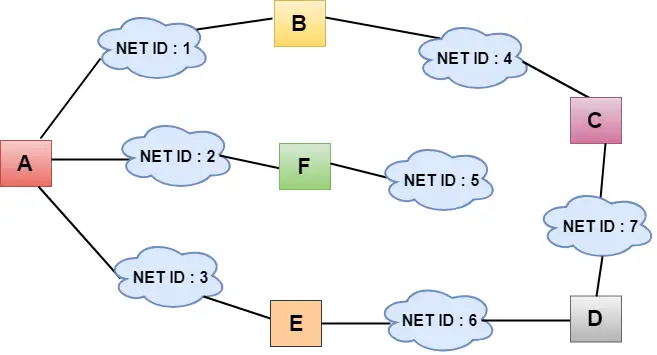
- Na obrázku vyššie každý cloud predstavuje sieť a číslo vnútri cloudu predstavuje ID siete.
- Všetky siete LAN sú prepojené smerovačmi a sú zobrazené v rámčekoch označených ako A, B, C, D, E, F.
- Algoritmus vektorového smerovania vzdialenosti zjednodušuje proces smerovania tým, že predpokladá, že cena každého spojenia je jedna jednotka. Efektívnosť prenosu sa preto dá merať počtom spojení na dosiahnutie cieľa.
- Pri vektorovom smerovaní vzdialenosti sú náklady založené na počte skokov.

Na obrázku vyššie vidíme, že smerovač posiela poznatky k bezprostredným susedom. Susedia pridajú tieto poznatky k svojim vlastným znalostiam a pošlú aktualizovanú tabuľku svojim vlastným susedom. Týmto spôsobom smerovače získajú svoje vlastné informácie plus nové informácie o susedoch.
Smerovacia tabuľka
Vyskytujú sa dva procesy:
- Vytvorenie tabuľky
- Aktualizácia tabuľky
Vytvorenie tabuľky
Na začiatku sa pre každý smerovač vytvorí smerovacia tabuľka, ktorá obsahuje aspoň tri typy informácií, ako je ID siete, cena a ďalší skok.


- Na obrázku vyššie sú zobrazené pôvodné smerovacie tabuľky všetkých smerovačov. V smerovacej tabuľke prvý stĺpec predstavuje ID siete, druhý stĺpec predstavuje náklady na prepojenie a tretí stĺpec je prázdny.
- Tieto smerovacie tabuľky sa posielajú všetkým susedom.
Napríklad:
A sends its routing table to B, F & E. B sends its routing table to A & C. C sends its routing table to B & D. D sends its routing table to E & C. E sends its routing table to A & D. F sends its routing table to A.
Aktualizácia tabuľky
- Keď A dostane smerovaciu tabuľku od B, potom použije jej informácie na aktualizáciu tabuľky.
- Smerovacia tabuľka B ukazuje, ako sa pakety môžu presúvať do sietí 1 a 4.
- B je sused s routerom A, pakety z A do B sa môžu dostať jedným skokom. Takže 1 sa pripočíta ku všetkým nákladom uvedeným v tabuľke B a súčet budú náklady na dosiahnutie konkrétnej siete.

- Po úprave potom A skombinuje túto tabuľku s vlastnou tabuľkou a vytvorí kombinovanú tabuľku.

- Kombinovaná tabuľka môže obsahovať niektoré duplicitné údaje. Na obrázku vyššie obsahuje kombinovaná tabuľka smerovača A duplicitné údaje, takže uchováva iba tie údaje, ktoré majú najnižšie náklady. Napríklad A môže odosielať údaje do siete 1 dvoma spôsobmi. Prvý, ktorý nepoužíva ďalší smerovač, takže stojí jeden skok. Druhý vyžaduje dva skoky (A na B, potom B na sieť 1). Prvá možnosť má najnižšie náklady, preto sa ponechá a od druhej sa upustí.

- Proces vytvárania smerovacej tabuľky pokračuje pre všetky smerovače. Každý smerovač prijíma informácie od susedov a aktualizuje smerovaciu tabuľku.
Konečné smerovacie tabuľky všetkých smerovačov sú uvedené nižšie:

