Trigonometria je dôležité odvetvie matematiky, ktoré sa zaoberá vzťahom medzi dĺžkami strán a uhlami pravouhlého trojuholníka. Sínus, kosínus, tangens, kosekans, sekans a kotangens je šesť trigonometrických pomerov alebo funkcií. Kde je trigonometrický pomer znázornený ako pomer medzi stranami pravouhlého trojuholníka.

• sin θ = opačná strana/hypotenza
• cos θ = susedná strana/hypotenza
• tan θ = opačná strana/susedná strana
• cosec θ = 1/sin θ = prepona/opačná strana
• sek θ = 1/cos θ = prepona/susedná strana
• detská postieľka θ = 1/tan θ = susedná strana/protiľahlá strana

Kotangensový vzorec

Funkcia kotangens je recipročná funkcia danej dotyčnicovej funkcie. Hodnota kotangensového uhla v pravouhlom trojuholníku je pomer dĺžky strany susediacej s daným uhlom k dĺžke protiľahlej strany k danému uhlu. Kotangens funkciu píšeme ako kotangens.

Trojuholník ABC

Kotangens vzorec pre uhol θ je teraz,

detská postieľka θ = (priľahlá strana)/(opačná strana)

• Funkcia kotangens je kladná v prvom a treťom kvadrante a záporná v druhom a štvrtom kvadrante.

1. detská postieľka (2π + θ) = detská postieľka θ (1^svkvadrant)
2. detská postieľka (π – θ) = – detská postieľka θ (2^ndkvadrant)
3. detská postieľka (π + θ) = detská postieľka θ (3^rdkvadrant)
4. detská postieľka (2π – θ) = – detská postieľka θ (4^thkvadrant)

• Kotangens funkcia je negatívna funkcia, pretože kotangens záporného uhla je záporný kotangens kladného uhla.

detská postieľka (-θ) = – detská postieľka θ

• Z hľadiska funkcie tangens je funkcia kotangens napísaná ako,

detská postieľka 9 = 1/tan 9

(alebo)

if else príkaz java

detská postieľka θ = tan (90° – θ) (alebo) tan (π/2 – θ)

• Funkciu kotangens z hľadiska funkcií sínus a kosínus možno zapísať ako,

detská postieľka θ = cos θ/sin θ

Vieme, že detská postieľka θ = susedná strana/protiľahlá strana

Teraz rozdeľte čitateľa aj menovateľa s preponou

⇒ detská postieľka θ = (priľahlá strana/hypotenza) / (opačná strana/hypotenza)

Vieme, že sin θ = opačná strana/hypotenúza

cos θ = susedná strana/hypotenza

Preto detská postieľka θ = cos θ/sin θ

• Funkciu kotangens z hľadiska funkcie sínus možno napísať ako,

detská postieľka θ = (√1 – sin ² i)/sin i

Vieme, že čot θ = cos θ/sin θ

Z pytagorovských identít, ktoré máme;

cos²θ + hriech²θ = 1

⇒ cos θ = √1 – hriech²i

Preto detská postieľka θ =

• Funkciu kotangens z hľadiska kosínusovej funkcie možno zapísať ako,

detská postieľka θ = cos θ/(√1 -cos ² i)

Vieme, že čot θ = cos θ/sin θ

Z pytagorovských identít, ktoré máme;

cos²θ + hriech²θ = 1

sin θ = √1 – cos²i

Preto detská postieľka θ =

• Funkciu kotangens z hľadiska funkcií sekans a kosekans možno písať ako,

detská postieľka θ = cosec θ/sec θ

Máme, detská postieľka θ = cos θ/sin θ

Dá sa to napísať ako, detská postieľka θ = (1/sin θ) / (1/cos θ)

⇒ detská postieľka θ = cosec θ/sec θ

• Funkciu kotangens z hľadiska funkcie kosekans možno zapísať ako:

detská postieľka θ = √ (kosec ² - 1)

Z pytagorovských identít máme,

cosec²θ – detská postieľka²θ = 1

⇒ detská postieľka²θ = 1 – kosec²- 1

Preto detská postieľka θ = √(cosec²- 1)

• Funkciu kotangens z hľadiska funkcie sekansu možno zapísať ako:

detská postieľka θ = 1/(√sek ² ja – 1)

Z pytagorovských identít máme,

sek²θ – teda²θ = 1

tan θ = √sek²ja – 1

Vieme, že detská postieľka θ = 1/tan θ

teda detská postieľka θ =

Trigonometrická pomerová tabuľka

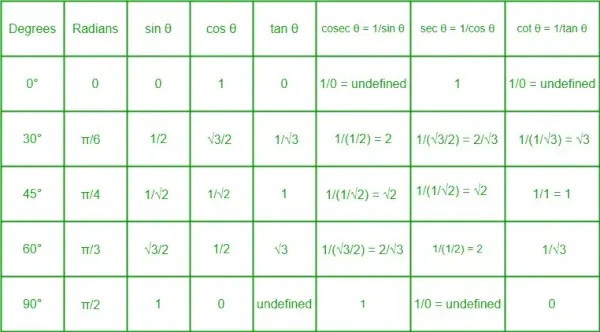
Tabuľka trigonometrických pomerov

Zákon kotangens alebo zákon kotangens

Zákon kotangens vyzerá podobne ako zákon sínus, ale tu zahŕňa polovičné uhly. Zákon kotangens popisuje vzťah medzi dĺžkami strán trojuholníka a kotangens polovíc troch uhlov. Uvažujme trojuholník ABC, kde a, b a c sú dĺžky strán trojuholníka.

Zákon kotangens hovorí, že

Kde s je polobvod trojuholníka ABC a r je jeho polomer kružnice vpísanej trojuholníku.

s = (a + b + c)/2

r =

Ukážkové problémy

Úloha 1: Nájdite hodnotu detskej postieľky θ, ak tan θ = 3/4.

Riešenie:

Dané údaje, tan θ = 3/4

My to vieme, detská postieľka 9 = 1/tan 9

⇒ postieľka θ = 1/(3/4) = 4/3

Takže detská postieľka θ = 4/3

Úloha 2: Nájdite hodnotu cot α, sin α = 1/3 a cos α = 2√2/3.

Riešenie:

Dané údaje, sin α = 1/3 a cos α = 2√2/3

My to vieme, detská postieľka α = cos α/sin α

⇒ detská postieľka α = (2√2/3) / (1/3) = 2√2

java trieda matematiky

Preto hodnota detskej postieľky α = 2√2

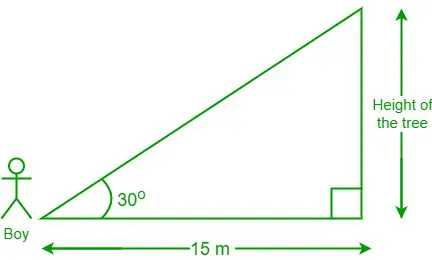
Úloha 3: Chlapec stojaci 15 m od stromu sa pozerá na vrchol stromu v 30-stupňovom uhle. Aká je výška stromu?

Riešenie:

Diagram z uvedených údajov

Podľa údajov je vzdialenosť medzi chlapcom a pätou stromu = 15 m a θ = 30°

Nech je výška stromu „h“

Máme, detská postieľka θ = susedná strana/protiľahlá strana

⇒ postieľka 30° = 15/hod

⇒ √3 = 15/h [keďže, postieľka 30° = √3]

⇒ h = 15/√3

⇒ h = 5√3 m

Preto výška stromu = 5√3 m

ako odkryť aplikáciu v systéme Android

Úloha 4: Nájdite hodnotu postieľky x, ak sek x = 6/5.

Riešenie:

Dané údaje, sek x = 6/5

Máme, sek ² x – teda ² x = 1

⇒ (6/5)²- tak²x = 1

⇒ 36/25 – tak²x = 1

⇒ teda²x = 36/25 – 1

⇒ teda²x = 11/25

⇒ tan x = √(11/25) = √11/5

My to vieme, detská postieľka x = 1/opálenie x

⇒ detská postieľka x = 1/(√11/5) = 5/√11

Preto postieľka x = 5/√11

Úloha 5: Nájdite hodnotu cot θ, ak cosec θ = 25/24.

Riešenie:

Dané údaje, cosec θ = 25/24

My to vieme, detská postieľka θ = √ (kosec ² - 1)

⇒ detská postieľka θ = √ (25/24)²- 1

⇒ detská postieľka θ =√(625 – 576)/576 = √49/576

⇒ detská postieľka θ = 7/24

Preto hodnota detskej postieľky θ = 7/24

Úloha 6: Nájdite hodnotu detskej postieľky β, ak sin β = 5/13.

Riešenie:

Dané údaje, sin β = 5/13

My to vieme, bez ² β + cos ² β = 1

⇒ (5/13)²+ cos²β = 1

⇒ cos²β = 1 – (5/13)²= 1 – 25/169 = 144/169

⇒ cos β = √144/169 = 12/13

detská postieľka β = cosβ/sin β

= (12/13) / (5/13)

⇒ detská postieľka β = 12/5

Preto hodnota detskej postieľky β = 12/5

bash premenná

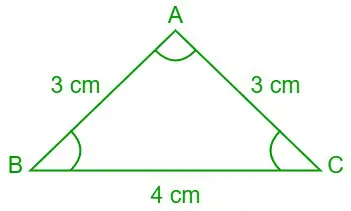
Úloha 7: Pomocou zákona kotangens nájdite hodnoty ∠A, ∠B a ∠C (v stupňoch), ak sú dĺžky troch strán trojuholníka ABC a = 4 cm, b = 3 cm a c= 3 cm.

Riešenie:

Dané, a = 4 cm, b = 3 cm a c = 3 cm

Trojuholník ABC

Zo zákona kotangens,

s = (a + b + c)/2

⇒ s = (3 + 4 + 3)/2 = 10/2 = 5

Teraz s – a = 5 – 4 = 1

⇒ s – b = 5 – 3 = 2

⇒ s – c = 5 – 3 = 2

r =

⇒ r = √[(1)(2)(2)/5]

Polomer trojuholníka r = 2/√5

Z rovnice zákona kotangens,

detská postieľka (A/2)/1 = 1/(2/√5)

⇒ postieľka (A/2) = √5/2 ⇒ A/2 = detská postieľka^-1(√5/2)

⇒ (A/2) = 41,8° ⇒ ∠A = 83,6°

detská postieľka(B/2)/2 = 1/(2/√5)

⇒ postieľka (B/2)/2 = √5/2 ⇒ postieľka (B/2) = √5

⇒ (B/2) = detská postieľka^-1(√5) = 24,1° ⇒ ∠B = 48,2°

detská postieľka (C/2)/2 = 1/(2/√5)

⇒ postieľka(C/2) = √5 ⇒ (C/2) = detská postieľka^-1(√5)

⇒ (C/2) = 24,1° ⇒ ∠C = 48,2°

Uhly trojuholníka ABC sú teda ∠A = 83,6°, ∠B = 48,2° a ∠C = 48,2°.