Vieme a strom je nelineárna dátová štruktúra. Počet detí nie je obmedzený. AČo je úplný binárny strom?
Úplný binárny strom je špeciálny typ binárneho stromu, kde sú všetky úrovne stromu úplne vyplnené okrem uzlov najnižšej úrovne, ktoré sú vyplnené čo najviac zľava.

Kompletný binárny strom
Niektoré terminológie úplného binárneho stromu:
- Root – Uzol, v ktorom žiadna hrana neprichádza z rodiča. Príklad - uzol A
- Dieťa – Uzol s nejakou vstupnou hranou sa nazýva dieťa. Príklad – uzly B, F sú potomkami uzlov A a C.
- Súrodenec – Uzly s rovnakým rodičom sú súrodenci. Príklad - D, E sú súrodenci, pretože majú rovnakého rodiča B.
- Stupeň uzla – Počet detí konkrétneho rodiča. Príklad – Stupeň A je 2 a Stupeň C je 1. Stupeň D je 0.
- Interné/Externé uzly – Listové uzly sú vonkajšie uzly a nelistové uzly sú vnútorné uzly.
- úroveň – Spočítajte uzly na ceste, aby ste dosiahli cieľový uzol. Príklad - Úroveň uzla D je 2, pretože uzly A a B tvoria cestu.
- Výška – Počet hrán na dosiahnutie cieľového uzla, Koreň je vo výške 0. Príklad – Výška uzla E je 2, keďže má dve hrany od koreňa.
Vlastnosti kompletného binárneho stromu:
- O úplnom binárnom strome sa hovorí, že je to správny binárny strom, kde všetky listy majú rovnakú hĺbku.
- V úplnom binárnom strome počet uzlov v hĺbke d je 2 d .
- V kompletnom binárnom strome s n uzly výška stromu je log(n+1) .
- Všetky úrovne okrem poslednej úrovne sú úplne plné.
Perfektný binárny strom vs Kompletný binárny strom:
Binárny strom výšky „h“ s maximálnym počtom uzlov je a perfektné binárny strom.
Pre danú výšku h , maximálny počet uzlov je 2 h+1 -1 .
A kompletný binárny strom výšky h je dokonalý binárny strom do výšky h-1 a v prvku poslednej úrovne sú uložené v poradí zľava doprava.
Príklad 1:
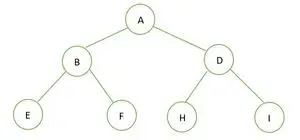
Binárny strom
Výška daného binárneho stromu je 2 a maximálny počet uzlov v tomto strome je n=2h+1-1 = 22+1-1 = 23-1 = 7 .
Preto môžeme konštatovať, že áno dokonalý binárny strom .
Teraz pre úplný binárny strom, je plný až do výšky h-1 t.j.; 1 a prvky poslednej úrovne sú uložené v poradí zľava doprava. Preto je to tiež úplný binárny strom. Tu je znázornenie prvkov, keď sú uložené v poli

Prvok uložený v poli úroveň po úrovni
V poli sú všetky prvky uložené nepretržite.
Príklad 2:
rodič jquery
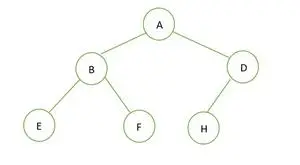
Binárny strom
Výška daného binárneho stromu je 2 a maximálny počet uzlov, ktoré tam majú byť, sú 2h+1– 1 = 22+1– 1 = 23– 1 = 7 .
Ale počet uzlov v strome je 6 . Preto je nie je to dokonalý binárny strom .
Teraz pre úplný binárny strom, je plný až do výšky h-1 t.j.; 1 a posledný prvok úrovne sú uložené v poradí zľava doprava. Toto je teda a úplný binárny strom . Uložte prvok do poľa a bude to ako;
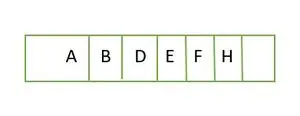
Prvok uložený v poli úroveň po úrovni
Príklad 3:
Madhuri povedal poď
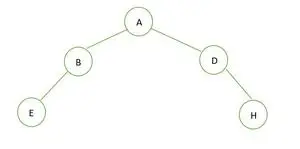
Binárny strom
Výška binárneho stromu je 2 a maximálny počet uzlov, ktoré tam môžu byť, je 7, ale existuje iba 5 uzlov, preto je nie je to dokonalý binárny strom .
V prípade úplného binárneho stromu vidíme, že v poslednej úrovni sa prvky nevypĺňajú zľava doprava. Tak to je nie je úplný binárny strom .
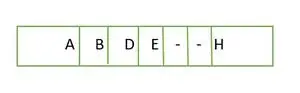
Prvok uložený v poli úroveň po úrovni
Prvky v poli nie sú súvislé.
Úplný binárny strom verzus úplný binárny strom:
Pre úplný binárny strom má každý uzol buď 2 deti, alebo 0 detí.
Príklad 1:
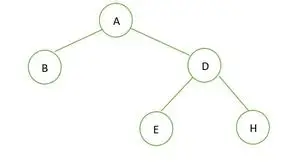
Binárny strom
V danom binárnom strome nie je žiadny uzol, ktorý by mal stupeň 1, buď 2 alebo 0 potomkov pre každý uzol, preto je úplný binárny strom .
Pre úplný binárny strom sa prvky ukladajú na úrovni po úrovni a nie z ľavej strany na poslednej úrovni. Preto toto je nie je úplný binárny strom . Reprezentácia poľa je:
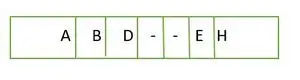
Prvok uložený v poli úroveň po úrovni
Príklad 2:
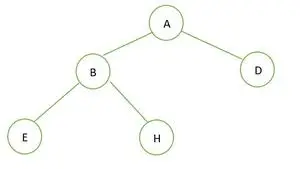
Binárny strom
V danom binárnom strome nie je žiadny uzol so stupňom 1. Každý uzol má stupeň 2 alebo 0. Ide teda o úplný binárny strom .
Pre úplný binárny strom sa prvky ukladajú po jednotlivých úrovniach a vypĺňajú sa z ľavej strany poslednej úrovne. Preto toto a úplný binárny strom . Nižšie je znázornenie poľa stromu:
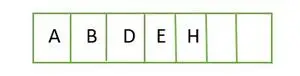
Prvok uložený v poli úroveň po úrovni
Príklad 3:
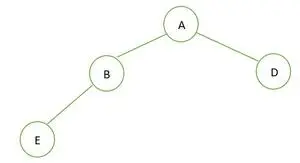
Binárny strom
V danom binárnom strome má uzol B stupeň 1, ktorý porušuje vlastnosť úplného binárneho stromu, preto je nie je úplný binárny strom
bash if vyhlásenie
Pre úplný binárny strom sa prvky ukladajú spôsobom podľa úrovní a vypĺňajú sa z ľavej strany poslednej úrovne. Toto je teda a úplný binárny strom . Reprezentácia poľa binárneho stromu je:
zoznam na java
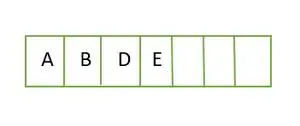
Prvok uložený v poli úroveň po úrovni
Príklad 4:
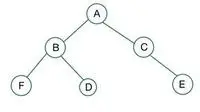
binárny strom
V danom binárnom strome má uzol C stupeň 1, ktorý porušuje vlastnosť úplného binárneho stromu, preto je nie je úplný binárny strom
Pre úplný binárny strom sa prvky ukladajú spôsobom podľa úrovní a vypĺňajú sa z ľavej strany poslednej úrovne. Tu uzol E porušuje podmienku. Preto toto je nie je úplný binárny strom .
Vytvorenie kompletného binárneho stromu:
Vieme a úplný binárny strom je strom, v ktorom okrem poslednej úrovne (povedzme l )všetky ostatné úrovne majú ( 2l ) uzly a uzly sú zoradené zľava doprava.
Môže byť reprezentovaný pomocou poľa. Ak je rodičom index i takže ľavé dieťa je pri 2i+1 a správne dieťa je pri 2i+2 .
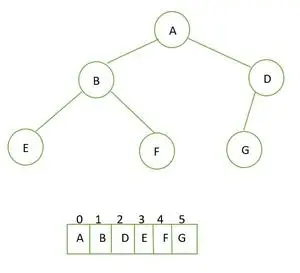
Kompletný binárny strom a jeho reprezentácia poľa
Algoritmus:
Na vytvorenie a Kompletný binárny strom , požadujeme a Krok 1: Inicializujte koreň s novým uzlom, keď je strom prázdny.
Krok 2: Ak strom nie je prázdny, získajte predný prvok
- Ak predný prvok nemá ľavé dieťa, nastavte ľavé dieťa na nový uzol
- Ak nie je prítomné správne dieťa, nastavte správne dieťa ako nový uzol
Krok 3: Ak má uzol obe deti, potom pop to z radu.
knn algoritmus
Krok 4: Zaraďte nové údaje do frontu.
Ilustrácia:
Zvážte nižšie uvedené pole:
1. Prvým prvkom bude koreň (hodnota na indexe = 0 )
A sa berie ako koreň
2. Ďalší prvok (na indexe = 1 ) bude ponechaný a tretí prvok (index = 2 ) bude správnym dieťaťom root
B ako ľavé dieťa a D ako pravé dieťa
3. štvrtý (index = 3 ) a piaty prvok (index = 4 ) bude ľavým a pravým potomkom uzla B
E a F sú ľavé a pravé dieťa B
4. Ďalší prvok (index = 5 ) zostane potomkom uzla D
G je ľavé dieťa uzla D
Takto sa vytvorí kompletný binárny strom.
Implementácia: Pre implementáciu budovania kompletného binárneho stromu z úrovne poradia je uvedené v tento príspevok .
Aplikácia úplného binárneho stromu:
- Hromadné triedenie
- Štruktúra údajov založená na triedení haldy
Skontrolujte, či je daný binárny strom úplný alebo nie: Sledujte tento príspevok skontrolovať, či je daný binárny strom úplný alebo nie.




