Z-SKÓRE V ŠTATISTIKE

Z-skóre v štatistike je meranie toho, koľko štandardných odchýlok má dátový bod od priemeru rozdelenia. Nájdite skóre z v štatistike. Z-skóre 0 znamená, že skóre dátového bodu je rovnaké ako priemerné skóre. Pozitívne z-skóre znamená, že dátový bod je nadpriemerný, zatiaľ čo negatívne z-skóre znamená, že dátový bod je pod priemerom.

Vzorec na výpočet z-skóre je: z = (x – μ)/ p

c boolovská hodnota

Kde:

X: je testovacia hodnota
m: je priemer
na: je štandardná hodnota

V tomto článku budeme diskutovať o nasledujúcich pojmoch:

Obsah

Čo je Z-skóre?
Ako vypočítať Z-skóre?
Charakteristika Z-skóre
Vypočítajte odľahlé hodnoty pomocou hodnoty Z-score
Implementácia Z-Score v Pythone
Aplikácia Z-skóre
Z-skóre vs. štandardná odchýlka
Prečo sa Z-skóre nazývajú štandardné skóre?

Čo je Z-skóre?

Z-skóre, tiež známe ako štandardné skóre, nám hovorí o odchýlke údajového bodu od priemeru tým, že ju vyjadruje ako štandardné odchýlky nad alebo pod priemerom. Poskytuje nám predstavu o tom, ako ďaleko je dátový bod od priemeru. Z-skóre sa teda meria ako štandardná odchýlka od priemeru. Napríklad Z-skóre 2 znamená, že hodnota je 2 štandardné odchýlky od priemeru. Aby sme mohli použiť z-skóre, potrebujeme poznať priemer populácie (μ) a tiež štandardnú odchýlku populácie (σ).

Vzorec pre Z-skóre

Z-skóre možno vypočítať pomocou nasledujúceho vzorca.

z = (X – μ) / p

kde,

z = Z-skóre
X = Hodnota prvku
μ = populačný priemer
σ = smerodajná odchýlka populácie

Ako vypočítať Z-skóre?

Dostaneme priemer populácie (μ), smerodajnú odchýlku populácie (σ) a pozorovanú hodnotu (x) v problémovom vyhlásení, keď to isté nahradíme v rovnici Z-skóre, získame hodnotu Z-skóre. V závislosti od toho, či je dané Z-skóre kladné alebo záporné, môžeme použiť pozitívna Z-tabuľka alebo negatívna Z-tabuľka dostupné online alebo na zadnej strane vašej učebnice štatistiky v prílohe.

Príklad 1:

Absolvujete test GATE a získate 500. Priemerné skóre pre GATE je 390 a štandardná odchýlka je 45. Ako dobre ste dosiahli skóre v teste v porovnaní s priemerným účastníkom testu?

Riešenie:

Nasledujúce údaje sú ľahko dostupné vo vyššie uvedenej otázke

Nespracované skóre/pozorovaná hodnota = X = 500

Priemerné skóre = μ = 390

Smerodajná odchýlka = σ = 45

Použitím vzorca z-skóre,

z = (X – μ) / p

z = (500 – 390) / 45

z = 110/45 = 2,44

reťazec n java

To znamená, že vaše Z-skóre je 2.44 .

Keďže Z-skóre je kladné 2,44, použijeme kladnú Z-tabuľku.

Teraz sa pozrime na Tabuľka Z (CC-BY), aby ste vedeli, ako dobre ste dosiahli v porovnaní s ostatnými účastníkmi testu.

Ak chcete zistiť pravdepodobnosť z tabuľky, postupujte podľa pokynov nižšie.

Tu, z-skóre = 2,44, ktoré i znamená, že dátový bod je 2,44 štandardnej odchýlky nad priemerom.

Najprv zmapujte prvé dve číslice 2.4 na osi Y.
Potom pozdĺž osi X, mapa 0,04
Spojte obe osi. Priesečník oboch vám poskytne kumulatívnu pravdepodobnosť spojenú s hodnotou Z-skóre, ktorú hľadáte

[Táto pravdepodobnosť predstavuje oblasť pod štandardnou normálnou krivkou naľavo od Z-skóre]

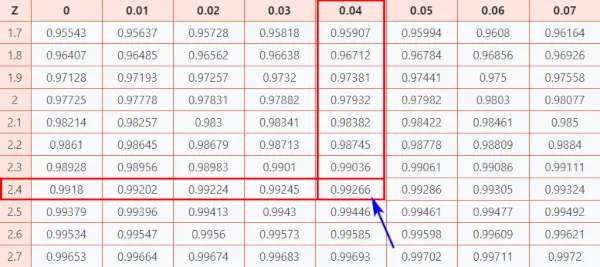
Tabuľka normálneho rozdelenia

V dôsledku toho získate konečnú hodnotu, ktorá je 0,99266 .

Teraz musíme porovnať, ako je naše pôvodné skóre 500 v teste GATE v porovnaní s priemerným skóre dávky. Aby sme to dosiahli, musíme previesť kumulatívnu pravdepodobnosť spojenú so Z-skóre na percentuálnu hodnotu.

0,99266 × 100 = 99,266 %

Nakoniec môžete povedať, že ste podali dobrý výkon 99 % ostatných účastníkov testu.

Príklad 2 : Aká je pravdepodobnosť, že študent dosiahne skóre medzi 350 a 400 (s priemerným skóre μ 390 a štandardnou odchýlkou σ 45)?

Riešenie:

Minimálne skóre = X₁= 350

Maximálne skóre = X₂= 400

Použitím vzorca z-skóre,

S₁= (X1 – m) / p

S₁= (350 – 390) / 45

S₁= -40/45 = -0,88

S₂= (X₂– m) / str

z2 = (400 – 390) / 45

S₂= 10/45 = 0,22
Java referenčné typy

Keďže z1 je záporné, budeme sa musieť pozrieť na zápor Z-Tabuľka a zistite, že kumulatívna pravdepodobnosť p1, prvá pravdepodobnosť, je 0,18943 .

S₂je kladná, preto použijeme kladnú Z-tabuľku, ktorá dáva kumulatívnu pravdepodobnosť p₂z 0,58706 .

Konečná pravdepodobnosť sa vypočíta odčítaním p1 od p₂:

p = p₂– p₁

p = 0,58706 – 0,18943 = 0,39763

Pravdepodobnosť, že študent dosiahne skóre medzi 350 a 400, je 39,763 % (0,39763 x 100).

Charakteristika Z-skóre

Veľkosť Z-skóre odráža, ako ďaleko je dátový bod od priemeru z hľadiska štandardných odchýlok.
Prvok, ktorý má z-skóre menšie ako 0, znamená, že prvok je menší ako priemer.
Z-skóre umožňujú porovnanie údajových bodov z rôznych distribúcií.
Prvok, ktorý má z-skóre väčšie ako 0, znamená, že prvok je väčší ako priemer.
Prvok, ktorý má z-skóre rovné 0, znamená, že prvok sa rovná priemeru.
Prvok, ktorý má z-skóre rovné 1, predstavuje, že prvok je o 1 štandardnú odchýlku väčší ako priemer; z-skóre rovné 2, 2 štandardné odchýlky väčšie ako priemer atď.
Prvok, ktorý má z-skóre rovné -1, predstavuje, že prvok je o 1 štandardnú odchýlku menší ako priemer; z-skóre rovné -2, 2 štandardné odchýlky menšie ako priemer atď.
Ak je počet prvkov v danej množine veľký, potom asi 68 % prvkov má z-skóre medzi -1 a 1; približne 95 % má z-skóre medzi -2 a 2; približne 99 % má z-skóre medzi -3 a 3. Toto je známe ako empirické pravidlo a uvádza percento údajov v rámci určitých štandardných odchýlok od priemeru v normálnom rozdelení, ako je znázornené na obrázku nižšie

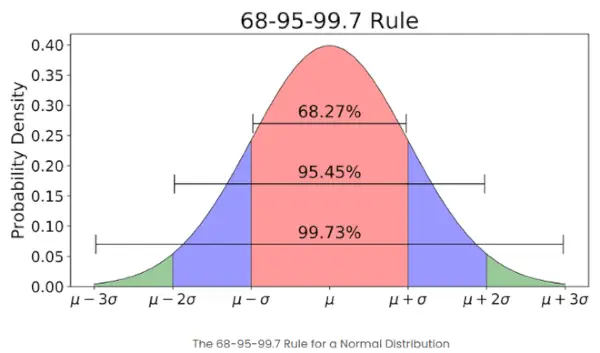
Empirické pravidlo normálneho rozdelenia

Vypočítajte odľahlé hodnoty pomocou hodnoty Z-score

Odľahlé hodnoty v údajoch môžeme vypočítať pomocou hodnoty z-skóre údajových bodov. Kroky na zváženie odľahlého údajového bodu sú nasledovné:

Najprv zhromažďujeme súbor údajov, v ktorom chceme vidieť odľahlé hodnoty
Vypočítame priemer a štandardnú odchýlku súboru údajov. Tieto hodnoty sa použijú na výpočet hodnoty z-skóre každého údajového bodu.
Vypočítame hodnotu z-skóre pre každý dátový bod. Vzorec na výpočet hodnoty z-skóre bude rovnaký ako
Z = frac{{X – mu}}{{sigma}}
kde X bude údajový bod, μ je priemer údajov a σ je štandardná odchýlka súboru údajov.
Určíme hraničnú hodnotu pre z-skóre, po ktorej by sa dátový bod mohol považovať za odľahlú hodnotu. Táto medzná hodnota je hyperparameter, o ktorom rozhodujeme v závislosti od nášho projektu.
Údajový bod, ktorého hodnota z-skóre je väčšia ako 3 znamená, že údajový bod nepatrí do 99,73 % bodu súboru údajov.
Akýkoľvek údajový bod, ktorého z-skóre je väčšie ako naša stanovená medzná hodnota, sa bude považovať za odľahlú hodnotu.

Skontrolujte: Skóre Z pre detekciu odľahlých hodnôt

Implementácia Z-Score v Pythone

Python môžeme použiť na výpočet hodnoty z-score dátových bodov v množine údajov. Tiež použijeme numpy knižnicu na výpočet strednej a štandardnej odchýlky súboru údajov.

Python3

 import numpy as np def calculate_z_score(data): # Mean of the dataset mean = np.mean(data) # Standard Deviation of tha dataset std_dev = np.std(data) # Z-score of tha data points z_scores = (data - mean) / std_dev return z_scores # Example dataset dataset = [3,9, 23, 43,53, 4, 5,30, 35, 50, 70, 150, 6, 7, 8, 9, 10] z_scores = calculate_z_score(dataset) print('Z-Score :',z_scores) # Data points which lies outside 3 standard deviatioms are outliers # i.e outside range of99.73% values outliers = [data_point for data_point,  z_score in zip(dataset, z_scores) if z_score>3] print(f'
Odľahlé hodnoty v súbore údajov sú {odľahlé hodnoty}')>

Výkon:

Z-Skóre: [-0,7574907 -0,59097335 -0,20243286 0,35262498 0,6301539 -0,72973781
-0,70198492 -0,00816262 0,13060185 0,54689523 1,10195307 3,32218443
-0,67423202 -0,64647913 -0,61872624 -0,59097335 -0,56322046]
Odľahlé hodnoty v súbore údajov sú [150]

Aplikácia Z-skóre

Z-skóre sa často používajú na škálovanie funkcií, aby sa rôzne funkcie dostali do spoločnej mierky. Funkcie normalizácie zaisťujú, že majú nulový priemer a rozptyl jednotiek, čo môže byť prospešné pre určité algoritmy strojového učenia, najmä tie, ktoré sa spoliehajú na merania vzdialenosti.
Z-skóre možno použiť na identifikáciu odľahlých hodnôt v súbore údajov. Dátové body so Z-skóre nad určitým prahom (zvyčajne 3 štandardné odchýlky od priemeru) možno považovať za odľahlé hodnoty.
Z-skóre možno použiť v algoritmoch detekcie anomálií na identifikáciu prípadov, ktoré sa výrazne odchyľujú od očakávaného správania.
Z-skóre možno použiť na transformáciu skreslených rozdelení na normálnejšie rozdelenia.
Pri práci s regresnými modelmi je možné analyzovať Z-skóre rezíduí na kontrolu homoskedasticity (konštantný rozptyl rezíduí).
Z-skóre je možné použiť pri škálovaní funkcií pri pohľade na ich štandardné odchýlky od priemeru.

Z-skóre vs. štandardná odchýlka

Z- skóre	Štandardná odchýlka
Transformujte nespracované údaje na štandardizovanú škálu.	Meria množstvo variácií alebo rozptylu v súbore hodnôt.
Uľahčuje porovnávanie hodnôt z rôznych súborov údajov, pretože odoberajú pôvodné merné jednotky.	Štandardná odchýlka zachováva pôvodné jednotky merania, takže je menej vhodná na priame porovnávanie medzi súbormi údajov s rôznymi jednotkami. pár c++
Uveďte, ako ďaleko je dátový bod od priemeru z hľadiska štandardných odchýlok, čím získate mieru relatívnej pozície dátového bodu v rámci rozdelenia	Vyjadrené v rovnakých jednotkách ako pôvodné údaje, poskytujúce absolútnu mieru rozloženia hodnôt okolo priemeru

Z- skóre

Štandardná odchýlka

Transformujte nespracované údaje na štandardizovanú škálu.

Meria množstvo variácií alebo rozptylu v súbore hodnôt.

Uľahčuje porovnávanie hodnôt z rôznych súborov údajov, pretože odoberajú pôvodné merné jednotky.

Štandardná odchýlka zachováva pôvodné jednotky merania, takže je menej vhodná na priame porovnávanie medzi súbormi údajov s rôznymi jednotkami.

pár c++

Uveďte, ako ďaleko je dátový bod od priemeru z hľadiska štandardných odchýlok, čím získate mieru relatívnej pozície dátového bodu v rámci rozdelenia

Vyjadrené v rovnakých jednotkách ako pôvodné údaje, poskytujúce absolútnu mieru rozloženia hodnôt okolo priemeru

Skontrolujte: Tabuľka Z-skóre

Prečo sa Z-skóre nazývajú štandardné skóre?

Z-skóre sú známe aj ako štandardné skóre, pretože štandardizujú hodnotu náhodnej premennej. To znamená, že zoznam štandardizovaných skóre má priemer 0 a štandardnú odchýlku 1,0. Z-skóre tiež umožňujú porovnanie skóre rôznych druhov premenných. Je to preto, že používajú relatívne postavenie na porovnávanie skóre z rôznych premenných alebo distribúcií.

Z-skóre sa často používa na porovnanie premennej so štandardným normálnym rozdelením (s μ = 0 a σ = 1).