Termín Zapamätanie pochádza z latinského slova memorandum ( zapamätať si ), čo sa v americkej angličtine bežne skracuje na memo a čo znamená transformovať výsledky funkcie na niečo, čo si treba zapamätať.
Vo výpočtovej technike sa memoizácia používa na urýchlenie počítačových programov odstránením opakovaného výpočtu výsledkov a tým, že sa zabráni opakovaným volaniam funkcií, ktoré spracúvajú rovnaký vstup.

Čo je zapamätanie
Obsah
- Čo je memoizácia?
- Prečo sa používa Memoization>
- Kde použiť Memoization?
- Typy zapamätania
- Ako sa technika zapamätania používa v dynamickom programovaní?
- Ako sa memoizácia líši od tabuľovania?
- Problémy z praxe kódovania na zapamätanie
- často kladené otázky
- 1) Je memorovanie lepšie ako DP?
- 2) Je ukladanie do pamäte rovnaké ako ukladanie do vyrovnávacej pamäte?
- 3) Prečo je memorovanie zhora nadol?
- 4) Používa sa na zapamätanie rekurzia?
- 5) Mal by som použiť tabuláciu alebo memoizáciu?
- 6) Kde sa používa memoizácia?
- 7) Prečo sa to nazýva memoizácia?
- 8) Ako memoizácia znižuje časovú zložitosť?
- 9) Aký je rozdiel medzi ukladaním do pamäte a ukladaním do vyrovnávacej pamäte?
- 10) Prečo je tabuľovanie rýchlejšie ako memoovanie?
- Záver
Prečo sa používa memoizácia?
Zapamätanie je špecifická forma ukladanie do vyrovnávacej pamäte ktorý sa používa v dynamické programovanie . Účelom ukladania do vyrovnávacej pamäte je zlepšiť výkon našich programov a zachovať prístup k údajom, ktoré možno použiť neskôr. V podstate ukladá predtým vypočítaný výsledok čiastkového problému a používa uložený výsledok pre rovnaký čiastkový problém. Tým sa odstráni mimoriadna námaha pri opakovanom počítaní toho istého problému. A už vieme, že ak sa rovnaký problém objaví znova a znova, potom je tento problém rekurzívny.
Kde použiť Memoization?
Môžeme použiť techniku memoizácie, kde sa použitie predtým vypočítaných výsledkov prichádza do obrazu. Tento druh problému sa väčšinou používa v kontexte rekurzia , najmä s problémami, ktoré zahŕňajú prekrývajúce sa čiastkové problémy .
Zoberme si príklad, keď sa rovnaký podproblém opakuje znova a znova.
Príklad, ktorý ukazuje, kde použiť memorovanie:
Let us try to find the factorial of a number .>
Nižšie je a rekurzívna metóda na nájdenie faktoriálu čísla:
int faktoriál (bez znamienka int n)
{
ak (n == 0)
návrat 1;
návrat n * faktoriál(n – 1);
}
Čo sa stane, ak použijeme túto rekurzívnu metódu?
Ak napíšete úplný kód pre vyššie uvedený úryvok, všimnete si, že v kóde budú 2 metódy:
1. factorial(n) 2. main()>
Teraz, ak máme viacero dotazov na nájdenie faktoriálu, ako napríklad hľadanie faktoriálu 2, 3, 9 a 5, potom budeme musieť zavolať metódu faktoriál() 4-krát:
factorial(2) factorial(3) factorial(9) factorial(5)>
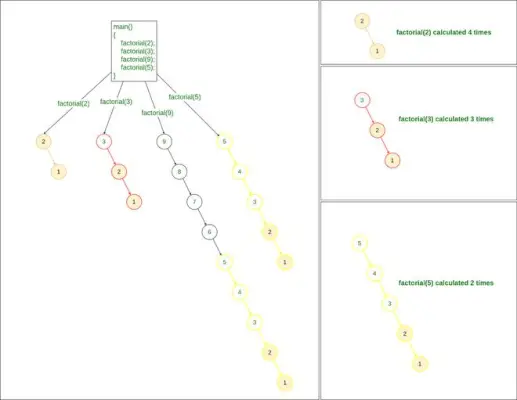
Rekurzívna metóda na nájdenie faktoriálu
Dá sa teda s istotou povedať, že na nájdenie faktoriálu čísel K čísel bude potrebná časová zložitosť O(N*K)
- O(N) nájsť faktoriál konkrétneho čísla a
- ŠÍPKA) na volanie metódy faktorial() K rôzne časy.
Ako môže memoizácia pomôcť pri takýchto problémoch?
Ak si všimneme vo vyššie uvedenom probléme, pri výpočte faktoriálu 9:
funkcia prototypu c++
- Počítame faktoriál 2
- Tiež počítame faktoriál 3,
- a Počítame aj faktoriál 5
Ak teda uložíme výsledok každého jednotlivého faktoriálu pri prvom výpočte, môžeme ľahko vrátiť faktoriál ľubovoľného požadovaného čísla len v čase O(1). Tento proces je známy ako Zapamätanie .
Riešenie pomocou zapamätania (Ako funguje zapamätanie?):
Ak najskôr nájdeme faktoriál 9 a uložíme výsledky jednotlivých čiastkových úloh, ľahko vytlačíme faktoriál každého vstupu v O(1).
Preto bude časová zložitosť pri hľadaní faktoriálových čísel pomocou memoizácie O(N)
- O(N) nájsť faktoriál najväčšieho vstupu
- O(1) na vytlačenie faktoriálu každého vstupu.
Typy zapamätania
Implementácia memoizácie závisí od meniacich sa parametrov, ktoré sú zodpovedné za riešenie problému. Existujú rôzne dimenzie ukladania do vyrovnávacej pamäte, ktoré sa používajú v technike zapamätania, nižšie sú niektoré z nich:
- 1D zapamätanie: Rekurzívna funkcia, ktorá má len jeden argument, ktorého hodnota nebola konštantná po každom volaní funkcie.
- 2D memorovanie: Rekurzívna funkcia, ktorá má iba dva argumenty, ktorých hodnota nebola konštantná po každom volaní funkcie.
- 3D memorovanie : Rekurzívna funkcia, ktorá má iba tri argumenty, ktorých hodnoty neboli konštantné po každom volaní funkcie.
Ako sa technika memoizácie používa v dynamickom programovaní?
Dynamické programovanie pomáha efektívne riešiť problémy, ktoré majú prekrývajúce sa podproblémy a optimálne vlastnosti podštruktúry. Myšlienkou dynamického programovania je rozdeliť problém na menšie čiastkové problémy a uložiť výsledok pre budúce použitie, čím sa eliminuje potreba opakovane počítať výsledok.
Existujú dva prístupy k formulácii riešenia dynamického programovania:
- Prístup zhora nadol: Tento prístup sa riadi zapamätanie technika . Skladá sa to z rekurzia a ukladanie do vyrovnávacej pamäte . Vo výpočte predstavuje rekurzia proces opakovaného volania funkcií, zatiaľ čo vyrovnávacia pamäť sa týka procesu ukladania medzivýsledkov.
- Prístup zdola nahor: Tento prístup využíva tabelácia technika implementovať riešenie dynamického programovania. Rieši rovnaké problémy ako predtým, ale bez rekurzie. V tomto prístupe iterácia nahrádza rekurziu. Preto nedochádza k chybe pretečenia zásobníka alebo réžii rekurzívnych procedúr.
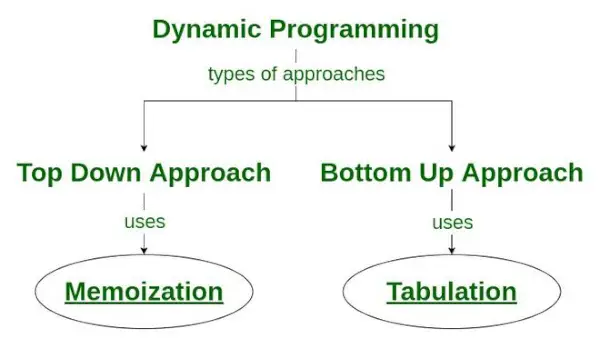
Ako sa technika memoizácie používa v dynamickom programovaní
Ako sa memoizácia líši od tabuľovania?

Tabuľka verzus memorizácia
Ďalšie podrobnosti nájdete na: Tabuľka verzus memoizácia
Problémy s nácvikom kódovania pri memoizácii
| Otázka | Článok | Prax | Video |
|---|---|---|---|
| Spočítajte spôsoby, ako sa dostať na n'-tý schod | vyhliadka | Vyriešiť | Sledujte |
| Problém prerušenia slov | DP-32 | vyhliadka | Vyriešiť | Sledujte |
| Program pre Fibonacciho čísla | vyhliadka | Vyriešiť | Sledujte |
| n-té katalánske číslo | vyhliadka | Vyriešiť | Sledujte |
| Problém zlatej bane | vyhliadka | Vyriešiť | Sledujte |
| Problém podmnožiny súčtu | vyhliadka | Riešiť | Sledujte |
| Rezanie tyče | vyhliadka | Vyriešiť | Sledujte |
| Cesta minimálnych nákladov | vyhliadka | Vyriešiť | Sledujte |
| Minimálny počet skokov na dosiahnutie konca | vyhliadka | Vyriešiť | Sledujte |
| Najdlhší palindromický podreťazec | Set 1 | vyhliadka | Vyriešiť | Sledujte |
| Najdlhšia opakovaná sekvencia | vyhliadka | Vyriešiť | Sledujte |
| Spočítajte spôsoby, ako sa dostať na n-tý schodík pomocou kroku 1, 2 alebo 3 | vyhliadka | Vyriešiť | Sledujte |
| Spočítajte rôzne spôsoby vyjadrenia N ako súčtu 1, 3 a 4 | vyhliadka | Vyriešiť | Sledujte |
| Spočítajte počet spôsobov, ako prekonať vzdialenosť | vyhliadka | Vyriešiť | Sledujte |
| Počet polí, ktoré majú po sebe idúci prvok s rôznymi hodnotami | vyhliadka | Vyriešiť | Sledujte |
| Súvislé podpole s najväčšou sumou | vyhliadka | Vyriešiť | Sledujte |
| Súvislé podpole s najmenším súčtom | vyhliadka | Riešiť | Sledujte |
| Jedinečné cesty v mriežke s prekážkami | vyhliadka | Vyriešiť | Sledujte |
| Rôzne spôsoby sčítania n pomocou čísel väčších alebo rovných m 10 ml v oz | vyhliadka | Vyriešiť | Sledujte |
Často kladené otázky (FAQ) o memoizácii
1: Je memorovanie lepšie ako DP?
Memoizácia je prístup zhora nadol k riešeniu problému s dynamickým programovaním. Nazýva sa to memoizácia, pretože vytvoríme poznámku pre hodnoty vrátené z riešenia každého problému.
2: Je ukladanie do pamäte rovnaké ako ukladanie do vyrovnávacej pamäte?
Memoizácia je vlastne špecifický typ ukladania do vyrovnávacej pamäte. Pojem ukladanie do vyrovnávacej pamäte sa môže vo všeobecnosti vzťahovať na akúkoľvek techniku ukladania (ako je ukladanie do vyrovnávacej pamäte HTTP) na budúce použitie, ale ukladanie do pamäte sa konkrétnejšie vzťahuje na funkciu ukladania do vyrovnávacej pamäte, ktorá vracia hodnotu.
3: Prečo je memorovanie zhora nadol?
Prístup zhora nadol rozdeľuje veľký problém na viacero podproblémov. ak je už podproblém vyriešený, znova použite odpoveď. V opačnom prípade vyriešte podproblém a uložte výsledok do nejakej pamäte.
4: Používa sa na zapamätanie rekurzia?
Memorizácia sa riadi prístupom zhora nadol k riešeniu problému. Pozostáva z rekurzie a ukladania do vyrovnávacej pamäte. Vo výpočte predstavuje rekurzia proces opakovaného volania funkcií, zatiaľ čo vyrovnávacia pamäť sa týka procesu ukladania medzivýsledkov.
5: Mal by som použiť tabuláciu alebo memoizáciu?
Pri problémoch, ktoré si vyžadujú vyriešenie všetkých čiastkových problémov, tabuľka zvyčajne prevyšuje memorovanie konštantným faktorom. Je to preto, že tabuľka nemá žiadnu réžiu rekurzie, čo znižuje čas na vyriešenie zásobníka volaní rekurzie z pamäte zásobníka.
Vždy, keď je potrebné vyriešiť podproblém pre pôvodný problém, uprednostňuje sa zapamätanie, pretože podproblém sa rieši lenivo, t. j. vykonajú sa len potrebné výpočty.
6: Kde sa používa memoizácia?
Memoizácia je optimalizačná technika používaná na zrýchlenie počítačových programov ukladaním výsledkov drahých funkčných volaní do vyrovnávacej pamäte a ich vrátením, keď sa znova objavia rovnaké vstupy.
7: Prečo sa to nazýva memoizácia?
Pojem memoizácia pochádza z latinského slova memorandum (zapamätať si), ktoré sa v americkej angličtine bežne skracuje na memo a znamená transformovať výsledky funkcie na niečo, čo si treba zapamätať.
8: Ako memorovanie znižuje časovú zložitosť?
Riešenie toho istého problému znova a znova si vyžaduje čas a zvyšuje zložitosť celého programu za chodu. Tento problém sa dá vyriešiť udržiavaním určitej vyrovnávacej pamäte alebo pamäte, kde uložíme už vypočítaný výsledok problému pre určitý konkrétny vstup. Ak teda nechceme prepočítavať rovnaký problém, môžeme jednoducho použiť výsledok uložený v pamäti a znížiť tak časovú zložitosť.
9: Aký je rozdiel medzi ukladaním do pamäte a ukladaním do vyrovnávacej pamäte?
Zapamätanie je v skutočnosti špecifický typ ukladania do vyrovnávacej pamäte, ktorý zahŕňa ukladanie návratovej hodnoty funkcie do vyrovnávacej pamäte na základe vstupu. Ukladanie do vyrovnávacej pamäte je všeobecnejší pojem. Napríklad ukladanie do vyrovnávacej pamäte HTTP je ukladanie do vyrovnávacej pamäte, ale nie je to ukladanie do pamäte.
10: Prečo je tabuľovanie rýchlejšie ako memorovanie?
Tabulácia je zvyčajne rýchlejšia ako memoizácia, pretože je iteratívna a riešenie podproblémov nevyžaduje réžiu rekurzívnych volaní.
Memoizácia je technika používaná v informatike na urýchlenie vykonávania rekurzívnych alebo výpočtovo nákladných funkcií ukladaním výsledkov volaní funkcií do vyrovnávacej pamäte a vrátením výsledkov uložených do vyrovnávacej pamäte, keď sa znova vyskytnú rovnaké vstupy.
Základnou myšlienkou memoizácie je uložiť výstup funkcie pre danú množinu vstupov a vrátiť výsledok uložený vo vyrovnávacej pamäti, ak sa funkcia znova zavolá s rovnakými vstupmi. Táto technika môže ušetriť výpočtový čas, najmä pre funkcie, ktoré sa volajú často alebo majú vysokú časovú zložitosť.
Tu je podrobný návod na implementáciu memorovania:
Identifikujte funkciu, ktorú chcete optimalizovať pomocou ukladania do pamäte. Táto funkcia by mala mať opakované a drahé výpočty pre rovnaký vstup.
Vytvorte objekt slovníka na uloženie výsledkov funkcie uložených vo vyrovnávacej pamäti. Kľúče slovníka by mali byť vstupnými parametrami funkcie a hodnotami by mali byť vypočítané výsledky.
Na začiatku funkcie skontrolujte, či sú vstupné parametre už prítomné v slovníku vyrovnávacej pamäte. Ak sú, vráťte výsledok uložený vo vyrovnávacej pamäti.
Ak vstupné parametre nie sú v slovníku vyrovnávacej pamäte, vypočítajte výsledok a uložte ho do slovníka vyrovnávacej pamäte so vstupnými parametrami ako kľúčom.
Vráťte vypočítaný výsledok.
Tu je príklad kódu Python na implementáciu memoizácie pomocou slovníka:
Python3
def> fibonacci(n, cache>=>{}):> >if> n>in> cache:> >return> cache[n]> >if> n>=>=> 0>:> >result>=> 0> >elif> n>=>=> 1>:> >result>=> 1> >else>:> >result>=> fibonacci(n>->1>)>+> fibonacci(n>->2>)> >cache[n]>=> result> >return> result> |
>
>Výkon
>
Vo vyššie uvedenom kóde definujeme funkciu nazývanú Fibonacci, ktorá vypočíta n-té číslo vo Fibonacciho postupnosti. Na ukladanie výsledkov volaní funkcií používame objekt slovníka s názvom cache. Ak sa vstupný parameter n už nachádza v slovníku vyrovnávacej pamäte, vrátime výsledok uložený vo vyrovnávacej pamäti. V opačnom prípade výsledok vypočítame pomocou rekurzívnych volaní Fibonacciho funkcie a pred vrátením ho uložíme do vyrovnávacieho slovníka.
Zapamätanie možno použiť na optimalizáciu výkonu mnohých funkcií, ktoré majú opakované a drahé výpočty. Uložením výsledkov volaní funkcií do vyrovnávacej pamäte sa môžeme vyhnúť zbytočným výpočtom a urýchliť vykonávanie funkcie.
Záver
Memoizácia je koncept programovania a možno ho použiť v akomkoľvek programovacom jazyku. Jeho absolútnym cieľom je optimalizácia programu. Tento problém sa zvyčajne vyskytuje, keď programy vykonávajú náročné výpočty. Táto technika ukladá všetky predchádzajúce vypočítané výsledky do vyrovnávacej pamäte, takže sa nebude musieť prepočítavať pre rovnaký problém.
Súvisiace články:
- Zapamätanie pomocou dekoratérov v Pythone
- Zapamätanie JavaScriptu
