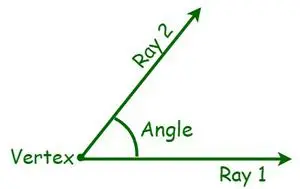
V geometrii je uhol základným meraním geometrického tvaru. Uhol je definovaný ako stupeň rotácie okolo priesečníka dvoch línií alebo rovín, ktoré sú potrebné na to, aby jedna bola v súlade s druhou. Existujú rôzne druhy uhlov na základe merania uhla. Meria sa v stupňoch alebo radiánoch. Uhol je tvar tvorený dvoma čiarami alebo lúčmi, ktoré sa odchyľujú od spoločného bodu nazývaného vrchol. Keď sa pretínajú dva lúče, t.j. keď sa polpriamky premietajú so spoločným koncovým bodom, vytvorí sa uhol. Teraz sa spoločné koncové body nazývajú vrcholy, zatiaľ čo lúče sú známe ako ramená.
Typy uhlov

- Ostrý uhol: Ostrý uhol je uhol, ktorý je väčší ako 0 stupňov a menší ako 90 stupňov, t. j. má rozsah od 0° do 90° (oba s výnimkou).
- Pravý uhol: Pravý uhol sa označuje ako uhol, ktorý meria presne 90 stupňov.
- Tupý uhol: Tupý uhol je uhol, ktorý je väčší ako 90 stupňov a menší ako 180 stupňov, t. j. je v rozsahu od 90° do 180° (oba s výnimkou).
- Priamy uhol: Priamy uhol sa označuje ako uhol, ktorý meria presne 180 stupňov.
- Uhol odrazu: Uhol odrazu je uhol, ktorý je väčší ako 180 stupňov a menší ako 360 stupňov, t. j. je v rozsahu od 180° do 360° (oba exkluzívne).
- Úplný uhol alebo úplná rotácia: Úplný uhol sa označuje ako uhol, ktorý meria presne 360 stupňov.
Existujú aj iné typy uhlov, ako sú doplnkové uhly, doplnkové uhly a susedné a nesusediace uhly.
- Doplnkové uhly: Dva uhly sa považujú za komplementárne, ak ich súčet je pravý uhol, t. j. 90°.
- Doplnkové uhly: Dva uhly sa považujú za doplnkové, ak sa ich súčet rovná 180°.
- Susedné uhly: Hovorí sa, že dva uhly susedia, ak zdieľajú spoločný vrchol a spoločné rameno.
- Nesusediace uhly: Dva uhly sa považujú za nesusediace, ak nezdieľajú spoločný vrchol a spoločné rameno.
Vzorec na hľadanie uhlov
Existujú rôzne typy vzorcov na nájdenie uhla; niektoré z nich sú vzorec stredného uhla, vzorec dvojitého uhla, vzorec polovičného uhla, vzorec zloženého uhla, vzorec vnútorného uhla atď.
- Na určenie uhla segmentu vytvoreného v kruhu používame vzorec stredného uhla.
- Na určenie chýbajúceho uhla v mnohouholníku používame súčet vzorca vnútorných uhlov.
- Na nájdenie chýbajúceho uhla pravouhlého trojuholníka používame trigonometrické pomery.
- Na nájdenie chýbajúceho uhla nepravoúhlého trojuholníka používame sínusový alebo kosínusový zákon.
Názov vzorca | Vzorec | Ako nájsť neznámy uhol? |
|---|---|---|
| Vzorec centrálneho uhla | 0 = (s x 360°)/2prTu je s dĺžka oblúka a r polomer kruhu | Nahradením hodnôt dĺžky oblúka a polomeru kruhu určíte uhol segmentu vytvoreného v kruhu. |
| Vzorec súčtu vnútorných uhlov | 180°(n-2)Tu je n počet strán mnohouholníka | Ak chcete určiť neznámy vnútorný uhol mnohouholníka, najprv vypočítajte súčet všetkých vnútorných uhlov pomocou tohto vzorca a potom od výsledku odčítajte súčet všetkých známych uhlov. |
| Trigonometrické pomery | sin θ = opačná strana/hypotenzacos θ = susedná strana/hypotenzatan θ = opačná strana/susedná strana | V závislosti od dostupných dvoch strán pravouhlého trojuholníka vyberte jeden z týchto trigonometrických pomerov, aby ste našli neznámy uhol. |
| Sinesov zákon | a/sin A = b/sin B = c/sin CTu sú A, B a C vnútorné uhly trojuholníka a a, b a c sú ich príslušné protiľahlé strany. | Keď poznáme dve strany a nezahrnutý uhol (alebo) dva uhly a nezaradenú stranu, potom možno na určenie neznámych uhlov trojuholníka použiť zákon sínusov. |
| Zákon kosínusov | a2= b2+ c2– 2 bc čos Ab2= c2+ a2– 2 ca ako Bc2= a2+ b2– 2ab čos CTu sú A, B a C vnútorné uhly trojuholníka a a, b a c sú ich príslušné protiľahlé strany. | Keď poznáme tri strany (alebo) dve strany a uzavretý uhol, potom sa na určenie neznámych uhlov trojuholníka dá použiť zákon kosínusov. |
Vzorové otázky
Otázka 1: Nájdite uhol vo vrchole B daného trojuholníka pomocou niektorého z goniometrických vzorcov na hľadanie uhlov.

python triedená n-tica
Riešenie:
Vzhľadom na to,
BC = 3 jednotky = susediaca strana θ.
uložiť video z youtube vlcAC = 4 jednotky = opačná strana θ.
V tomto prípade poznáme opačnú aj susednú stranu θ. Preto môžeme použiť vzorec dotyčnice na nájdenie θ.
⇒ tan θ = opačná strana/susedná strana
⇒ tan θ = 4/3
⇒ θ = tan-1(4/3) ⇒ 6 = 53,1°
Uhol vo vrchole B je teda 53,1°.
Otázka 2: Nájdite uhly vo vrcholoch X a Y, ak ∠Z = 35° a x = 3 palce, y = 8 palcov az = 3,5 palca.

Riešenie:
Vzhľadom na to,
∠Z = 35° a x = 6 palcov, y = 3 palce a z = 3,5 palca
Keďže poznáme všetky tri strany a uhol, môžeme použiť vzorec sínusového pravidla.
Zo vzorca sínusového pravidla máme
x/sin X = y/sin Y = z/sin Z
teraz
y/sin Y = z/sin Z
⇒ 3/sin Y = 3,5/sin 35°
⇒ 3/bez Y = 3,5/0,574 {Sin 35° = 0,574}
⇒ sin Y = 3 × (0,574/3,5) = 0,492
⇒ ∠Y = hriech−1(0,492) = 29,47°
Vieme, že súčet troch uhlov v trojuholníku je 180°.
⇒ ∠X + ∠Y + ∠Z = 180°
⇒ ∠X + 29,47° + 35° = 180°
⇒ ∠X = 180° – 64,47° = 115,53°
Preto ∠X = 115,53° a ∠Y = 29,47°.
Otázka 3: Vypočítajte piaty vnútorný uhol päťuholníka, ak štyri z jeho vnútorných uhlov sú 110°, 85°, 136° a 105°.
Riešenie:
Počet strán päťuholníka (n) = 5.
Teraz súčet všetkých 5 vnútorných uhlov päťuholníka = 180 (n -2)°
= 180 (5 – 2)° = 540°.
Súčet daných 4 vnútorných uhlov = 110°+ 85°+ 136°+ a 105°= 436°.
Takže piaty vnútorný uhol = 540° – 436° = 104°
Piaty vnútorný uhol päťuholníka je teda 104°.
Otázka 4: Určte hodnotu y a tiež mieru uhlov na danom obrázku.

puzdro java switch
Riešenie:
Z uvedeného obrázku môžeme vidieť, že (4y – 6)° a (3y + 5)° sú komplementárne uhly, t.j. súčet (4y – 6)° a (3y + 5)° je 90 °.
⇒ (4r – 6)° + (3r + 5)° = 90°
⇒ (7r – 1)° = 90°
⇒ 7y = 90° + 1° = 91°
⇒ y = 91°/7 = 13°
Teraz, (4r – 6)° = (4 × 13 – 6)° = (52 – 6)° = 46°
(3r + 5)° = (3 × 13 + 5)° = (39 + 5)° = 44°
Otázka 5: Nájdite uhol vo vrchole Q v danom trojuholníku pomocou jedného zo vzorcov na hľadanie uhlov.

Riešenie:
Dané, p = QR = 6 cm, q = PR = 9 cm a r = PQ = 7 cm.
Keďže poznáme všetky tri strany a uhol, môžeme použiť vzorec kosínusového pravidla na nájdenie vrcholu uhla Q.
⇒ q2= p2+ r2– 2pr čos Q
⇒ 92= 62+ 72– 2 (6) (7) cos Q
⇒ 81 = 36 + 49 – 84 cos Q
⇒ 81 = 85 – 84cos Q
⇒84 cos Q = 81 – 85
⇒ 84 cos Q = -4
⇒ cos Q = -4/84 = -1/21
⇒ ∠Q = cos-1(-1/21) = 92,72°
Preto uhol vo vrchole Q, ∠Q = 92,72°.
Otázka 6: Vypočítajte uhol segmentu vytvoreného v kruhu, ak je dĺžka oblúka 12π a polomer je 9 cm.
Riešenie:
aws sns
Vzhľadom na to,
Dĺžka oblúka = 12π
Polomer (r) = 9 cm
Teraz vzorec uhla je:
⇒ θ = (s×360°)/2pr
⇒ θ = (12π × 360°)/(2π × 5)
⇒ 0 = 12 x 360°/10
⇒ 6 = 240°
Uhol je teda 240°.
