Topologické triedenie pre Riadený acyklický graf (DAG) je lineárne usporiadanie vrcholov také, že pre každú smerovanú hranu u-v je vrchol v prichádza skôr v v objednávke.
Poznámka: Topologické triedenie pre graf nie je možné, ak graf nie je a DAY .
Príklad:
Odporúčaná praxRiešenie založené na DFS na nájdenie topologického triedenia už sa diskutovalo.Vstup: Graf :
funkcie java 8Príklad
Výkon: 5 4 2 3 1 0
Vysvetlenie: Prvý vrchol v topologickom triedení je vždy vrchol s in-stupňom 0 (vrchol bez prichádzajúcich hrán). Topologické triedenie nasledujúceho grafu je 5 4 2 3 1 0. Pre graf môže existovať viac ako jedno topologické triedenie. Ďalšie topologické triedenie nasledujúceho grafu je 4 5 2 3 1 0.
Topologické poradie nemusí byť jedinečné:
Topologické triedenie je problém závislosti, v ktorom dokončenie jednej úlohy závisí od dokončenia niekoľkých ďalších úloh, ktorých poradie sa môže meniť. Poďme pochopiť tento koncept na príklade:
Predpokladajme, že našou úlohou je dostať sa do našej školy a aby sme sa tam dostali, musíme sa najprv obliecť. Závislosti na nosení oblečenia sú zobrazené v nižšie uvedenom grafe závislostí. Napríklad nemôžete nosiť topánky pred nosením ponožiek.
Z vyššie uvedeného obrázku by ste si už uvedomili, že existuje viacero spôsobov, ako sa obliecť, obrázok nižšie ukazuje niektoré z týchto spôsobov.
Môžete uviesť všetky možné topologické usporiadanie obliekania pre vyššie uvedený graf závislosti?
mapy java
Algoritmus pre topologické triedenie pomocou DFS:
Tu je krok za krokom algoritmus pre topologické triedenie pomocou hĺbkového prvého vyhľadávania (DFS):
- Vytvorte graf s n vrcholy a m - orientované hrany.
- Inicializujte zásobník a navštívené pole veľkosti n .
- Pre každý nenavštívený vrchol v grafe vykonajte nasledovné:
- Zavolajte funkciu DFS s vrcholom ako parametrom.
- Vo funkcii DFS označte vrchol ako navštívený a rekurzívne zavolajte funkciu DFS pre všetkých nenavštívených susedov vrcholu.
- Po návšteve všetkých susedov zatlačte vrchol na zásobník.
- Koniec koncov, vrcholy boli navštívené, vyberte prvky zo zásobníka a pridajte ich do zoznamu výstupov, kým zásobník nebude prázdny.
- Výsledný zoznam je topologicky zoradené poradie grafu.
Ilustrácia Algoritmus topologického triedenia:
Nižšie uvedený obrázok je ilustráciou vyššie uvedeného prístupu:

Celkový pracovný postup topologického triedenia
Krok 1:
- Spustíme DFS z uzla 0, pretože má nulové prichádzajúce uzly
- Zatlačíme uzol 0 do zásobníka a presunieme sa na ďalší uzol s minimálnym počtom susedných uzlov, tj uzol 1.
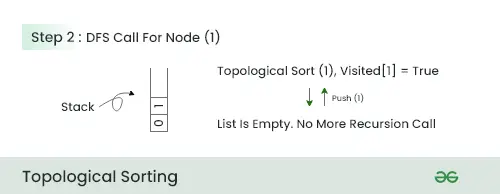
Krok 2:
- V tomto kroku, pretože neexistuje žiadny susedný uzol, zatlačte uzol 1 v zásobníku a presuňte sa na ďalší uzol.
Krok 3:
- V tomto kroku zvolíme uzol 2, pretože má minimálny počet susedných uzlov po 0 a 1.
- Zavoláme DFS pre uzol 2 a posunieme všetky uzly, ktoré prichádzajú z uzla 2 v opačnom poradí.
- Takže stlačte 3 a potom stlačte 2 .
Krok 4:
- Teraz voláme DFS pre uzol 4
- Pretože 0 a 1 už sú v zásobníku, tak len zatlačíme uzol 4 v zásobníku a vrátime sa.
Krok 5:
- V tomto kroku, pretože všetky susedné uzly 5 sú už v zásobníku, zatlačíme uzol 5 do zásobníka a vrátime sa.
Krok 6: Toto je posledný krok topologického triedenia, v ktorom vyberieme všetky prvky zo zásobníka a vytlačíme ich v tomto poradí.
Nižšie je uvedená implementácia vyššie uvedeného prístupu:
C++ #include using namespace std; // Function to perform DFS and topological sorting void topologicalSortUtil(int v, vector>& adj, vektor & navštívil, zásobník & Stack) { // Označenie aktuálneho uzla ako navštíveného[v] = true; // Opakuje sa pre všetky susedné vrcholy pre (int i : adj[v]) { if (!navštívené[i]) topologicalSortUtil(i, adj, visited, Stack); } // Vloží aktuálny vrchol do zásobníka, ktorý uloží výsledok Stack.push(v); } // Funkcia na vykonanie topologického triedenia void topologicalSort(vector>& adj, int V) { zásobník Stoh; // Stack na uloženie výsledného vektora navštívil(V, nepravda); // Volanie rekurzívnej pomocnej funkcie na uloženie // Topologické zoradenie začínajúce od všetkých vrcholov jeden po // jeden pre (int i = 0; i< V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, Stack); } // Print contents of stack while (!Stack.empty()) { cout << Stack.top() << ' '; Stack.pop(); } } int main() { // Number of nodes int V = 4; // Edges vector> hrany = { { 0, 1 }, { 1, 2 }, { 3, 1 }, { 3, 2 } }; // Graf reprezentovaný ako vektor zoznamu susedstva> adj(V); for (auto i : hrany) { adj[i[0]].push_back(i[1]); } cout<< 'Topological sorting of the graph: '; topologicalSort(adj, V); return 0; }>
Java import java.util.*; public class TopologicalSort { // Function to perform DFS and topological sorting static void topologicalSortUtil(int v, List> adj, boolean[] navštívené, zásobník stack) { // Označenie aktuálneho uzla ako navštíveného[v] = true; // Opakuje sa pre všetky susedné vrcholy pre (int i : adj.get(v)) { if (!navštívené[i]) topologicalSortUtil(i, adj, visited, stack); } // Vloží aktuálny vrchol do zásobníka, ktorý uloží // výsledok stack.push(v); } // Funkcia na vykonanie topologického triedenia static void topologicalSort(List> adj, int V) { // Zásobník na uloženie výsledku Zásobník zásobník = nový zásobník (); boolean[] navštívené = new boolean[V]; // Volanie rekurzívnej pomocnej funkcie na uloženie // Topologické triedenie začínajúce od všetkých vrcholov po jednom // po jednom pre (int i = 0; i< V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Print contents of stack System.out.print( 'Topological sorting of the graph: '); while (!stack.empty()) { System.out.print(stack.pop() + ' '); } } // Driver code public static void main(String[] args) { // Number of nodes int V = 4; // Edges List> hrany = new ArrayList(); edge.add(Arrays.asList(0, 1)); edge.add(Arrays.asList(1, 2)); edge.add(Arrays.asList(3, 1)); edge.add(Arrays.asList(3, 2)); // Graf reprezentovaný ako zoznam susediacich zoznamov> adj = new ArrayList(V); pre (int i = 0; i< V; i++) { adj.add(new ArrayList()); } for (List i : hrany) { adj.get(i.get(0)).add(i.get(1)); } topologicalSort(adj, V); } }>
Python3 def topologicalSortUtil(v, adj, visited, stack): # Mark the current node as visited visited[v] = True # Recur for all adjacent vertices for i in adj[v]: if not visited[i]: topologicalSortUtil(i, adj, visited, stack) # Push current vertex to stack which stores the result stack.append(v) # Function to perform Topological Sort def topologicalSort(adj, V): # Stack to store the result stack = [] visited = [False] * V # Call the recursive helper function to store # Topological Sort starting from all vertices one by # one for i in range(V): if not visited[i]: topologicalSortUtil(i, adj, visited, stack) # Print contents of stack print('Topological sorting of the graph:', end=' ') while stack: print(stack.pop(), end=' ') # Driver code if __name__ == '__main__': # Number of nodes V = 4 # Edges edges = [[0, 1], [1, 2], [3, 1], [3, 2]] # Graph represented as an adjacency list adj = [[] for _ in range(V)] for i in edges: adj[i[0]].append(i[1]) topologicalSort(adj, V)> C# using System; using System.Collections.Generic; class Program { // Function to perform DFS and topological sorting static void TopologicalSortUtil(int v, List> adj, bool[] navštívené, zásobník stack) { // Označenie aktuálneho uzla ako navštíveného[v] = true; // Opakuje sa pre všetky susedné vrcholy foreach(int i in adj[v]) { if (!navštívené[i]) TopologicalSortUtil(i, adj, visited, stack); } // Vloží aktuálny vrchol do zásobníka, v ktorom sa uloží // výsledok stack.Push(v); } // Funkcia na vykonanie statického topologického triedenia void TopologicalSort(List> adj, int V) { // Zásobník na uloženie výsledku Zásobník zásobník = nový zásobník (); bool[] navštívené = nový bool[V]; // Volanie rekurzívnej pomocnej funkcie na uloženie // Topologické triedenie začínajúce od všetkých vrcholov po jednom // po jednom pre (int i = 0; i< V; i++) { if (!visited[i]) TopologicalSortUtil(i, adj, visited, stack); } // Print contents of stack Console.Write('Topological sorting of the graph: '); while (stack.Count>0) { Console.Write(stack.Pop() + ' '); } } // Kód ovládača static void Main(string[] args) { // Počet uzlov int V = 4; // Zoznam okrajov> hrany = nový zoznam>{ nový zoznam { 0, 1 }, nový zoznam { 1, 2 }, nový zoznam { 3, 1 }, nový zoznam { 3, 2} }; // Graf reprezentovaný ako zoznam susediacich zoznamov> adj = nový zoznam>(); pre (int i = 0; i< V; i++) { adj.Add(new List ()); } foreach(Zoznam i v hranách) { adj[i[0]].Add(i[1]); } TopologicalSort(adj, V); } }>
Javascript // Function to perform DFS and topological sorting function topologicalSortUtil(v, adj, visited, stack) { // Mark the current node as visited visited[v] = true; // Recur for all adjacent vertices for (let i of adj[v]) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Push current vertex to stack which stores the result stack.push(v); } // Function to perform Topological Sort function topologicalSort(adj, V) { // Stack to store the result let stack = []; let visited = new Array(V).fill(false); // Call the recursive helper function to store // Topological Sort starting from all vertices one by // one for (let i = 0; i < V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Print contents of stack console.log('Topological sorting of the graph: '); while (stack.length>0) { console.log(stack.pop() + ' '); } } // Kód ovládača (() => { // Počet uzlov const V = 4; // Hrany const = [[0, 1], [1, 2], [3, 1], [3, 2]] // Graf reprezentovaný ako zoznam susedstva const adj = Array.from({ dĺžka: V }, () => [] for (nech i hrán) { adj[i[0]].push; (i[1] } topologicalSort(adj, V)();> Výkon
Topological sorting of the graph: 3 0 1 2>
Časová zložitosť: O(V+E). Vyššie uvedený algoritmus je jednoducho DFS s extra zásobníkom. Časová zložitosť je teda rovnaká ako DFS
Pomocný priestor: O(V). Ďalší priestor je potrebný pre zásobník
Topologické triedenie pomocou BFS:
operačné systémy macC++
#include #include #include using namespace std; // Class to represent a graph class Graph { int V; // No. of vertices list * adj; // Ukazovateľ na pole obsahujúce // zoznamy susedstva public: Graph(int V); // Konštruktor void addEdge(int v, int w); // Funkcia na pridanie hrany do grafu void topologicalSort(); // vypíše topologický druh // celého grafu }; Graph::Graph(int V) { this->V = V; adj = nový zoznam [V]; } void Graph::addEdge(int v, int w) { adj[v].push_back(w); // Pridajte w do zoznamu v. } // Funkcia na vykonanie topologického triedenia void Graph::topologicalSort() { // Vytvorenie vektora na uloženie vektora všetkých vrcholov v stupni in_degree(V, 0); // Prechádzajte zoznamami susedných miest na vyplnenie // vrcholov pre (int v = 0; v< V; ++v) { for (auto const& w : adj[v]) in_degree[w]++; } // Create a queue and enqueue all vertices with // in-degree 0 queue q; pre (int i = 0; i< V; ++i) { if (in_degree[i] == 0) q.push(i); } // Initialize count of visited vertices int count = 0; // Create a vector to store topological order vector top_order; // Jeden po druhom vyraďte vrcholy z frontu a fronty // susedné vrcholy, ak sa in-stupeň susedných stane 0 while (!q.empty()) { // Extrahujte predok fronty (alebo vykonajte vyradenie) // a pridajte ho do topologické poradie int u = q.front(); q.pop(); top_order.push_back(u); // Iterovať cez všetky jeho susedné uzly // vyradeného uzla u a znížiť ich stupeň // o 1 zoznam ::iterator itr; for (itr = adj[u].begin(); itr != adj[u].end(); ++itr) // Ak sa in-degree stane nulou, pridajte ho do frontu, ak (--in_degree[*itr ] == 0) q.push(*itr); počet++; } // Skontrolujte, či došlo k cyklu if (count != V) { cout<< 'Graph contains cycle
'; return; } // Print topological order for (int i : top_order) cout << i << ' '; } // Driver code int main() { // Create a graph given in the above diagram Graph g(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); cout << 'Following is a Topological Sort of the given ' 'graph
'; g.topologicalSort(); return 0; }> Java import java.util.ArrayList; import java.util.LinkedList; import java.util.Queue; // Class to represent a graph class Graph { private int V; // No. of vertices private ArrayList [] adj; // Zoznam susedstva // reprezentácia // grafu // Konštruktor Graph(int V) { this.V = V; adj = new ArrayList[V]; pre (int i = 0; i< V; ++i) adj[i] = new ArrayList(); } // Function to add an edge to the graph void addEdge(int v, int w) { adj[v].add(w); // Add w to v’s list. } // Function to perform Topological Sort void topologicalSort() { // Create an array to store in-degree of all // vertices int[] inDegree = new int[V]; // Calculate in-degree of each vertex for (int v = 0; v < V; ++v) { for (int w : adj[v]) { inDegree[w]++; } } // Create a queue and enqueue all vertices with // in-degree 0 Queue q = new LinkedList(); pre (int i = 0; i< V; ++i) { if (inDegree[i] == 0) q.add(i); } // Initialize count of visited vertices int count = 0; // Create an ArrayList to store topological order ArrayList topOrder = new ArrayList(); // Jeden po druhom vyraďte vrcholy z frontu a // zaraďte susedné vrcholy, ak sa in-stupeň // susedného stane 0, zatiaľ čo (!q.isEmpty()) { // Extrahujte predok frontu a pridajte ho do // topologického poradia int u = q.poll(); topOrder.add(u); počet++; // Iterujte cez všetky susedné uzly // vyradeného uzla u a znížte ich stupeň // o 1 for (int w : adj[u]) { // Ak sa in-degree stane nulou, pridajte ho do // frontu if (--inDegree[w] == 0) q.add(w); } } // Skontrolujte, či došlo k cyklu if (počet != V) { System.out.println('Graf obsahuje cyklus'); návrat; } // Tlač topologického poradia pre (int i : topOrder) System.out.print(i + ' '); } } // Kód ovládača public class Main { public static void main(String[] args) { // Vytvorenie grafu uvedeného vo vyššie uvedenom diagrame Graph g = new Graph(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); System.out.println( 'Nasleduje topologické zoradenie daného grafu'); g.topologicalSort(); } }> Python3 from collections import defaultdict class Graph: def __init__(self, vertices): # Number of vertices self.V = vertices # Dictionary to store adjacency lists self.adj = defaultdict(list) def addEdge(self, u, v): # Function to add an edge to the graph self.adj[u].append(v) def topologicalSort(self): # Function to perform Topological Sort # Create a list to store in-degree of all vertices in_degree = [0] * self.V # Traverse adjacency lists to fill in_degree of vertices for i in range(self.V): for j in self.adj[i]: in_degree[j] += 1 # Create a queue and enqueue all vertices with in-degree 0 q = [] for i in range(self.V): if in_degree[i] == 0: q.append(i) # Initialize count of visited vertices count = 0 # Create a list to store topological order top_order = [] # One by one dequeue vertices from queue and enqueue # adjacent vertices if in-degree of adjacent becomes 0 while q: # Extract front of queue (or perform dequeue) # and add it to topological order u = q.pop(0) top_order.append(u) # Iterate through all its neighbouring nodes # of dequeued node u and decrease their in-degree # by 1 for node in self.adj[u]: # If in-degree becomes zero, add it to queue in_degree[node] -= 1 if in_degree[node] == 0: q.append(node) count += 1 # Check if there was a cycle if count != self.V: print('Graph contains cycle') return # Print topological order print('Topological Sort:', top_order) # Driver code if __name__ == '__main__': # Create a graph given in the above diagram g = Graph(6) g.addEdge(5, 2) g.addEdge(5, 0) g.addEdge(4, 0) g.addEdge(4, 1) g.addEdge(2, 3) g.addEdge(3, 1) print('Following is a Topological Sort of the given graph') g.topologicalSort()> JavaScript // Class to represent a graph class Graph { constructor(V) { this.V = V; // No. of vertices this.adj = new Array(V); // Array containing adjacency lists for (let i = 0; i < V; i++) { this.adj[i] = []; } } // Function to add an edge to the graph addEdge(v, w) { this.adj[v].push(w); // Add w to v’s list. } // Function to perform Topological Sort topologicalSort() { // Create a array to store in-degree of all vertices let inDegree = new Array(this.V).fill(0); // Traverse adjacency lists to fill inDegree of vertices for (let v = 0; v < this.V; v++) { for (let w of this.adj[v]) { inDegree[w]++; } } // Create a queue and enqueue all vertices with in-degree 0 let queue = []; for (let i = 0; i < this.V; i++) { if (inDegree[i] === 0) { queue.push(i); } } // Initialize count of visited vertices let count = 0; // Create an array to store topological order let topOrder = []; // One by one dequeue vertices from queue and enqueue // adjacent vertices if in-degree of adjacent becomes 0 while (queue.length !== 0) { // Extract front of queue and add it to topological order let u = queue.shift(); topOrder.push(u); // Iterate through all its neighboring nodes // of dequeued node u and decrease their in-degree by 1 for (let w of this.adj[u]) { // If in-degree becomes zero, add it to queue if (--inDegree[w] === 0) { queue.push(w); } } count++; } // Check if there was a cycle if (count !== this.V) { console.log('Graph contains cycle'); return; } // Print topological order console.log('Topological Sort of the given graph:'); console.log(topOrder.join(' ')); } } // Driver code // Create a graph given in the above diagram let g = new Graph(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); console.log('Following is a Topological Sort of the given graph:'); g.topologicalSort(); //This code is contributed by Utkarsh> Výkon
Following is a Topological Sort of the given graph 4 5 2 0 3 1>
Časová zložitosť:
Časová zložitosť pre zostavenie grafu je O(V + E), kde V je počet vrcholov a E je počet hrán.
osi referenčný model v sieťovaní
Časová zložitosť pre vykonávanie topologického triedenia pomocou BFS je tiež O(V + E), kde V je počet vrcholov a E je počet hrán. Je to preto, že každý vrchol a každá hrana sa navštívi raz počas prechodu BFS.
Priestorová zložitosť:
Priestorová zložitosť pre uloženie grafu pomocou zoznamu susediacich je O(V + E), kde V je počet vrcholov a E je počet hrán.
Dodatočný priestor sa používa na uloženie stupňov v stupňoch vrcholov, čo si vyžaduje priestor O(V).
Na prechod BFS sa používa front, ktorý môže obsahovať najviac V vrcholov. Priestorová zložitosť pre front je teda O(V).
Celkovo je priestorová zložitosť algoritmu O(V + E) v dôsledku uloženia grafu, in-degree poľa a frontu.
Stručne povedané, časová zložitosť poskytovanej implementácie je O(V + E) a priestorová náročnosť je tiež O(V + E).
Poznámka: Tu môžeme namiesto zásobníka použiť aj pole. Ak sa použije pole, vytlačte prvky v opačnom poradí, aby ste získali topologické triedenie.
Výhody topologického triedenia:
- Pomáha pri plánovaní úloh alebo udalostí na základe závislostí.
- Detekuje cykly v orientovanom grafe.
- Efektívne riešenie problémov s obmedzeniami priority.
Nevýhody topologického triedenia:
- Platí len pre orientované acyklické grafy (DAG), nie je vhodné pre cyklické grafy.
- Nemusí byť jedinečné, môže existovať viacero platných topologických usporiadaní.
- Neefektívne pre veľké grafy s mnohými uzlami a hranami.
Aplikácie topologického triedenia:
- Plánovanie úloh a riadenie projektov.
- Riešenie závislostí v systémoch správy balíkov.
- Určenie poradia kompilácie v systémoch zostavovania softvéru.
- Detekcia uviaznutia v operačných systémoch.
- Rozvrhovanie kurzov na univerzitách.
Súvisiace články:
- Kahnov algoritmus pre topologické triedenie
- Všetky topologické druhy riadeného acyklického grafu