Trigonometria je dôležité odvetvie matematiky, ktoré sa zaoberá vzťahom medzi uhlami a dĺžkami strán pravouhlého trojuholníka. Šesť goniometrických pomerov alebo funkcií je sínus, kosínus, dotyčnica, kosekans a sečna a trigonometrický pomer je pomer medzi stranami pravouhlého trojuholníka. Funkcie sínus, kosínus a tangens sú tri dôležité goniometrické funkcie, pretože ostatné tri, t. j. kosekans, sekans a kotangens, sú recipročné funkcie sínusových, kosínusových a tangensových funkcií.
- sin θ = Opačná strana/hypotenúza
- cos θ = susediaca strana/hypotenúza
- tan θ = Opačná strana/Priľahlá strana
- cosec θ = prepona/opačná strana
- sek θ = prepona/priľahlá strana
- detská postieľka θ = susedná strana/protiľahlá strana
Funkcia dotyčnice je jednou zo 6 goniometrických funkcií používaných v trigonometrických vzorcov .
Obsah
Tangentový vzorec
Tangenta uhla v pravouhlom trojuholníku je pomer dĺžky protiľahlej strany k dĺžke priľahlej strany k danému uhlu. Funkciu dotyčnice píšeme ako tan. Uvažujme pravouhlý trojuholník XYZ a jeden z jeho ostrých uhlov je θ. Opačná strana je strana, ktorá je opačná k uhlu θ a susedná strana je strana, ktorá susedí s uhlom θ.
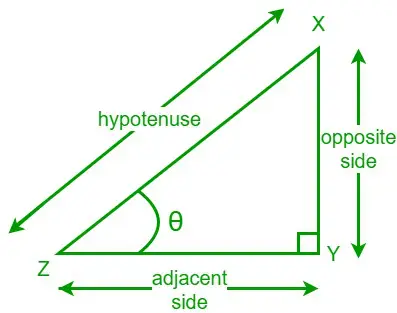
Teraz vzorec dotyčnice pre daný uhol θ je,
tan θ = Opačná strana/Priľahlá strana
Niektoré základné tangentové vzorce
Funkcia dotyčnice v kvadrantoch
Funkcia dotyčnice je kladná v prvom a treťom kvadrante a záporná v druhom a štvrtom kvadrante.
- tan (2π + θ) = tan θ (1svkvadrant)
- tan (π – θ) = – tan θ (2ndkvadrant)
- tan (π + θ) = tan θ (3rdkvadrant)
- tan (2π – θ) = – tan θ (4thkvadrant)
Dotyková funkcia ako negatívna funkcia
Funkcia dotyčnice je negatívna funkcia, pretože dotyčnica záporného uhla je záporná tangens kladného uhla.
tan (-θ) = – tan θ
Funkcia tangens z hľadiska funkcie sínus a kosínus
Funkciu tangens z hľadiska funkcií sínus a kosínus možno zapísať ako,
tan θ = sin θ/cos θ
Vieme to, tan θ = Opačná strana/Priľahlá strana
Teraz rozdeľte čitateľa aj menovateľa s preponou
tan θ = (opačná strana/hypotenza)/(priľahlá strana/hypotenza)
Vieme, že sin θ = opačná strana/hypotenúza
cos θ = susedná strana/hypotenza
Preto tan θ = sin θ/cos θ
Funkcia tangenty z hľadiska funkcie sínusu
Dotykovú funkciu z hľadiska sínusovej funkcie možno zapísať ako,
tan θ = hriech θ/(√1 – hriech 2 i)
My to vieme,
tan θ = sin θ/cos θ
urfi javed
Z pytagorovských identít máme,
bez2θ + cos2θ = 1
cos2θ = 1 – hriech2i
cos θ = √(1 – sin2i)
Preto tan θ = sin θ/(√1 – sin2i)
Funkcia tangenty z hľadiska funkcie kosínus
Dotykovú funkciu z hľadiska kosínusovej funkcie možno zapísať ako,
tan θ = (√1 -cos 2 i)/cos i
My to vieme,
tan θ = sin θ/cos θ
Z pytagorovských identít máme,
bez2θ + cos2θ = 1
bez2θ = 1 – cos2i
sin θ = √(1 – cos2i)
Preto tan θ = (√1 – cos2i)/cos i
Funkcia tangens z hľadiska funkcie kotangens
Funkciu tangens z hľadiska funkcie kotangens možno písať ako,
tan 6 = 1/detská postieľka 9
alebo
tan θ = detská postieľka (90° – θ) (alebo) detská postieľka (π/2 – θ)
Funkcia tangenty v zmysle funkcie kosekantu
Funkciu tangenty z hľadiska funkcie kosekans možno zapísať ako,
tan θ = 1/√ (kosec 2 ja – 1)
Z pytagorovských identít máme,
cosec2θ – detská postieľka2θ = 1
detská postieľka2θ = kosec2ja – 1
detská postieľka θ = √ (kosec2ja – 1)
My to vieme,
tan 6 = 1/detská postieľka 9
Z toho vyplýva, že tan θ = 1/√ (kosec2ja – 1)
Funkcia tangenty v zmysle funkcie sekanty
Funkciu tangens z hľadiska funkcie sekans možno zapísať ako,
tan θ = √sek 2 ja – 1
Z pytagorovských identít máme,
sek2θ – teda2θ = 1
tan θ = sek2ja – 1
Preto tan θ = √ (sek2ja – 1)
Funkcia dotyčnice z hľadiska dvojitého uhla
Funkcia dotyčnice pre dvojitý uhol je,
tan 2θ = (2 tan θ)/(1 – tan 2 i)
Funkcia dotyčnice z hľadiska trojitého uhla
Funkcia dotyčnice pre trojitý uhol je,
tan 3θ = (3 tan θ – tan 3 θ) / (1 – 3 tan 2 i)
Funkcia dotyčnice v zmysle polovičného uhla
Funkcia dotyčnice pre polovičný uhol je,
tan (θ/2) = ± √[ (1 – cos θ) / (1 + cos θ) ]
tan (θ/2) = (1 – cos θ) / ( sin θ)
Funkcia dotyčnice z hľadiska sčítania a odčítania dvoch uhlov
Vzorce súčtu a rozdielu pre funkciu dotyčnice sú,
tan (A + B) = (tan A + tan B)/(1 – tan A tan B)
opálenie (A – B) = (opálenie A – opálenie B)/(1 + opálenie A opálenie B)
Tabuľka trigonometrických pomerov
| Uhol (v stupňoch) | Uhol (v radiánoch) | hriech i | cos θ | tan θ = sin θ/cos θ | cosec θ | sek θ | detská postieľka i |
|---|---|---|---|---|---|---|---|
| 0° | 0 | 0 | 1 | 0/1 = 0 | Nedefinované | 1 | Nedefinované |
| 30° | p/6 | 1/2 | √3/2 | (1/2)/(√3/2) = 1/√3 | 2 | 23 | √3 |
| 45° | p/4 | 1/√2 | 1/√2 | (1/√2)/(1/√2) = 1 | √2 | √2 | 1 |
| 60° | p/3 | √3/2 | 1/2 | (√3/2)/(1/2) = √3 reťazec nájsť c++ | 23 | 2 | 1/√3 |
| 90° | p/2 | 1 | 0 | 1/0 = nedefinované | 1 | Nedefinované | 0 |
| 120° | 2p/3 | √3/2 | -1/2 | (√3/2)/(-1/2) = -√3 | 23 | -2 | -1/√3 |
| 150° | 5p/6 | 1/2 | -(√3/2) | (1/2)/(-√3/2) = -1/√3 | 2 | -(23) | -√3 |
| 180° | Pi | 0 | -1 | 0/(-1) = 0 | Nedefinované | -1 | Nedefinované |
Vyriešený príklad na tangensových vzorcoch
Príklad 1: Nájdite hodnotu tan θ, ak sin θ = 2/5 a θ je uhol prvého kvadrantu.
Riešenie:
Vzhľadom na to,
- sin θ = 2/5
Z pytagorovských identít, ktoré máme,
bez2θ + cos2θ = 1
cos2θ = 1 – hriech2θ = 1 – (2/5)2
cos2θ = 1 – (4/5) = 21/25
cos θ = ±√21/5
Pretože θ je uhol prvého kvadrantu, cos θ je kladné.
prevod reťazca na int javacos θ = √21/5
My to vieme,
tan θ = sin θ/cos θ
= (2/5)/(√21/5) = 2/√21
tan θ = 2√21/21
Takže hodnota tan θ, keď sin θ = 2/5 a θ je v prvom kvadrante, je (2√21) /(21)
Príklad 2: Nájdite hodnotu tan x, ak sek x = 13/12 a x je štvrtý kvadrantový uhol.
Riešenie:
Dané, sek x = 13/12
Z pytagorovských identít máme,
sek2x – teda2x = 1
tak2x = sek2x – 1= (13/12)2- 1
tak2x = (169/144) – 1 = 25/144
tan x = ± 5/12
Pretože x je štvrtý kvadrantový uhol, tan x je záporné.
tan x = – 5/12
teda tan x = – 5/12
Príklad 3: Ak tan X = 2/3 a tan Y = 1/2, aká je potom hodnota tan (X + Y)?
Riešenie:
Vzhľadom na to,
tan X = 2/3 a tan Y = 1/2
My to vieme,
tan (X + Y) = (tan X + tan Y)/(1 – tan X tan Y)
tan (X + Y) = [(2/3) + (1/2)]/[1 – (2/3)×(1/2)]
= (7/6)/(2/3) = 7/4
teda tan(X + Y) = 7/4
Príklad 4: Vypočítajte funkciu dotyčnice, ak susedné a protiľahlé strany pravouhlého trojuholníka sú 4 cm a 7 cm.
Riešenie:
Vzhľadom na to,
Susedná strana = 4 cm
Opačná strana = 7 cm
My to vieme,
tan θ = Opačná strana/Priľahlá strana
tan 6 = 7/4 = 1,75
teda tan 6 = 1,75
Príklad 5: Muž sa pozerá na hodinovú vežu pod uhlom 60° k vrcholu veže, ktorej výška je 100 m. Aká je vzdialenosť medzi človekom a pätou veže?
Riešenie:
Vzhľadom na to,
Výška veže = 100 m a θ = 60°
Nech vzdialenosť medzi človekom a nohou veže = d
Máme,
tan θ = Opačná strana/Priľahlá strana
tan 60° = 100/d
√3 = 100/d [Odkedy, tak 60° = √3]
d = 100/√3
Preto je vzdialenosť medzi človekom a pätou veže 100/√3
Príklad 6: Nájdite hodnotu tan θ, ak sin θ = 7/25 a sec θ = 25/24.
Riešenie:
Vzhľadom na to,
sin θ = 7/25
sek. 0 = 25/24
My to vieme,
sek. 0 = 1/cos 9
25/24 = 1/cos θ cos θ = 24/25
Máme,
tan θ = sin θ/cos θ
= (7/25)/(24/25)
= 7/24
teda tan 6 = 7/24
Príklad 7: Nájdite hodnotu tan θ, ak cosec θ = 5/3 a θ je uhol prvého kvadrantu.
Riešenie:
Dané, cosec θ = 5/3
Z pytagorovských identít máme,
string.format javacosec2θ – detská postieľka2θ = 1
detská postieľka2θ = kosec2ja – 1
detská postieľka θ = (5/3)2– 1 = (25/9) – 1 = 16/9
detská postieľka θ = ±√16/9 = ± 4/3
Keďže θ je uhol prvého kvadrantu, kotangens aj tangens funkcie sú kladné.
detská postieľka θ = 4/3
My to vieme,
detská postieľka 9 = 1/tan 9
4/3 = 1/tan8
tan 6 = 3/4
teda tan 6 = 3/4
Príklad 8: Nájdite tan 3θ, ak sin θ = 3/7 a θ je uhol prvého kvadrantu.
Riešenie :
Dané, hriech θ = 12/13
Z pytagorovských identít, ktoré máme,
bez2θ + cos2θ = 1
cos2θ = 1 – hriech2θ = 1 – (12/13)2
cos2 θ = 1 – (144/169) = 25/169
cos θ = ±√25/169 = ±5/13
Pretože θ je uhol prvého kvadrantu, cos θ je kladné.
cos 0 = 5/13
My to vieme,
tan θ = sin θ/cos θ
= (12/25)/(5/13) = 12/5
Z toho vyplýva, že tan θ = 12/5
Teraz vieme, že
tan 3θ = (3 tan θ – tan3θ) / (1 – 3 tan2θ)
tan 3θ = 3 × (12/5)

