Štandardný tvar paraboly je y = ax²+ bx + c kde a, b a c sú reálne čísla a a sa nerovná nule. Parabola je definovaná ako množina všetkých bodov v rovine, ktoré sú rovnako vzdialené od pevnej čiary a pevného bodu v rovine.

V tomto článku pochopíme, čo je Parabola, štandardná rovnica Paraboly, súvisiace príklady a ďalšie podrobnosti.

Obsah

• Čo je to parabola?
• Rovnica paraboly
• Všeobecné rovnice paraboly
• Štandardné rovnice paraboly
• Časti paraboly
• Príklady rovnice paraboly

Čo je to parabola?

Parabola je kužeľosečka definovaná ako množina všetkých bodov rovnako vzdialených od bodu nazývaného ohnisko a priamky nazývanej priamka. Štandardné rovnice pre parabolu závisia od jej orientácie (smeru otvárania) a polohy.

Rovnica paraboly

Rovnica paraboly môže byť napísaná v štandardnej forme alebo všeobecnej forme a obe sú pridané nižšie:

Všeobecné rovnice paraboly

Všeobecná rovnica paraboly je,

y = 4a (x – h) ² + k

(alebo)

x = 4a(y – k) ² + h

Kde (h, k) je vrchol paraboly.

Štandardné rovnice paraboly

Štandardná rovnica paraboly je,

y = sekera ² + bx + c

(alebo)

x = je ² + o + c

kde a nikdy nemôže byť nula.

Časti paraboly

Niektoré dôležité pojmy a časti paraboly sú:

• Zameranie: Ohnisko je pevný bod paraboly.

• Directrix: Smernica paraboly je priamka kolmá na os paraboly.

• Ohniskový akord: Tetiva, ktorá prechádza ohniskom paraboly a pretína parabolu v dvoch odlišných bodoch, sa nazýva ohnisková struna.

• Ohnisková vzdialenosť: Ohnisková vzdialenosť je vzdialenosť bodu (x₁, a₁) na parabole z ohniska.

• Pravá strana: Latus rectum je ohnisková struna, ktorá prechádza ohniskom paraboly a je kolmá na os paraboly. Dĺžka latus rectum je LL‘ = 4a.

• Excentricita: Pomer vzdialenosti bodu od ohniska k jeho vzdialenosti od smerovej čiary sa nazýva excentricita (e). Pre parabolu sa excentricita rovná 1, t.j. e = 1.

Parabola má štyri štandardné rovnice založené na orientácii paraboly a jej osi. Každá parabola má inú priečnu os a konjugovanú os.

Parabolická rovnica	Parabola	Vzorce parametrov paraboly
a 2 = 4ax	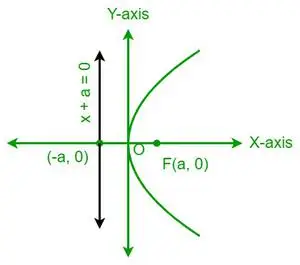Horizontálna parabola	Vertex = (0,0) Zameranie = (a, 0) Parabola sa otvára na pravú stranu. Osová rovnica je y = 0 Rovnica smerovej čiary je x + a = 0 Dĺžka latus rectum = 4a
a 2 = -4ax	Horizontálna parabola	Vertex = (0,0) Zameranie = (-a, 0) Parabola sa otvára na ľavú stranu. Osová rovnica je y = 0 Smerová rovnica je x – a = 0 Dĺžka latus rectum = 4a
X 2 = 4 ay	Vertikálna parabola	Vertex = (0,0) Zameranie = (0, a) Parabola sa otvára smerom nahor. Osová rovnica je x = 0 Rovnica smerovej čiary je y + a = 0 Dĺžka latus rectum = 4a
X 2 = -4 ay	Vertikálna parabola	Vertex = (0,0) Zameranie = (0, -a) Parabola sa otvára smerom nadol. Osová rovnica je x = 0 Smernicová rovnica je y – a = 0 Dĺžka latus rectum = 4a

Nasledujú pozorovania zo štandardného tvaru rovníc paraboly:

• Parabola je symetrická so svojou osou. Napríklad y²= 4ax je symetrický vzhľadom na os x, zatiaľ čo x²= 4ay je symetrický vzhľadom na os y.

• Ak je parabola symetrická podľa osi x, potom sa parabola otvára smerom doprava, ak je koeficient x kladný, a smerom doľava, ak je koeficient x záporný.

• Ak je parabola symetrická podľa osi y, potom sa parabola otvára smerom nahor, ak je koeficient y kladný, a smerom nadol, ak je koeficient y záporný.

Nasledujú štandardné rovnice paraboly, keď je os symetrie rovnobežná s osou x alebo osou y a vrchol nie je v počiatku.

Parabolová rovnica	Parabola	Vzorce parametrov paraboly
(a – k)2= 4a(x – h)	Horizontálna parabola	Vrchol = (h, k) Zameranie = (h + a, k) Parabola sa otvára na pravú stranu. Osová rovnica je y = k Rovnica smerovej čiary je x = h – a Dĺžka latus rectum = 4a
(a – k)2= -4a(x – h)	Horizontálna parabola	Vrchol = (h, k) Ohnisko = (h – a, k) Parabola sa otvára na ľavú stranu. Osová rovnica je y = k Rovnica smerovej čiary je x = h + a Dĺžka latus rectum = 4a
(x – h)2= 4a(y – k)	Vertikálna parabola	Vrchol = (h, k) Zaostrenie = (h, k + a) Parabola sa otvára smerom nahor. Osová rovnica je x = h Smernicová rovnica je y = k – a Dĺžka latus rectum = 4a
(x – h)2= -4a(y – k)	Vertikálna parabola	Vrchol = (h, k) Ohnisko = (h, k – a) Parabola sa otvára smerom nadol. Osová rovnica je x = h Rovnica smerovej čiary je y = k + a Dĺžka latus rectum = 4a

Rovnica odvodenia paraboly

Nech P je bod na parabole, ktorého súradnice sú (x, y). Z definície paraboly je vzdialenosť bodu P k ohnisku (F) rovná vzdialenosti toho istého bodu P k priamke paraboly. Teraz uvažujme bod X na priamke, ktorého súradnice sú (-a, y).

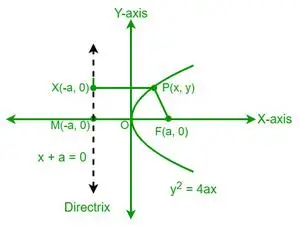
Z definície excentricity paraboly máme

e = PF/PX = 1

⇒ PF = PX

Súradnice ohniska sú (a, 0). Teraz pomocou vzorca súradnicovej vzdialenosti môžeme nájsť vzdialenosť bodu P (x, y) k ohnisku F (a, 0).

PF = √[(x – a)²+ (a – 0)²]

⇒ PF = √[(x – a)²+ a²] ------ (1)

Rovnica riadiacej čiary je x + a = 0. Na zistenie vzdialenosti PX použijeme vzorec kolmej vzdialenosti.

PX = (x + a)/√[1²+0²]

⇒ PX = x +a —————— (2)

Už vieme, že PF = PX. Takže prirovnajte rovnice (1) a (2).

√[(x – a)²+ a²] = (x + a)

Vyrovnaním na oboch stranách dostaneme,

⇒ [(x – a)²+ a²] = (x + a)²

⇒ x²+ a²– 2ax + y²= x²+ a²+ 2ax

⇒ a²– 2ax = 2ax

⇒ a²= 2ax + 2ax ⇒ a ² = 4ax

Takto sme odvodili rovnicu paraboly. Podobne môžeme odvodiť štandardné rovnice ďalších troch parabol.

• a²= -4ax
• X²= 4 ay
• X²= -4 ay

a ² = 4ax, a ² = -4ax, x ² = 4ay a x ² = -4 ay sú štandardné rovnice paraboly.

Články súvisiace s Parabola:

• Kruhová rovnica
• Elipsová rovnica
• Hyperbola
• Aplikácie Paraboly v reálnom živote

Príklady rovnice paraboly

Príklad 1: Nájdite dĺžku latového rekta, ohniska a vrcholu, ak rovnica paraboly je y ² = 12x.

Riešenie:

Vzhľadom na to,

Rovnica paraboly je y²= 12x

Porovnaním danej rovnice so štandardným tvarom y²= 4ax

4a = 12

⇒ a = 12/4 = 3

My to vieme,

Pravá strana paraboly = 4a = 4 (3) = 12

Teraz ohnisko paraboly = (a, 0) = (3, 0)

Vrchol danej paraboly = (0, 0)

Príklad 2: Nájdite rovnicu paraboly, ktorá je symetrická podľa osi X a prechádza bodom (-4, 5).

Riešenie:

Vzhľadom na to,

Parabola je symetrická okolo osi X a má svoj vrchol v počiatku.

Rovnica teda môže mať tvar y²= 4ax alebo y²= -4ax, kde znamienko závisí od toho, či sa parabola otvára smerom doľava alebo doprava.

Parabola sa musí otvárať vľavo, pretože prechádza cez (-4, 5), ktorý leží v druhom kvadrante.

Takže rovnica bude: y²= -4ax

Nahradením (-4, 5) vo vyššie uvedenej rovnici

⇒ (5)²= -4a(-4)

⇒ 25 = 16a

⇒ a = 25/16

Preto rovnica paraboly je: y²= -4(25/16)x (alebo) 4r²= -25x.

Príklad 3: Nájdite súradnice ohniska, osi, rovnicu priamej čiary a latus rectum paraboly x ² = 16r.

Riešenie:

Vzhľadom na to,

Rovnica paraboly je: x²= 16r

Porovnaním danej rovnice so štandardným tvarom x²= 4 ay,

4a = 16 ⇒ a = 4

Koeficient y je kladný, takže parabola sa otvára smerom nahor.

Tiež os symetrie je pozdĺž kladnej osi Y.

teda

Ohnisko paraboly je (a, 0) = (4, 0).

Rovnica smerovej čiary je y = -a, t.j. y = -4 alebo y + 4 = 0.

Dĺžka latus rectum = 4a = 4(4) = 16.

Príklad 4: Nájdite dĺžku latového rekta, ohniska a vrcholu, ak rovnica paraboly je 2(x-2) ² + 16 = y.

Riešenie:

Vzhľadom na to,

Rovnica paraboly je 2 (x-2)²+ 16 = a

Porovnaním danej rovnice so všeobecnou rovnicou paraboly y = a(x – h)²+ k, dostaneme

a = 2

(h, k) = (2, 16)

My to vieme,

Dĺžka latus rectum paraboly = 4a

= 4(2) = 8

Teraz zaostrite = (a, 0) = (2, 0)

Teraz, Vertex = (2, 16)

Príklad 5: Rovnica paraboly je x ² – 12x + 4y – 24 = 0, potom nájdite jeho vrchol, ohnisko a smerovú čiaru.

Riešenie:

Vzhľadom na to,

Rovnica paraboly je x²– 12x + 4 roky – 24 = 0

⇒ x²– 12x + 36 – 36 + 4 roky – 24 = 0

⇒ (x – 6)²+ 4 roky – 60 = 0

⇒ (x – 6)²= -4 (y + 15)

Získaná rovnica je v tvare (x – h)²= -4a(y – k)

-4a = -4 ⇒ a = 1

Takže vrchol = (h, k) = (6, – 15)

Zaostrenie = (h, k – a) = (6, -15-1) = (6, -16)

Rovnica smerovej čiary je y = k + a

⇒ y = -15 + 1 ⇒ y = -14

⇒ y + 14 = 0

Časté otázky o rovnici paraboly

Ako zistíte štandardnú rovnicu paraboly?

Štandardná forma paraboly je y²= 4ax alebo x²= 4 ay.

Aká je normálna rovnica paraboly?

Rovnica normály k parabole y²= 4ax so sklonom m je dané ako: y = mx – 2:00 – ráno ³

Ako zistíte vrchol paraboly?

Pre danú parabolu: y = ax²+ bx + c jeho vrchol možno nájsť pomocou vzorca x = − b/2a. Vložte túto hodnotu x späť do rovnice, aby ste našli zodpovedajúcu súradnicu y.

ako sťahovať hudbu