Kvadrant je definovaná ako oblasť v priestore, ktorá je rozdelená na štyri rovnaké časti dvoma osami, a to osou X a osou Y v karteziánskej rovine. Tieto dve osi sa navzájom pretínajú v 90 stupňoch a štyri takto vytvorené oblasti sa nazývajú štyri kvadranty, konkrétne I kvadrant, II kvadrant, III kvadrant a IV kvadrant.
reťazcový formát v jazyku Java
V tomto článku preskúmame základné kvadrantové koncepty vrátane toho, čo je kvadrant, jeho plocha, kvadrantový graf, karteziánska rovina, znamienkové konvencie v kvadrante, úsečka a súradnice, ako aj vykresľovanie bodov na kvadrante.
Obsah
- Čo sú kvadranty grafu?
- Podpísať dohovor v kvadrantoch
- Vykresľovanie bodov na kvadrantoch
- Trigonometrické hodnoty v rôznych kvadrantoch
Čo sú kvadranty grafu?
Kvadrant je určená oblasť na a Kartézska rovina , vytvorený priesečníkom osí X a Y. V tejto rovine sú vytvorené štyri kvadranty, z ktorých každý má svoje jedinečné vlastnosti. Prvý kvadrant v pravom hornom rohu má kladné súradnice x a y. Druhý kvadrant vľavo hore má záporné súradnice x a kladné súradnice y atď. Pochopenie týchto kvadrantov je nevyhnutné na lokalizáciu a interpretáciu bodov na grafe, čo poskytuje systematický spôsob navigácie a analýzy karteziánskych súradníc.
4 kvadranty na súradnicovej rovine
Kartézska rovina, tvorená osami X a Y, je rozdelená do štyroch kvadrantov, z ktorých každý má odlišné charakteristiky:
- Prvý kvadrant: Súradnice x aj y sa nachádzajú v pravom hornom rohu a sú kladné. Tento kvadrant predstavuje body v pravej hornej časti roviny.
- Druhý kvadrant: V ľavom hornom rohu je súradnica x záporná a súradnica y kladná. Tento kvadrant pokrýva body v ľavej hornej časti roviny.
- Tretí kvadrant: Súradnice x aj y sú v ľavom dolnom rohu záporné. Do tohto kvadrantu spadajú body v ľavej dolnej časti roviny.
- Štvrtý kvadrant: V pravom dolnom rohu je súradnica x kladná a súradnica y záporná. Tento kvadrant obsahuje body v pravej dolnej časti roviny.
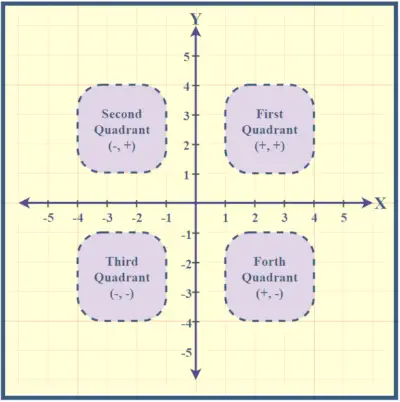
Kvadranty sú očíslované proti smeru hodinových ručičiek, začínajúc vpravo hore. Bod, kde sa pretínajú osi X a Y, sa nazýva počiatok so súradnicami (0,0), ktoré označujú nulové hodnoty pre x aj y. Pochopenie týchto kvadrantov pomáha lokalizovať body v karteziánskej rovine.
Čo je pôvod?
Počiatočný bod grafu, známy ako počiatok a zobrazený ako (0, 0), je miesto, kde sa pretínajú horizontálna os x a vertikálna os y. To znamená, že na začiatku sú hodnoty x aj y nulové. Slúži ako referenčný bod na lokalizáciu ďalších bodov v grafe. Na obrázku pridanom nad bod O ukazuje pôvod.
Úsečka a súradnica v kvadrantoch
V štyroch kvadrantoch sú čísla reprezentované ako páry (a, b), kde „a“ predstavuje súradnicu x a „b“ predstavuje súradnicu y. Ak chcete zistiť, kde je bod bez vykreslenia, venujte pozornosť znamienkam súradnice x (úsečka) a súradnice y (osová súradnica). Napríklad, ak máte bod ako Q (3, -5), znamienka (+ve, -ve) označujú, že je v kvadrante IV.
Vodorovná os ukazuje horizontálnu vzdialenosť od osi Y. Kladná abscisa znamená doprava a v našom príklade abscisa = 3 znamená ísť doprava od začiatku pozdĺž osi x o 3 jednotky.
Ordináta označuje vertikálnu vzdialenosť od začiatku. Záporná ordináta znamená ísť dole od začiatku pozdĺž osi y. V tomto príklade ordináta = -5 znamená zníženie o 5 jednotiek.
Podpísať dohovor v kvadrantoch
Znakové konvencie v kvadrantoch možno ľahko pochopiť pomocou obrázka pridaného nižšie,

V rovine XY, keď sa pohybujeme zľava doprava pozdĺž osi x, súradnica x sa zvyšuje. Podobne, pozdĺž osi y, pohyb zdola nahor vedie k zvýšeniu súradnice y. Rovina XY je rozdelená do štyroch kvadrantov, z ktorých každý má špecifické znamienka pre súradnice x a y:
| Kvadrant | x-ová súradnica | y-ová súradnica |
|---|---|---|
| 1. kvadrant | pozitívne (+) | pozitívne (+) |
| 2. kvadrant | záporné (-) | pozitívne (+) |
| 3. kvadrant | záporné (-) | záporné (-) |
| 4. kvadrant | pozitívne (+) | záporné (-) |
Preto body v 1. kvadrante majú kladné hodnoty pre x aj y, body v 2. kvadrante majú záporné x a kladné y, 3. kvadrant má záporné hodnoty x aj y a 4. kvadrant má kladné x a záporné y.
Vykresľovanie bodov na kvadrantoch
V karteziánskej rovine sú body označené osou x a osou y. Tieto body sú označené ako (a, b), kde „a“ je x-ová súradnica (abscisa) a „b“ je súradnica y (ordináta). Na umiestnenie bodu v kvadrante berieme do úvahy znamienka týchto súradníc. Hodnoty x a y predstavujú vzdialenosť bodu od osi x a osi y.
Napríklad nakreslite bod (2, -5) na karteziánsku rovinu. Analýza znamienka súradníc odhalí, že bod je v 4. kvadrante. Bude vzdialený 2 jednotky od osi x (vpravo) a 5 jednotiek od osi y (dole), pričom ako referenčný bod sa použije počiatok.
Trigonometrické hodnoty v rôznych kvadrantoch
Hodnoty rôznych goniometrické funkcie v rôznych kvadrantoch sa môžete naučiť preštudovaním tabuľky pridanej nižšie ako,
| Kvadrant | Bez | Cos | Takže | Cosecant | Secant | Kotangens |
|---|---|---|---|---|---|---|
| 1. kvadrant | + | + | + | + | + | + |
| 2. kvadrant | + | – | + | + | – | – |
| 3. kvadrant java boolean | – | – | – | – | – | + |
| 4. kvadrant | – | – java stack | – | – | + | – |
V 1. kvadrante sú všetky trigonometrické pomery kladné. V 2. kvadrante sú sínus a kosekant kladné (+), zatiaľ čo kosínus a sekant sú záporné (-). V 3. kvadrante sú tangens a kotangens kladné (+), zatiaľ čo kosínus a sekant sú záporné (-). V 4. kvadrante sú sínus a kosekant záporné (-), zatiaľ čo kosínus a sekans sú kladné (+).
Čítaj viac,
- Geometria súradníc
- Paralelné čiary
- Vzorec vzdialenosti
Vyriešené príklady v kvadrante
Príklad 1: Nakreslite bod A (3, -4) a identifikujte jeho kvadrant.
Riešenie:
Bod A sa nachádza na súradniciach (3, -4). Keďže súradnica x je kladná (3) a súradnica y záporná (-4), bod A leží v IV. kvadrante.
Príklad 2: Nakreslite bod P (-5, 2) a určte jeho kvadrant
Riešenie:
Súradnice bodu P sú (-5, 2). Na určenie kvadrantu skúmame znamienka súradníc x a y.
X-ová súradnica je -5, čo označuje polohu naľavo od počiatku.
Súradnica Y je 2, čo označuje polohu nad počiatkom.
Preto, keďže súradnica x je záporná a súradnica y kladná, bod P sa nachádza v kvadrante II.
Bod P (-5, 2) sa nachádza v II. kvadrante karteziánskej roviny.
Cvičné problémy v kvadrantoch
Problém 1: Nakreslite bod (1, -1) a identifikujte jeho kvadrant.
Problém 2: Nájdite tri body na osi x a určte ich kvadranty.
Problém 3: Ak bod leží na osi y so súradnicami (0, -3), v ktorom kvadrante sa nachádza?
Problém 4: Nájdite body Q (2, 2), R (-2, -2) a S (0, 0) a skontrolujte kolinearitu.
Problém 5: Nakreslite bod (-4, -3) a vysvetlite, v ktorom kvadrante sa nachádza.
Časté otázky o kvadrantoch
1. Čo je to kvadrant v matematike?
V matematike je kvadrant jedným zo štyroch úsekov vytvorených priesečníkom dvoch na seba kolmých čiar alebo osí. Tieto osi sú zvyčajne označené ako os x a os y v karteziánskom súradnicovom systéme.
2. Ako sa nazýva priesečník dvoch osí?
Priesečník dvoch osí v karteziánskom súradnicovom systéme sa nazýva počiatok. Je reprezentovaný bodom, kde sa stretáva os x a os y, zvyčajne označovaný ako (0,0).
3. Čo sú to 4 kvadranty?
Štyri kvadranty sú sekcie vytvorené rozdelením karteziánskej súradnicovej roviny na štyri rovnaké časti. Sú označené ako prvý kvadrant (Q1), druhý kvadrant (Q2), tretí kvadrant (Q3) a štvrtý kvadrant (Q4).
4. Ktorý kvadrant je pozitívny?
Kladný kvadrant v karteziánskom súradnicovom systéme je prvý kvadrant (Q1). V tomto kvadrante sú súradnice x aj y kladné.
5. Aké je použitie kvadrantov v grafoch?
Kvadranty v grafoch poskytujú systematický spôsob organizácie a lokalizácie bodov na základe ich súradníc. Pomáhajú pri vizualizácii vzťahov medzi premennými a analýze vzorov v súboroch údajov, čím uľahčujú interpretáciu grafických zobrazení.
6. Ktorý kvadrant má obe hodnoty súradníc kladné?
Prvý kvadrant (Q1) je kvadrant, v ktorom sú súradnice x aj y bodov kladné. Je to jediný kvadrant s oboma kladnými hodnotami.
7. Aké sú 4 kvadranty kruhu?
Koncept kvadrantov nie je priamo aplikovateľný na kruhy. Namiesto toho sú kruhy rozdelené na uhly merané v stupňoch. Ak však hovoríme o kruhových sektoroch, môžeme použiť výrazy ako prvý sektor, druhý sektor, tretí sektor a štvrtý sektor, ktoré zodpovedajú rôznym uhlovým regiónom.
