Logistická regresia v R Programming je klasifikačný algoritmus používaný na nájdenie pravdepodobnosti úspechu a zlyhania udalosti. Logistická regresia sa používa, keď je závislá premenná binárna (0/1, pravda/nepravda, áno/nie). Funkcia logit sa používa ako spojovacia funkcia v binomickom rozdelení.
Pravdepodobnosť binárnej výslednej premennej možno predpovedať pomocou techniky štatistického modelovania známej ako logistická regresia. Je široko používaný v mnohých rôznych odvetviach vrátane marketingu, financií, spoločenských vied a lekárskeho výskumu.
Logistická funkcia, bežne označovaná ako sigmoidná funkcia, je základnou myšlienkou logistickej regresie. Táto sigmoidná funkcia sa používa v logistickej regresii na opis korelácie medzi prediktorovými premennými a pravdepodobnosťou binárneho výsledku.

Logistická regresia v R programovaní
Logistická regresia je známa aj ako Binomická logistická regresia . Je založená na sigmoidnej funkcii, kde výstupom je pravdepodobnosť a vstup môže byť od -nekonečna do +nekonečna.
teória
Logistická regresia je známa aj ako zovšeobecnený lineárny model. Keďže sa používa ako klasifikačná technika na predpovedanie kvalitatívnej odozvy, hodnota y sa pohybuje od 0 do 1 a môže byť vyjadrená nasledujúcou rovnicou:

Logistická regresia v programovaní R
p je pravdepodobnosť záujmovej charakteristiky. Pomer šancí je definovaný ako pravdepodobnosť úspechu v porovnaní s pravdepodobnosťou zlyhania. Je to kľúčová reprezentácia koeficientov logistickej regresie a môže nadobúdať hodnoty medzi 0 a nekonečnom. Pomer šancí 1 je, keď sa pravdepodobnosť úspechu rovná pravdepodobnosti zlyhania. Pomer šancí 2 je, keď je pravdepodobnosť úspechu dvojnásobná ako pravdepodobnosť zlyhania. Pomer šancí 0,5 je, keď je pravdepodobnosť neúspechu dvojnásobkom pravdepodobnosti úspechu.
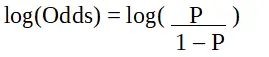
Logistická regresia v programovaní R
Keďže pracujeme s binomickým rozdelením (závislá premenná), musíme zvoliť funkciu prepojenia, ktorá je pre toto rozloženie najvhodnejšia.
sada pružinových nástrojov
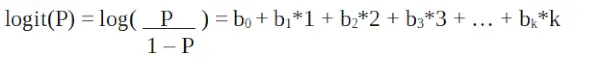
Logistická regresia v R programovaní
Je to a funkcia logit . Vo vyššie uvedenej rovnici je zátvorka zvolená tak, aby maximalizovala pravdepodobnosť pozorovania hodnôt vzorky a nie minimalizovala súčet štvorcových chýb (ako obyčajná regresia). Logit je tiež známy ako denník šancí. Logitová funkcia musí byť lineárne spojená s nezávislými premennými. Toto je z rovnice A, kde ľavá strana je lineárna kombinácia x. Je to podobné predpokladu OLS, že y je lineárne spojené s x. Premenné b0, b1, b2 ... atď sú neznáme a musia sa odhadnúť na základe dostupných tréningových údajov. V modeli logistickej regresie sa vynásobením b1 jednou jednotkou zmení logit b0. Zmeny P v dôsledku zmeny o jednu jednotku budú závisieť od vynásobenej hodnoty. Ak je b1 kladné, P sa zvýši a ak je b1 záporné, P sa zníži.
Súbor údajov
mtcars (motor trend car road test) zahŕňa spotrebu paliva, výkon a 10 aspektov automobilového dizajnu pre 32 automobilov. Dodáva sa s predinštalovaným dplyr balík v R.
R
# Installing the package> install.packages>(>'dplyr'>)> # Loading package> library>(dplyr)> # Summary of dataset in package> summary>(mtcars)> |
>
vypnutie režimu vývojára
>
Vykonávanie logistickej regresie na množine údajov
Logistická regresia je implementovaná v R pomocou glm() trénovaním modelu pomocou funkcií alebo premenných v množine údajov.
R
# Installing the package> # For Logistic regression> install.packages>(>'caTools'>)> # For ROC curve to evaluate model> install.packages>(>'ROCR'>)> > # Loading package> library>(caTools)> library>(ROCR)> |
>
>
Rozdelenie údajov
R
# Splitting dataset> split <->sample.split>(mtcars, SplitRatio = 0.8)> split> train_reg <->subset>(mtcars, split ==>'TRUE'>)> test_reg <->subset>(mtcars, split ==>'FALSE'>)> # Training model> logistic_model <->glm>(vs ~ wt + disp,> >data = train_reg,> >family =>'binomial'>)> logistic_model> # Summary> summary>(logistic_model)> |
>
>
Výkon:
pre každý strojopis
Call: glm(formula = vs ~ wt + disp, family = 'binomial', data = train_reg) Deviance Residuals: Min 1Q Median 3Q Max -1.6552 -0.4051 0.4446 0.6180 1.9191 Coefficients: Estimate Std. Error z value Pr(>|z|) (Zachytenie) 1,58781 2,60087 0,610 0,5415 hmotn. 1,36958 1,60524 0,853 0,3936 rozt. --- Signif. kódy: 0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 ' ' 1 (Parameter rozptylu pre binomickú rodinu sa považuje za 1) Nulová odchýlka: 34,617 na 24 stupňoch voľnosti Zvyšková odchýlka: 20,21 22 stupňov voľnosti AIC: 26,212 Počet iterácií Fisherovho skóre: 6>
- Volanie: Zobrazí sa volanie funkcie použité na prispôsobenie modelu logistickej regresie spolu s informáciami o rodine, vzorci a údajoch. Zvyšky odchýlky: Toto sú zvyšky odchýlky, ktoré merajú stupeň zhody modelu. Predstavujú nezrovnalosti medzi skutočnými odpoveďami a pravdepodobnosťou predpovedanou modelom logistickej regresie. Koeficienty: Tieto koeficienty v logistickej regresii predstavujú logaritmus alebo logit premennej odozvy. Smerodajné chyby súvisiace s odhadovanými koeficientmi sú uvedené v Std. Chybový stĺpec. Kódy významnosti: Úroveň významnosti každej prediktorovej premennej označujú kódy významnosti. Parameter disperzie: V logistickej regresii slúži parameter disperzie ako parameter škálovania pre binomickú distribúciu. V tomto prípade je nastavená na 1, čo znamená, že predpokladaný rozptyl je 1. Nulová odchýlka: Nulová odchýlka vypočíta odchýlku modelu, keď sa berie do úvahy len priesečník. Symbolizuje odchýlku, ktorá by bola výsledkom modelu bez prediktorov. Zvyšková odchýlka: Zvyšková odchýlka vypočítava odchýlku modelu po prispôsobení prediktorov. Znamená zvyškovú odchýlku po zohľadnení prediktorov. AIC: Akaike Information Criterion (AIC), ktoré zodpovedá počtu prediktorov, je meradlom vhodnosti modelu. Penalizuje zložitejšie modely, aby sa predišlo nadmernému vybaveniu. Lepšie padnúce modely sú označené nižšími hodnotami AIC. Počet iterácií Fisherovho skórovania: Počet iterácií, ktoré potrebuje postup Fisherovho skórovania na odhadnutie parametrov modelu, je indikovaný počtom iterácií.
Predpovedajte testovacie údaje na základe modelu
R
predict_reg <->predict>(logistic_model,> >test_reg, type =>'response'>)> predict_reg> |
>
>
Výkon:
Hornet Sportabout Merc 280C Merc 450SE Chrysler Imperial 0.01226166 0.78972164 0.26380531 0.01544309 AMC Javelin Camaro Z28 Ford Pantera L 0.06104267 0.02807992 0.01107943>
R
# Changing probabilities> predict_reg <->ifelse>(predict_reg>0,5, 1, 0)> # Evaluating model accuracy> # using confusion matrix> table>(test_reg$vs, predict_reg)> missing_classerr <->mean>(predict_reg != test_reg$vs)> print>(>paste>(>'Accuracy ='>, 1 - missing_classerr))> # ROC-AUC Curve> ROCPred <->prediction>(predict_reg, test_reg$vs)> ROCPer <->performance>(ROCPred, measure =>'tpr'>,> >x.measure =>'fpr'>)> auc <->performance>(ROCPred, measure =>'auc'>)> auc <- [email protected][[1]]> auc> # Plotting curve> plot>(ROCPer)> plot>(ROCPer, colorize =>TRUE>,> >print.cutoffs.at =>seq>(0.1, by = 0.1),> >main =>'ROC CURVE'>)> abline>(a = 0, b = 1)> auc <->round>(auc, 4)> legend>(.6, .4, auc, title =>'AUC'>, cex = 1)> |
>
>
Výkon:
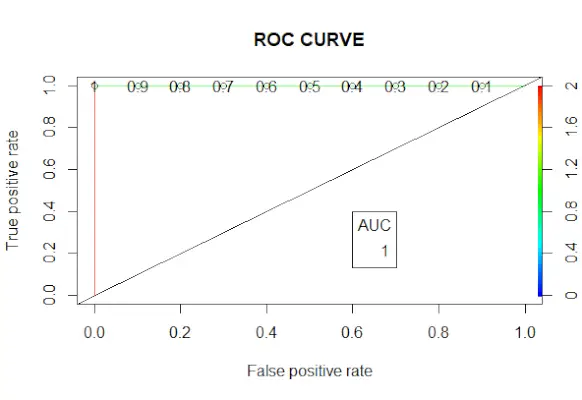
ROC krivka
Príklad 2:
Môžeme vykonať logistický regresný model Titanic Data Set v R.
R
správca powershell
modely strojového učenia
# Load the dataset> data>(Titanic)> # Convert the table to a data frame> data <->as.data.frame>(Titanic)> # Fit the logistic regression model> model <->glm>(Survived ~ Class + Sex + Age, family = binomial, data = data)> # View the summary of the model> summary>(model)> |
>
>
Výkon:
Call: glm(formula = Survived ~ Class + Sex + Age, family = binomial, data = data) Deviance Residuals: Min 1Q Median 3Q Max -1.177 -1.177 0.000 1.177 1.177 Coefficients: Estimate Std. Error z value Pr(>|z|) (Zachytenie) 4.022e-16 8.660e-01 0 1 Trieda2. -9.762e-16 1.000e+00 0 1 Trieda3. -4.699e-16 1.000e+00 0 1 TriedaPosádka -1.551.00 00 0 1 SexFemale -3.140e-16 7.071e-01 0 1 AgeAdult 5.103e-16 7.071e-01 0 1 (Parameter rozptylu pre binomickú rodinu sa považuje za 1) Nulová odchýlka: 44,361 na 44,361 stupňoch slobody Reviances: 31 na 26 stupňoch voľnosti AIC: 56,361 Počet iterácií Fisherovho skóre: 2>
Nakreslite krivku ROC pre súbor údajov Titanicu
R
# Install and load the required packages> install.packages>(>'ROCR'>)> library>(ROCR)> # Fit the logistic regression model> model <->glm>(Survived ~ Class + Sex + Age, family = binomial, data = data)> # Make predictions on the dataset> predictions <->predict>(model, type =>'response'>)> # Create a prediction object for ROCR> prediction_objects <->prediction>(predictions, titanic_df$Survived)> # Create an ROC curve object> roc_object <->performance>(prediction_obj, measure =>'tpr'>, x.measure =>'fpr'>)> # Plot the ROC curve> plot>(roc_object, main =>'ROC Curve'>, col =>'blue'>, lwd = 2)> # Add labels and a legend to the plot> legend>(>'bottomright'>, legend => >paste>(>'AUC ='>,>round>(>performance>(prediction_objects, measure =>'auc'>)> >@y.values[[1]], 2)), col =>'blue'>, lwd = 2)> |
>
>
Výkon:
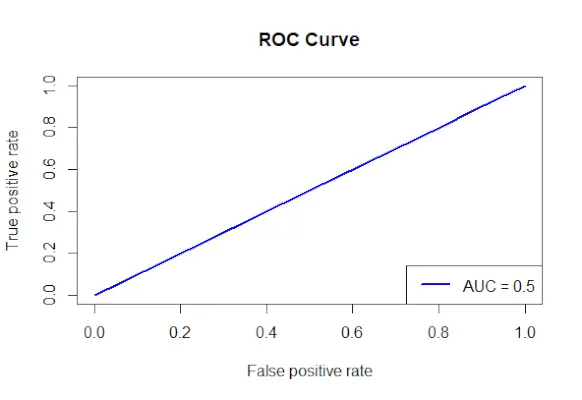
ROC krivka
- Faktory používané na predpovedanie prežitých sú špecifikované a na vytvorenie modelu logistickej regresie sa používa vzorec Trieda prežitia + pohlavie + vek.
- Pomocou funkcie predikcie () sa predpovede robia na súbore údajov pomocou prispôsobeného modelu.
- Predpokladané pravdepodobnosti sa kombinujú so skutočnými výslednými hodnotami na vytvorenie objektu predikcie pomocou metódy predpoveď() z balíka ROCR.
- Je špecifikovaná miera skutočnej pozitívnej rýchlosti (tpr) a miera osi x falošnej pozitívnej rýchlosti (fpr) a pomocou funkcie performance() z balíka ROCR sa vytvorí objekt krivky ROC.
- Objekt krivky ROC (roc_obj), ktorý určuje hlavný nadpis, farbu a šírku čiary, sa vykreslí pomocou funkcie plot().
- Používa funkciu performance() s mierou = auc na určenie hodnoty AUC (plocha pod krivkou) a do grafu pridáva štítky a legendu.
