Logistická regresia je a algoritmus strojového učenia pod dohľadom používa klasifikačné úlohy kde cieľom je predpovedať pravdepodobnosť, či inštancia patrí alebo nepatrí do danej triedy. Logistická regresia je štatistický algoritmus, ktorý analyzuje vzťah medzi dvoma dátovými faktormi. Článok skúma základy logistickej regresie, jej typy a implementácie.

Obsah

• Čo je logistická regresia?
• Logistická funkcia – sigmoidná funkcia
• Typy logistickej regresie
• Predpoklady logistickej regresie
• Ako funguje logistická regresia?
• Implementácia kódu pre logistickú regresiu
• Precision-Recall kompromis v nastavení prahu logistickej regresie
• Ako vyhodnotiť model logistickej regresie?
• Rozdiely medzi lineárnou a logistickou regresiou

Čo je logistická regresia?

Pre binárne sa používa logistická regresia klasifikácia kde používame sigmoidná funkcia , ktorý berie vstup ako nezávislé premenné a vytvára hodnotu pravdepodobnosti medzi 0 a 1.

Napríklad máme dve triedy Trieda 0 a Trieda 1, ak je hodnota logistickej funkcie pre vstup väčšia ako 0,5 (prahová hodnota), potom patrí do triedy 1, inak patrí do triedy 0. Nazýva sa regresia, pretože je rozšírením lineárna regresia ale používa sa hlavne pri klasifikačných problémoch.

Kľúčové body:

• Logistická regresia predpovedá výstup kategorickej závislej premennej. Preto musí byť výsledkom kategorická alebo diskrétna hodnota.
• Môže to byť buď áno alebo nie, 0 alebo 1, pravda alebo nepravda, atď., ale namiesto udania presnej hodnoty ako 0 a 1 udáva pravdepodobnostné hodnoty, ktoré ležia medzi 0 a 1.
• V logistickej regresii namiesto prispôsobenia regresnej čiary preložíme logistickú funkciu v tvare S, ktorá predpovedá dve maximálne hodnoty (0 alebo 1).

Logistická funkcia – sigmoidná funkcia

• Sigmoidná funkcia je matematická funkcia používaná na mapovanie predpovedaných hodnôt na pravdepodobnosti.
• Mapuje akúkoľvek skutočnú hodnotu na inú hodnotu v rozsahu 0 až 1. Hodnota logistickej regresie musí byť medzi 0 a 1, ktorá nemôže prekročiť túto hranicu, takže tvorí krivku ako tvar S.
• Krivka tvaru S sa nazýva sigmoidná funkcia alebo logistická funkcia.
• V logistickej regresii používame koncept prahovej hodnoty, ktorá definuje pravdepodobnosť buď 0 alebo 1. Napríklad hodnoty nad prahovou hodnotou majú tendenciu k 1 a hodnota pod prahovými hodnotami má tendenciu k 0.

Typy logistickej regresie

Na základe kategórií možno logistickú regresiu rozdeliť do troch typov:

1. Binomické: V binomickej logistickej regresii môžu existovať iba dva možné typy závislých premenných, ako napríklad 0 alebo 1, Pass alebo Fail atď.
2. Multinóm: V multinomiálnej logistickej regresii môžu existovať 3 alebo viac možných neusporiadaných typov závislej premennej, ako napríklad mačka, pes alebo ovca.
3. poradové číslo: V ordinálnej logistickej regresii môžu existovať 3 alebo viac možných usporiadaných typov závislých premenných, ako napríklad nízka, stredná alebo vysoká.

Predpoklady logistickej regresie

Preskúmame predpoklady logistickej regresie, pretože pochopenie týchto predpokladov je dôležité, aby sme sa uistili, že používame vhodnú aplikáciu modelu. Predpoklad zahŕňa:

1. Nezávislé pozorovania: Každé pozorovanie je nezávislé od druhého. čo znamená, že medzi vstupnými premennými neexistuje žiadna korelácia.
2. Binárne závislé premenné: Predpokladá sa, že závislá premenná musí byť binárna alebo dichotomická, čo znamená, že môže nadobúdať iba dve hodnoty. Pre viac ako dve kategórie sa používajú funkcie SoftMax.
3. Vzťah linearity medzi nezávislými premennými a logaritmickou pravdepodobnosťou: Vzťah medzi nezávislými premennými a logaritmickou pravdepodobnosťou závislej premennej by mal byť lineárny.
4. Žiadne odľahlé hodnoty: V súbore údajov by nemali byť žiadne odľahlé hodnoty.
5. Veľká veľkosť vzorky: Veľkosť vzorky je dostatočne veľká

Terminológie zapojené do logistickej regresie

Tu je niekoľko bežných pojmov súvisiacich s logistickou regresiou:

• Nezávislé premenné: Vstupné charakteristiky alebo prediktorové faktory aplikované na predpovede závislej premennej.
• Závislá premenná: Cieľová premenná v modeli logistickej regresie, ktorú sa snažíme predpovedať.
• Logistická funkcia: Vzorec používaný na vyjadrenie vzájomného vzťahu nezávislých a závislých premenných. Logistická funkcia transformuje vstupné premenné na hodnotu pravdepodobnosti medzi 0 a 1, čo predstavuje pravdepodobnosť, že závislá premenná bude 1 alebo 0.
• Šance: Je to pomer niečoho, čo sa deje, k niečomu, čo sa nevyskytuje. líši sa od pravdepodobnosti, pretože pravdepodobnosť je pomer toho, čo sa stane, ku všetkému, čo by sa mohlo vyskytnúť.
• Log-pravdepodobnosť: Log-odds, tiež známy ako logit funkcia, je prirodzený logaritmus pravdepodobnosti. V logistickej regresii sú logaritmické šance závislej premennej modelované ako lineárna kombinácia nezávislých premenných a priesečníka.
• Koeficient: Odhadované parametre modelu logistickej regresie ukazujú, ako sa nezávislé a závislé premenné navzájom týkajú.
• Zachytenie: Konštantný člen v modeli logistickej regresie, ktorý predstavuje logaritmickú pravdepodobnosť, keď sú všetky nezávislé premenné rovné nule.
• Odhad maximálnej pravdepodobnosti : Metóda použitá na odhad koeficientov modelu logistickej regresie, ktorá maximalizuje pravdepodobnosť pozorovania údajov daného modelu.

Ako funguje logistická regresia?

Logistický regresný model transformuje lineárna regresia funkcia výstup spojitej hodnoty na výstup kategorickej hodnoty pomocou sigmoidnej funkcie, ktorá mapuje akúkoľvek množinu nezávislých premenných s reálnou hodnotou na vstupe na hodnotu medzi 0 a 1. Táto funkcia je známa ako logistická funkcia.

Nech sú nezávislé vstupné funkcie:

X = egin{bmatrix} x_{11} & … & x_{1m} x_{21} & … & x_{2m} vdots & ddots & vdots x_{n1} & … & x_{nm} end{bmatrix}

a závislá premenná je Y, ktorá má iba binárnu hodnotu, t.j. 0 alebo 1.

Y = egin{cases} 0 & ext{ if } Class;1 1 & ext{ if } Class;2 end{cases}

potom aplikujte multilineárnu funkciu na vstupné premenné X.

z = left(sum_{i=1}^{n} w_{i}x_{i} ight) + b

Tux_i je i-té pozorovanie X,w_i = [w_1, w_2, w_3, cdots,w_m] sú váhy alebo koeficient a b je výraz skreslenia známy aj ako zachytenie. jednoducho to možno reprezentovať ako bodový súčin hmotnosti a skreslenia.

z = wcdot X +b

všetko, o čom sme hovorili vyššie, je lineárna regresia .

Funkcia sigmatu

Teraz používame sigmoidná funkcia kde vstupom bude z a nájdeme pravdepodobnosť medzi 0 a 1. teda predpovedané y.

sigma(z) = frac{1}{1-e^{-z}}

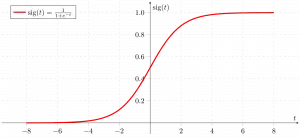
Sigmoidná funkcia

Ako je uvedené vyššie, funkcia esovitej číslice konvertuje údaje spojitej premennej na pravdepodobnosť t.j. medzi 0 a 1.

• sigma(z) smeruje k 1 asz ightarrowinfty
• sigma(z) smeruje k 0 asz ightarrow-infty
• sigma(z) je vždy ohraničená medzi 0 a 1

kde pravdepodobnosť byť triedou možno merať ako:

P(y=1) = sigma(z) P(y=0) = 1-sigma(z)

Logistická regresná rovnica

Nepárny je pomer medzi tým, čo sa niečo stane, k niečomu, čo sa nestane. líši sa od pravdepodobnosti, pretože pravdepodobnosť je pomer toho, čo sa stane, ku všetkému, čo by sa mohlo vyskytnúť. také zvláštne bude:

frac{p(x)}{1-p(x)} = e^z

Použitie prirodzeného log na nepárne. potom log nepárny bude:

egin{aligned} log left[frac{p(x)}{1-p(x)} ight] &= z log left[frac{p(x)}{1-p(x)} ight] &= wcdot X +b frac{p(x)}{1-p(x)}&= e^{wcdot X +b} ;;cdots ext{Exponentiate both sides} p(x) &=e^{wcdot X +b}cdot (1-p(x)) p(x) &=e^{wcdot X +b}-e^{wcdot X +b}cdot p(x)) p(x)+e^{wcdot X +b}cdot p(x))&=e^{wcdot X +b} p(x)(1+e^{wcdot X +b}) &=e^{wcdot X +b} p(x)&= frac{e^{wcdot X +b}}{1+e^{wcdot X +b}} end{aligned}

potom konečná logistická regresná rovnica bude:

p(X;b,w) = frac{e^{wcdot X +b}}{1+e^{wcdot X +b}} = frac{1}{1+e^{-wcdot X +b}}

Funkcia pravdepodobnosti pre logistickú regresiu

Predpokladané pravdepodobnosti budú:

• pre y=1 Predpovedané pravdepodobnosti budú: p(X;b,w) = p(x)
• pre y = 0 Predpovedané pravdepodobnosti budú: 1-p(X;b,w) = 1-p(x)

L(b,w) = prod_{i=1}^{n}p(x_i)^{y_i}(1-p(x_i))^{1-y_i}

Odoberanie prírodných kmeňov na oboch stranách

egin{aligned}log(L(b,w)) &= sum_{i=1}^{n} y_ilog p(x_i);+; (1-y_i)log(1-p(x_i)) &=sum_{i=1}^{n} y_ilog p(x_i)+log(1-p(x_i))-y_ilog(1-p(x_i)) &=sum_{i=1}^{n} log(1-p(x_i)) +sum_{i=1}^{n}y_ilog frac{p(x_i)}{1-p(x_i} &=sum_{i=1}^{n} -log1-e^{-(wcdot x_i+b)} +sum_{i=1}^{n}y_i (wcdot x_i +b) &=sum_{i=1}^{n} -log1+e^{wcdot x_i+b} +sum_{i=1}^{n}y_i (wcdot x_i +b) end{aligned}

Gradient logaritmickej pravdepodobnostnej funkcie

Aby sme našli odhady maximálnej pravdepodobnosti, rozlišujeme w.r.t w,

egin{aligned} frac{partial J(l(b,w)}{partial w_j}&=-sum_{i=n}^{n}frac{1}{1+e^{wcdot x_i+b}}e^{wcdot x_i+b} x_{ij} +sum_{i=1}^{n}y_{i}x_{ij} &=-sum_{i=n}^{n}p(x_i;b,w)x_{ij}+sum_{i=1}^{n}y_{i}x_{ij} &=sum_{i=n}^{n}(y_i -p(x_i;b,w))x_{ij} end{aligned}

Implementácia kódu pre logistickú regresiu

Binomická logistická regresia:

Cieľová premenná môže mať iba 2 možné typy: 0 alebo 1, ktoré môžu predstavovať víťazstvo vs prehra, pass vs zlyhanie, mŕtvy vs živý atď., v tomto prípade sa používajú sigmoidné funkcie, o ktorých sme už hovorili vyššie.

Import potrebných knižníc na základe požiadavky modelu. Tento kód Python ukazuje, ako použiť súbor údajov o rakovine prsníka na implementáciu modelu logistickej regresie na klasifikáciu.

Výkon :

Presnosť modelu logistickej regresie (v %): 95,6140350877193

Multinomická logistická regresia:

Cieľová premenná môže mať 3 alebo viac možných typov, ktoré nie sú usporiadané (t. j. typy nemajú kvantitatívnu významnosť), ako je choroba A verzus choroba B verzus choroba C.

V tomto prípade sa namiesto sigmoidnej funkcie použije funkcia softmax. Funkcia Softmax pre triedy K bude:

ext{softmax}(z_i) =frac{ e^{z_i}}{sum_{j=1}^{K}e^{z_{j}}}

Tu, K predstavuje počet prvkov vo vektore z a i, j iteruje cez všetky prvky vo vektore.

Potom bude pravdepodobnosť pre triedu c:

ahoj svet java

P(Y=c | overrightarrow{X}=x) = frac{e^{w_c cdot x + b_c}}{sum_{k=1}^{K}e^{w_k cdot x + b_k}}

Pri multinomickej logistickej regresii môže mať výstupná premenná viac ako dva možné samostatné výstupy . Zvážte množinu číselných údajov.

Výkon:

Presnosť modelu logistickej regresie (v %): 96,52294853963839

Ako vyhodnotiť model logistickej regresie?

Logistický regresný model môžeme vyhodnotiť pomocou nasledujúcich metrík:

• Presnosť: Presnosť poskytuje podiel správne klasifikovaných prípadov.
  Accuracy = frac{True , Positives + True , Negatives}{Total}

• presnosť: Presnosť sa zameriava na presnosť pozitívnych predpovedí.
  Precision = frac{True , Positives }{True, Positives + False , Positives}

• Odvolanie (citlivosť alebo skutočná pozitívna miera): Odvolanie meria podiel správne predpovedaných pozitívnych prípadov medzi všetkými skutočnými pozitívnymi prípadmi.
  Recall = frac{ True , Positives}{True, Positives + False , Negatives}

• Skóre F1: Skóre F1 je harmonický priemer presnosti a vybavovania.
  F1 , Score = 2 * frac{Precision * Recall}{Precision + Recall}

• Oblasť pod krivkou prevádzkovej charakteristiky prijímača (AUC-ROC): ROC krivka vykresľuje skutočnú pozitívnu mieru oproti falošnej pozitívnej miere pri rôznych prahoch. AUC-ROC meria plochu pod touto krivkou a poskytuje súhrnnú mieru výkonnosti modelu v rámci rôznych klasifikačných prahov.
• Oblasť pod krivkou presnosti vyvolania (AUC-PR): Podobne ako AUC-ROC, AUC-PR meria plochu pod krivkou presnosti a spätného vybavovania a poskytuje súhrn výkonnosti modelu v rámci rôznych kompromisov medzi presnosťou a vybavovaním.

Precision-Recall kompromis v nastavení prahu logistickej regresie

Logistická regresia sa stáva klasifikačnou technikou len vtedy, keď sa do obrazu dostane rozhodovací prah. Nastavenie prahovej hodnoty je veľmi dôležitým aspektom logistickej regresie a závisí od samotného klasifikačného problému.

Rozhodnutie o hodnote prahovej hodnoty je zásadne ovplyvnené hodnotami o presnosť a zapamätanie. V ideálnom prípade chceme, aby presnosť aj zapamätanie boli 1, ale to je zriedka.

V prípade a Presný kompromis , pri rozhodovaní o prahovej hodnote používame nasledujúce argumenty:

1. Nízka presnosť/vysoká spätná väzba: V aplikáciách, kde chceme znížiť počet falošne negatívnych výsledkov bez toho, aby sme nevyhnutne znížili počet falošných poplachov, zvolíme hodnotu rozhodnutia, ktorá má nízku hodnotu Precision alebo vysokú hodnotu Recall. Napríklad v aplikácii na diagnostiku rakoviny nechceme, aby bol žiadny postihnutý pacient klasifikovaný ako nepostihnutý bez toho, aby sme venovali veľkú pozornosť tomu, či je pacientovi nesprávne diagnostikovaná rakovina. Je to preto, že neprítomnosť rakoviny sa dá zistiť ďalšími zdravotnými ochoreniami, ale prítomnosť ochorenia sa nedá zistiť u už odmietnutého kandidáta.
2. Vysoká presnosť/nízke volanie: V aplikáciách, kde chceme znížiť počet falošne pozitívnych výsledkov bez toho, aby sme nevyhnutne znížili počet falošných negatív, zvolíme hodnotu rozhodnutia, ktorá má vysokú hodnotu Precision alebo nízku hodnotu Recall. Ak napríklad klasifikujeme zákazníkov, či budú na personalizovanú reklamu reagovať pozitívne alebo negatívne, chceme si byť úplne istí, že zákazník na reklamu zareaguje pozitívne, pretože v opačnom prípade môže negatívna reakcia spôsobiť stratu potenciálneho predaja zákazníka.

Rozdiely medzi lineárnou a logistickou regresiou

Rozdiel medzi lineárnou regresiou a logistickou regresiou je v tom, že výstup lineárnej regresie je nepretržitá hodnota, ktorá môže byť čokoľvek, zatiaľ čo logistická regresia predpovedá pravdepodobnosť, že inštancia patrí do danej triedy alebo nie.

Logistická regresia – často kladené otázky (FAQ)

Čo je logistická regresia v strojovom učení?

Logistická regresia je štatistická metóda na vývoj modelov strojového učenia s binárnymi závislými premennými, t. j. binárnymi. Logistická regresia je štatistická technika používaná na opis údajov a vzťahu medzi jednou závislou premennou a jednou alebo viacerými nezávislými premennými.

Aké sú tri typy logistickej regresie?

Logistická regresia je rozdelená do troch typov: binárna, multinomická a ordinálna. Líšia sa prevedením aj teóriou. Binárna regresia sa týka dvoch možných výsledkov: áno alebo nie. Multinomická logistická regresia sa používa, ak existujú tri alebo viac hodnôt.

Prečo sa na klasifikačný problém používa logistická regresia?

Logistická regresia sa ľahšie implementuje, interpretuje a trénuje. Veľmi rýchlo klasifikuje neznáme záznamy. Keď je množina údajov lineárne oddeliteľná, funguje dobre. Koeficienty modelu možno interpretovať ako ukazovatele dôležitosti funkcie.

Čo odlišuje logistickú regresiu od lineárnej regresie?

Zatiaľ čo lineárna regresia sa používa na predpovedanie kontinuálnych výsledkov, logistická regresia sa používa na predpovedanie pravdepodobnosti, že pozorovanie spadá do špecifickej kategórie. Logistická regresia využíva logistickú funkciu v tvare S na mapovanie predpokladaných hodnôt medzi 0 a 1.

Akú úlohu zohráva logistická funkcia v logistickej regresii?

Logistická regresia sa spolieha na logistickú funkciu na premenu výstupu na skóre pravdepodobnosti. Toto skóre predstavuje pravdepodobnosť, že pozorovanie patrí do konkrétnej triedy. Krivka v tvare S pomáha pri prahovaní a kategorizácii údajov do binárnych výstupov.