Lineárna regresia a logistická regresia sú dva známe algoritmy strojového učenia, ktoré spadajú pod techniku učenia pod dohľadom. Keďže oba algoritmy sú svojou povahou kontrolované, tieto algoritmy používajú na predpovede označený súbor údajov. Ale hlavný rozdiel medzi nimi je v tom, ako sa používajú. Lineárna regresia sa používa na riešenie regresných problémov, zatiaľ čo logistická regresia sa používa na riešenie klasifikačných problémov. Popis oboch algoritmov je uvedený nižšie spolu s tabuľkou rozdielov.
Lineárna regresia:
- Lineárna regresia je jedným z najjednoduchších algoritmov strojového učenia, ktorý spadá pod techniku supervízneho učenia a používa sa na riešenie regresných problémov.
- Používa sa na predikciu spojitej závislej premennej pomocou nezávislých premenných.
- Cieľom lineárnej regresie je nájsť najvhodnejšiu líniu, ktorá dokáže presne predpovedať výstup pre spojitú závislú premennú.
- Ak sa na predikciu používa jedna nezávislá premenná, potom sa nazýva jednoduchá lineárna regresia a ak existuje viac ako dve nezávislé premenné, potom sa takáto regresia nazýva viacnásobná lineárna regresia.
- Nájdením najvhodnejšej čiary algoritmus vytvorí vzťah medzi závislou premennou a nezávislou premennou. A vzťah by mal mať lineárny charakter.
- Výstupom pre lineárnu regresiu by mali byť iba spojité hodnoty ako cena, vek, plat atď. Vzťah medzi závislou premennou a nezávislou premennou je možné zobraziť na obrázku nižšie:

Na obrázku vyššie je závislá premenná na osi Y (plat) a nezávislá premenná je na osi x (skúsenosť). Regresná čiara môže byť napísaná ako:
y= a<sub>0</sub>+a<sub>1</sub>x+ ε
Kde0a a1sú koeficienty a ε je chybový člen.
Logistická regresia:
- Logistická regresia je jedným z najpopulárnejších algoritmov strojového učenia, ktoré spadajú pod techniky supervízneho učenia.
- Dá sa použiť na klasifikáciu ako aj na regresné problémy, ale hlavne na klasifikačné problémy.
- Logistická regresia sa používa na predpovedanie kategorickej závislej premennej pomocou nezávislých premenných.
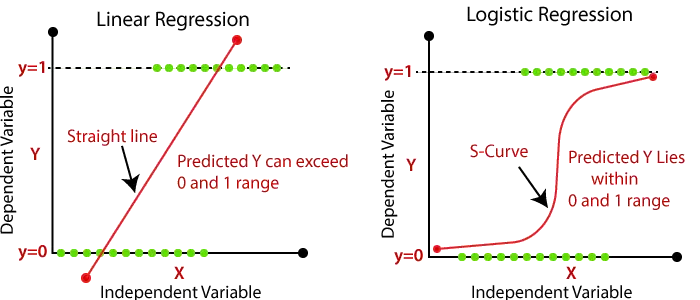
- Výstup problému logistickej regresie môže byť iba medzi 0 a 1.
- Logistická regresia sa môže použiť tam, kde sa vyžadujú pravdepodobnosti medzi dvoma triedami. Napríklad, či bude dnes pršať alebo nie, buď 0 alebo 1, pravda alebo nepravda atď.
- Logistická regresia je založená na koncepte odhadu maximálnej pravdepodobnosti. Podľa tohto odhadu by mali byť pozorované údaje najpravdepodobnejšie.
- Pri logistickej regresii prechádzame váženým súčtom vstupov cez aktivačnú funkciu, ktorá dokáže mapovať hodnoty medzi 0 a 1. Takáto aktivačná funkcia je známa ako sigmoidná funkcia a získaná krivka sa nazýva sigmoidná krivka alebo S-krivka. Zvážte nasledujúci obrázok:

- Rovnica pre logistickú regresiu je:

Rozdiel medzi lineárnou regresiou a logistickou regresiou:
| Lineárna regresia | Logistická regresia |
|---|---|
| Lineárna regresia sa používa na predpovedanie spojitej závislej premennej pomocou daného súboru nezávislých premenných. | Logistická regresia sa používa na predpovedanie kategorickej závislej premennej pomocou daného súboru nezávislých premenných. |
| Lineárna regresia sa používa na riešenie problému regresie. | Logistická regresia sa používa na riešenie klasifikačných problémov. |
| V Lineárnej regresii predpovedáme hodnotu spojitých premenných. | V logistickej regresii predikujeme hodnoty kategorických premenných. |
| Pri lineárnej regresii nájdeme najvhodnejšiu líniu, pomocou ktorej môžeme ľahko predpovedať výstup. | V Logistic Regression nájdeme S-krivku, podľa ktorej môžeme klasifikovať vzorky. |
| Na odhad presnosti sa používa metóda odhadu najmenších štvorcov. | Na odhad presnosti sa používa metóda odhadu maximálnej pravdepodobnosti. |
| Výstupom pre lineárnu regresiu musí byť spojitá hodnota, ako je cena, vek atď. | Výstupom logistickej regresie musí byť kategorická hodnota, napríklad 0 alebo 1, áno alebo nie atď. |
| Pri lineárnej regresii sa vyžaduje, aby vzťah medzi závislou premennou a nezávislou premennou bol lineárny. | Pri logistickej regresii sa nevyžaduje lineárny vzťah medzi závislou a nezávislou premennou. |
| Pri lineárnej regresii môže existovať kolinearita medzi nezávislými premennými. | Pri logistickej regresii by medzi nezávislou premennou nemala existovať kolinearita. |
