Lineárne programovanie je matematický koncept, ktorý sa používa na nájdenie optimálneho riešenia lineárnej funkcie. Táto metóda využíva jednoduché predpoklady na optimalizáciu danej funkcie. Lineárne programovanie má obrovské uplatnenie v reálnom svete a používa sa na riešenie rôznych typov problémov.
Lineárne programovanie sa používa v rôznych priemyselných odvetviach, ako je lodný priemysel, výrobný priemysel, dopravný priemysel, telekomunikácie a iné.
Termín lineárne programovanie sa skladá z dvoch slov lineárne a programovanie, slovo lineárne hovorí o vzťahu medzi rôznymi typmi premenných prvého stupňa použitých v probléme a slovo programovanie nám hovorí o postupnom riešení týchto problémov.
V tomto článku sa podrobne dozvieme o lineárnom programovaní, jeho príkladoch, vzorcoch a iných konceptoch.
Obsah
- Čo je lineárne programovanie?
- Komponenty lineárneho programovania
- Príklady lineárneho programovania
- Problémy lineárneho programovania
- Typy problémov lineárneho programovania
- Vzorec lineárneho programovania
- Ako vyriešiť problémy s lineárnym programovaním?
- Metódy lineárneho programovania
- Simplexná metóda lineárneho programovania
- Grafická metóda lineárneho programovania
- Aplikácie lineárneho programovania
- Význam lineárneho programovania
- Aktuálne aplikácie lineárneho programovania
- Lineárne programovanie v operačnom výskume
- Simplexná metóda
Čo je lineárne programovanie?
Lineárne programovanie alebo Lineárna optimalizácia je technika, ktorá nám pomáha nájsť optimálne riešenie pre daný problém, optimálne riešenie je riešenie, ktoré je najlepším možným výsledkom daného konkrétneho problému.
Jednoducho povedané, je to metóda, ako zistiť, ako niečo urobiť čo najlepšie. S obmedzenými zdrojmi musíte optimálne využívať zdroje a dosiahnuť najlepší možný výsledok v konkrétnom cieli, ako sú najnižšie náklady, najvyššia marža alebo najmenej času.
Situácia, ktorá si vyžaduje hľadanie najlepších hodnôt premenných podliehajúcich určitým obmedzeniam, je situácia, keď používame problémy lineárneho programovania. Tieto situácie sa nedajú zvládnuť bežným kalkulom a numerickými technikami.
Definícia lineárneho programovania
Lineárne programovanie je technika používaná na optimalizáciu konkrétneho scenára. Použitie lineárneho programovania nám poskytuje najlepší možný výsledok v danej situácii. Využíva všetky dostupné zdroje takým spôsobom, aby dosiahli optimálny výsledok.
Komponenty lineárneho programovania
Základné zložky problému lineárneho programovania (LP) sú:
- Rozhodovacie premenné: Premenné, ktoré chcete určiť, aby ste dosiahli optimálne riešenie.
- Objektívna funkcia: M atematická rovnica, ktorá predstavuje cieľ, ktorý chcete dosiahnuť
- Obmedzenia: Obmedzenia alebo obmedzenia, ktoré musia dodržiavať vaše premenné rozhodovania.
- Negatívne obmedzenia: V niektorých scenáre reálneho sveta, rozhodovacie premenné nemôžu byť negatívne
Ďalšie charakteristiky lineárneho programovania
- konečnosť: Počet rozhodovacích premenných a obmedzení v probléme LP je konečný.
- Linearita: Cieľovou funkciou a všetkými obmedzeniami musia byť lineárne funkcie rozhodovacích premenných . Znamená to, že stupeň premenných by mal byť jeden.
Príklady lineárneho programovania
Situácie, v ktorých sa lineárne programovanie používa, môžeme pochopiť pomocou príkladu uvedeného nižšie,
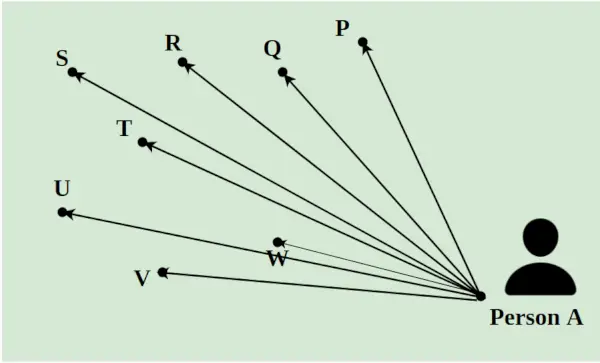
Predpokladajme, že doručovateľ musí doručiť 8 balíkov za deň na rôzne miesta v meste. Musí vybrať všetky pakety z A a doručiť ich do bodov P, Q, R, S, T, U, V a W. Vzdialenosť medzi nimi je vyznačená pomocou čiar, ako je znázornené na obrázku nižšie. Najkratšia cesta, ktorú doručovateľ sleduje, je vypočítaná pomocou konceptu lineárneho programovania.
program dvojrozmerného poľa v c
Problémy lineárneho programovania
Problémy lineárneho programovania (LPP) zahŕňajú optimalizáciu lineárnej funkcie s cieľom nájsť riešenie optimálnej hodnoty pre funkciu. Optimálna hodnota môže byť maximálna alebo minimálna hodnota.
V LPP sa nazývajú lineárne funkcie objektívne funkcie. Objektívna funkcia môže mať viacero premenných, ktoré podliehajú podmienkam a musia ich spĺňať lineárne obmedzenia .
Typy problémov lineárneho programovania
Existuje mnoho rôznych problémov lineárneho programovania (LPP), ale v tomto článku sa budeme zaoberať tromi hlavnými problémami lineárneho programovania.
Výrobné problémy
Výrobné problémy sú problémom, ktorý sa zaoberá počtom jednotiek, ktoré by sa mali vyrobiť alebo predať, aby sa maximalizovali zisky, keď každý výrobok vyžaduje stálu pracovnú silu, strojové hodiny a suroviny.
Problémy s diétou
Používa sa na výpočet počtu rôznych druhov zložiek, ktoré sa majú zahrnúť do stravy, aby sa dosiahli minimálne náklady, v závislosti od dostupnosti potravín a ich cien.
Dopravné problémy
Používa sa na určenie harmonogramu prepravy s cieľom nájsť najlacnejší spôsob prepravy produktu zo závodov/tovární na rôznych miestach na rôzne trhy.
Vzorec lineárneho programovania
Problém lineárneho programovania pozostáva z:
- Rozhodovacie premenné
- Objektívna funkcia
- Obmedzenia
- Negatívne obmedzenia
Rozhodovacie premenné sú premenné x a y, ktoré rozhodujú o výstupe úlohy lineárneho programovania a predstavujú konečné riešenie.
The objektívna funkcia , vo všeobecnosti reprezentovaná Z, je lineárna funkcia, ktorú je potrebné optimalizovať podľa danej podmienky, aby sa získalo konečné riešenie.
The obmedzenia uložené rozhodovacím premenným, ktoré obmedzujú ich hodnoty, sa nazývajú obmedzenia.
Všeobecný vzorec problému lineárneho programovania je,
Objektívna funkcia : Z = ax + by
Obmedzenia: cx + dy ≥ e, px + qy ≤ r
Nezáporné obmedzenia: x ≥ 0, y ≥ 0
Vo vyššie uvedenej podmienke sú x a y rozhodovacie premenné.
Ako vyriešiť problémy s lineárnym programovaním?
Pred riešením úloh lineárneho programovania musíme najprv sformulovať úlohy podľa štandardných parametrov. Kroky na riešenie problémov lineárneho programovania sú:
Krok 1: Označte v úlohe rozhodovacie premenné.
Krok 2: Zostavte objektívnu funkciu problému a skontrolujte, či je potrebné funkciu minimalizovať alebo maximalizovať.
Krok 3: Napíšte všetky obmedzenia lineárnych problémov.
Krok 4: Zabezpečte nezáporné obmedzenia rozhodovacích premenných.
Krok 5: Teraz vyriešte problém lineárneho programovania pomocou akejkoľvek metódy, vo všeobecnosti používame buď simplexnú alebo grafickú metódu.
Metódy lineárneho programovania
Na riešenie problémov lineárneho programovania používame rôzne metódy. Dve najbežnejšie používané metódy sú,
- Simplexná metóda
- Grafická metóda
Dozvieme sa podrobne o týchto dvoch metódach v tomto článku,
Simplexná metóda lineárneho programovania
Jednou z najbežnejších metód riešenia problému lineárneho programovania je simplexná metóda. V tejto metóde opakujeme špecifickú podmienku „n“ niekoľkokrát, kým sa nedosiahne optimálne riešenie.
Kroky potrebné na riešenie problémov lineárneho programovania pomocou simplexnej metódy sú:
Krok 1: Formulujte úlohy lineárneho programovania na základe daných obmedzení.
Krok 2: Preveďte všetky dané nerovnosti na rovnice alebo rovnosti problémov lineárneho programovania pridaním premennej slack ku každej nerovnosti tam, kde je to potrebné.
Krok 3: Zostavte počiatočnú simplexnú tabuľku. Reprezentáciou každej obmedzujúcej rovnice v riadku a napísaním cieľovej funkcie v spodnom riadku. Takto získaná tabuľka sa nazýva Simplexová tabuľka.
Krok 4: Identifikujte najväčší záporný záznam v spodnom riadku, stĺpec prvku s najvyšším záporným záznamom sa nazýva pivotový stĺpec
Krok 5: Rozdeľte položky pravého stĺpca so záznamami príslušného kľúčového stĺpca s výnimkou záznamov v najspodnejšom riadku. Teraz sa riadok, ktorý obsahuje najmenej položiek, nazýva hlavný riadok. Otočný prvok sa získa priesečníkom otočného radu a otočného stĺpika.
Krok 6: Pomocou maticovej operácie a pomocou prvku pivot urobte všetky záznamy v stĺpci pivot na nulu.
Krok 7: Skontrolujte nezáporné položky v najspodnejšom riadku, ak v spodnom riadku nie sú žiadne záporné položky, ukončite proces, inak začnite proces znova od kroku 4.
Krok 8: Takto získaná konečná simplexná tabuľka poskytuje riešenie nášho problému.
Grafická metóda lineárneho programovania
Grafická metóda je iná metóda ako Simplexová metóda, ktorá sa používa na riešenie problémov lineárneho programovania. Ako už názov napovedá, táto metóda využíva grafy na riešenie daných problémov lineárneho programovania. Toto je najlepšia metóda na riešenie problémov lineárneho programovania a vyžaduje menej úsilia ako simplexná metóda.
Pri použití tejto metódy vykreslíme všetky nerovnosti, ktoré sú vystavené obmedzeniam v daných úlohách lineárneho programovania. Akonáhle sú všetky nerovnosti daného LPP vynesené do XY grafu, spoločná oblasť všetkých nerovností dáva optimálne riešenie. Vypočítajú sa všetky rohové body realizovateľnej oblasti a vypočíta sa hodnota účelovej funkcie vo všetkých týchto bodoch, potom porovnaním týchto hodnôt dostaneme optimálne riešenie LPP.
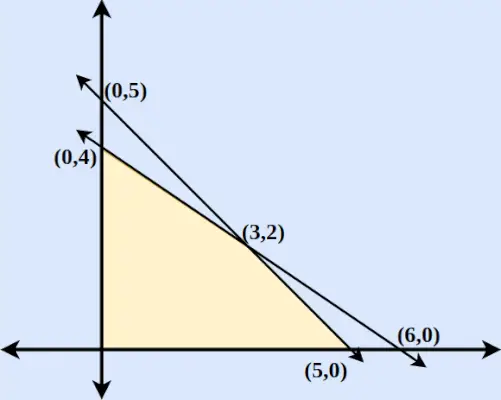
Príklad: Nájdite maximálnu a minimálnu hodnotu z = 6x + 9y, keď sú obmedzujúce podmienky,
- 2x + 3r ≤ 12
- x a y> 0
- x + y ≤ 5
Riešenie:
Krok 1 : Najprv preveďte nerovnice na normálne rovnice. Rovnice teda budú 2x+3y = 0, x = 0, y = 0 a x + y = 5.
Krok 2 : Nájdite body, v ktorých 2x + 3y a x + y = 5 pretínajú os x a os y. Ak chcete nájsť priesečník osi x, vložte y = 0 do príslušnej rovnice a nájdite bod. Podobne pre priesečníky osi y vložte x = 0 do príslušnej rovnice.
Krok 3 : Nakreslite dve čiary pretínajúce os x a os y. Zistili sme, že dve osi sa navzájom pretínajú v (3,2).
Krok 4 : Pre x ≥ 0 a y ≥ 0 zistíme, že sú dodržané obe nerovnice. Oblasť teda bude zahŕňať oblasť oblasti ohraničenú dvoma osami a obe čiary zahŕňajúce začiatok. Vykreslená oblasť je znázornená nižšie na obrázku.
Krok 5 : Nájdite Z pre každý bod a maximá a minimá.
Súradnice Z = 6x + 9r (0,5) Z = 45 (0,4) Z = 36 (5,0) Z = 30 (6,0) Z = 36 (3.2) Z = 36 Zistili sme teda, že Z = 6x + 9y je maximum pri (0,5) a minimum pri (5,0).
Aplikácie lineárneho programovania
Lineárne programovanie má uplatnenie v rôznych oblastiach. Používa sa na nájdenie minimálnych nákladov na proces, keď sú dané všetky obmedzenia problémov. Používa sa na optimalizáciu nákladov na dopravu vozidla atď. Lineárne programovanie má rôzne aplikácie
Strojársky priemysel
Engineering Industries používa lineárne programovanie na riešenie konštrukčných a výrobných problémov a na získanie maximálneho výkonu z daného stavu.
Výrobné odvetvia
Výrobný priemysel používa lineárne programovanie na maximalizáciu zisku spoločností a na zníženie výrobných nákladov.
Energetický priemysel
Energetické spoločnosti využívajú lineárne programovanie na optimalizáciu svojho výrobného výkonu.
Dopravný priemysel
Lineárne programovanie sa používa aj v dopravnom priemysle na nájdenie cesty, ako minimalizovať náklady na dopravu.
Význam lineárneho programovania
Lineárne programovanie má obrovský význam v rôznych priemyselných odvetviach, pretože maximalizuje výstupnú hodnotu a zároveň minimalizuje vstupné hodnoty podľa rôznych obmedzení.
LP je vysoko použiteľné, keď máme pri riešení problému viacero podmienok a musíme výstup problému optimalizovať, t. j. buď musíme nájsť minimálnu alebo maximálnu hodnotu podľa danej podmienky.
Čítaj viac,
- Lineárne nerovnosti
- Algebraické riešenie lineárnych nerovníc
Problémy lineárneho programovania
Problém 1: Spoločnosť vyrába a predáva dva typy produktov a výrobné náklady každej jednotky a a b sú 200 rupií a 150 rupií, každá jednotka produktu prináša zisk 20 rupií a každá jednotka produktu b prináša zisk 15 rupií pri predaji. . Spoločnosť odhaduje, že mesačný dopyt po produktoch A a B bude maximálne na úrovni zozbieranej jednotky v celom produkčnom rozpočte na mesiac je stanovený na 50 000 rupií. Koľko jednotiek by mala spoločnosť vyrobiť, aby dosiahla maximálny zisk z mesačného predaja a b?
Riešenie:
normálne formy
Nech x = počet jednotiek typu A
y = počet jednotiek typu B
Maximalizovať Z = 40x + 50r
S výhradou obmedzení
3x + y ≤ 9
x + 2y ≤ 8
a x, y> 0
Zvážte rovnicu,
3x + y = 9
x = 3
y = 0
a x + 2y = 8
x = 8
y = 0
Teraz môžeme určiť maximálnu hodnotu Z vyhodnotením hodnoty Z v štyroch bodoch (vrcholoch), ktoré sú uvedené nižšie
Vertices
Z = 40x + 50r
(0, 0)
Z = 40 x 0 + 50 x 0 = Rs. 0
(3, 0)
Z = 40 x 3 + 50 x 0 = Rs. 120
(0, 4)
Z = 40 x 0 + 50 x 4 = Rs. 200
(23)
Z = 40 x 2 + 50 x 3 = Rs. 230
Maximálny zisk, Z = Rs. 230
∴ Počet jednotiek typu A je 2 a počet jednotiek typu B je 3.
Úloha 2: Maximalizujte Z = 3x + 4r.
S výhradou obmedzení x + y ≤ 450, 2x + y ≤ 600 a x, y ≤ 0.
Riešenie:
Máme z daného
Obmedzenia (1)
X + Y = 450
Uvedenie x = 0, ⇒ 0 + y = 450 ⇒ y = 450
Uvedenie y = 0, ⇒ x + 0 = 450 ⇒ x = 450
od, Obmedzenia (2)
2x + y = 600
Uvedenie x = 0, ⇒ 0 + y = 600 ⇒ y = 600
Vloženie y = 0, ⇒ 2x + 0 = 600 ⇒ x = 300
Teraz máme súradnicu bodov Z = 3x + 4y
| Vertices | Z = 3x + 4r |
|---|---|
| (0, 0) | Z = 3 × 0 + 4 × 0 = 0 |
| (300, 0) | Z = 3 × 300 + 4 × 0 = 900 |
| (150, 300) | Z = 3 × 150 + 4 × 300 = 1650 |
| (0, 450) | Z = 3 × 0 + 4 × 450 = 1800 |
Preto je optimálne riešenie maximum Z = 1800 pri súradnici x = 0 a y = 450. Graf je uvedený nižšie.

Aktuálne aplikácie lineárneho programovania
Lineárne programovanie, výkonná matematická technika, sa používa na riešenie optimalizačných problémov v rôznych priemyselných odvetviach. Tu sú niektoré moderné aplikácie:
- Optimalizácia dodávateľského reťazca : Lineárne programovanie pomáha spoločnostiam minimalizovať náklady a maximalizovať efektivitu v ich dodávateľských reťazcoch. Používa sa na určenie nákladovo najefektívnejších dopravných trás, skladových operácií a stratégií riadenia zásob.
- Energetický manažment : V energetickom sektore sa na optimalizáciu kombinácie metód výroby energie využíva lineárne programovanie. To zahŕňa vyváženie tradičných zdrojov energie s obnoviteľnými, aby sa znížili náklady a dopad na životné prostredie a zároveň sa uspokojil dopyt.
- Návrh telekomunikačnej siete : Lineárne programovanie pomáha pri navrhovaní efektívnych telekomunikačných sietí. Pomáha pri prideľovaní šírky pásma, navrhovaní rozloženia siete a optimalizácii toku dát, aby sa zabezpečila vysokorýchlostná komunikácia pri nižších nákladoch.
- Finančné plánovanie : Firmy a finanční analytici používajú lineárne programovanie na optimalizáciu portfólia, riadenie rizík a kapitálové rozpočtovanie. Pomáha pri investičných rozhodnutiach, ktoré maximalizujú výnosy a zároveň minimalizujú riziko.
- Logistika zdravotnej starostlivosti : V zdravotníctve sa lineárne programovanie používa na optimalizáciu prideľovania zdrojov, ako sú nemocničné lôžka, zdravotnícky personál a vybavenie. Je to kľúčové pre zlepšenie starostlivosti o pacientov, skrátenie čakacích dôb a efektívne riadenie nákladov.
- Optimalizácia výrobného procesu : Lineárne programovanie sa používa na určenie optimálnych úrovní výroby pre viacero produktov vo výrobnom závode, pričom sa zohľadňujú obmedzenia, akými sú práca, materiály a dostupnosť strojov.
- Poľnohospodárske plánovanie : Farmári a poľnohospodárski plánovači používajú lineárne programovanie na rozhodovanie o výbere plodín, využívaní pôdy a prideľovaní zdrojov, aby maximalizovali výnosy a zisky a zároveň šetrili zdroje.
- Plánovanie posádky leteckej spoločnosti : Letecké spoločnosti využívajú lineárne programovanie na efektívne plánovanie posádok, čím sa zabezpečuje, že personál letov je v súlade s predpismi a minimalizujú sa prevádzkové náklady.
Tieto aplikácie demonštrujú všestrannosť a silu lineárneho programovania pri riešení zložitých optimalizačných problémov v rôznych sektoroch, čím dokazujú jeho význam v dnešnom svete založenom na údajoch.
Lineárne programovanie v operačnom výskume
- Základný nástroj : Lineárne programovanie je základným nástrojom operačného výskumu na optimalizáciu zdrojov.
- Rozhodovanie : Pomáha pri prijímaní najlepších rozhodnutí týkajúcich sa alokácie zdrojov, maximalizácie zisku alebo minimalizácie nákladov.
- Široké aplikácie : Používa sa v rôznych oblastiach, ako je logistika, výroba, financie a zdravotníctvo na riešenie zložitých problémov.
- Modelovanie problémov skutočného sveta : Transformuje problémy zo skutočného sveta do matematických modelov s cieľom nájsť najefektívnejšie riešenia.
Simplexná metóda
- Optimalizačný algoritmus : Simplexová metóda je výkonný algoritmus používaný v lineárnom programovaní na nájdenie optimálneho riešenia lineárnych nerovností.
- Prístup krok za krokom : Iteratívne sa posúva smerom k najlepšiemu riešeniu navigáciou po okrajoch realizovateľnej oblasti definovanej obmedzeniami.
- Efektívnosť : Známy svojou efektívnosťou pri riešení rozsiahlych problémov lineárneho programovania.
- Všestrannosť : Použiteľné v rôznych oblastiach, ako je plánovanie stravovania, sieťové toky, plánovanie výroby a ďalšie, čím sa ukazuje jeho všestrannosť.
Lineárne programovanie – často kladené otázky
Čo je lineárne programovanie?
Lineárne programovanie je matematický koncept, ktorý sa používa na optimalizáciu daného lineárneho problému, ktorý má rôzne obmedzenia. Pomocou lineárneho programovania dosiahneme optimálny výstup daného problému
Aké sú problémy lineárneho programovania?
Problémy lineárneho programovania (LPP) sú problémy, ktoré poskytujú optimálne riešenie daných podmienok.
Čo je vzorec lineárneho programovania?
Všeobecné vzorce lineárneho programovania sú,
- Účelová funkcia: Z = ax + by
- Obmedzenia: px + qy ≤ r, sx + ty ≤ u
- Negatívne obmedzenia: x ≥ 0, y ≥ 0
Aké sú rôzne typy lineárneho programovania?
Rôzne typy metód lineárneho programovania sú napr.
- Lineárne programovanie simplexnou metódou
- Lineárne programovanie metódou R
- Lineárne programovanie grafickou metódou
Aké sú požiadavky na lineárne programovanie?
Rôzne požiadavky na problémy lineárneho programovania sú,
- Linearita
- Objektívna funkcia
- Obmedzenia
- Negatívnosť
Aké sú výhody lineárneho programovania?
Rôzne výhody lineárneho programovania sú,
- Poskytuje optimálne riešenie akéhokoľvek daného lineárneho problému.
- Je ľahko použiteľný a vždy poskytuje konzistentné výsledky
- Pomáha maximalizovať zisky a znižovať vstupné náklady.