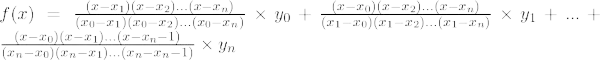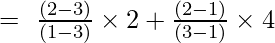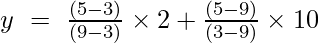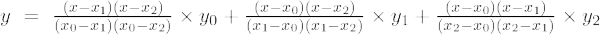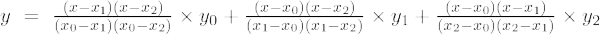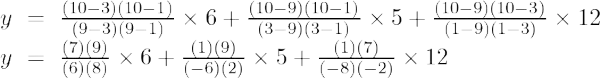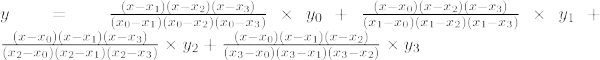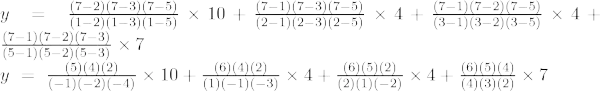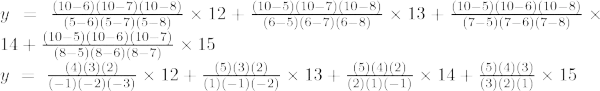LAGRANGEOV VZOREC INTERPOLÁCIE: DÔKAZ, PRÍKLADY A ČASTO KLADENÉ OTÁZKY

Lagrangeov interpolačný vzorec nájde polynóm nazývaný Lagrangeov polynóm, ktorý nadobúda určité hodnoty v ľubovoľnom bode. Je to n-tý stupeňpolynomické vyjadrenie funkcie f(x). Metóda interpolácie sa používa na nájdenie nových dátových bodov v rozsahu diskrétnej množiny známych dátových bodov.

V tomto článku sa podrobne dozvieme o Lagrangeovej interpolácii, Lagrangeovom interpolačnom vzorci, dôkaze pre Lagrangeov interpolačný vzorec, príkladoch založených na Lagrangeovom interpolačnom vzorci a ďalších.

Čo je Lagrangeova interpolácia?

Lagrangeova interpolácia je spôsob, ako nájsť hodnotu akejkoľvek funkcie v akomkoľvek danom bode, keď funkcia nie je daná. Na získanie hodnoty funkcie v ľubovoľnom požadovanom bode používame ďalšie body funkcie.

Predpokladajme, že máme funkciu y = f(x), v ktorej dosadením hodnôt x získame rôzne hodnoty y. A dostávame dva body (x₁, a₁) a (x₂, a₂) na krivke sa potom hodnota y pri x = a (konštanta) vypočíta pomocou Lagrangeovho interpolačného vzorca.

Lagrangeov interpolačný vzorec

Vzhľadom na niekoľko reálnych hodnôt x₁, X₂, X₃, …, X_na y₁, a₂, a₃, … a_na bude existovať polynóm P s reálnymi koeficientmi spĺňajúcimi podmienky P(x_i) = a_i, ∀ i = {1, 2, 3, …, n} a stupeň polynómu P musí byť menší ako počet reálnych hodnôt, t. j. stupeň (P)

Lagrangeov interpolačný vzorec pre n-tý rád

Vzorec Lagrangeovej interpolácie pre n^thpolynóm stupňa je uvedený nižšie:

Lagrangeov interpolačný vzorec pre n ^th objednávka je,

$f(x)=frac{(x-x_1)(x-x_2)...(x-x_n)}{(x_0-x_1)(x_0-x_2)...(x_0-x_n)}krát y_0+ frac{(x-x_0)(x-x_2)...(x-x_n)}{(x_1-x_0)(x_1-x_2)...(x_1-x_n)}krát y_1+...+ frac{(x-x_0)(x-x_1)...(x-x_n-1)}{(x_n-x_0)(x_n-x_1)...(x_n-x_n-1)}krát y_n$

Lagrangeov vzorec interpolácie prvého rádu

AkStupeň polynómu je 1, potom sa nazýva polynóm prvého rádu. Lagrangeov interpolačný vzorec pre 1^svrádové polynómy je,

$f(x)~=~frac{(x-x_1)}{(x_0-x_1)}krát y_0+frac{(x-x_0)}{(x_1-x_0)}krát y_1$

Lagrangeov vzorec interpolácie druhého rádu

Ak je stupeň polynómu 2, potom sa nazýva polynóm druhého rádu. Lagrangeov interpolačný vzorec pre polynómy 2. rádu je,

$f(x)~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}krát y_0+frac{(x-x_0)(x-x_2)} {(x_1-x_0)(x_1-x_2)}krát y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}krát y_2$

Dôkaz Lagrangeovej vety

Uvažujme polynóm n-tého stupňa daného tvaru,

f(x) = A₀(x – x₁) (x – x₂) (x – x₃)…(x – x_n) + A₁(x – x₁) (x – x₂) (x – x₃)…(x – x_n) + … + A_(n-1)(x – x₁) (x – x₂) (x – x₃)…(x – x_n)

Náhradné pozorovania x_izískať A_i

Dajte x = x₀potom dostaneme A₀

binárny strom

f(x₀) = a₀= A₀(X₀- X₁)(X₀- X₂)(X₀- X₃)…(X₀- X_n)

A ₀ = a ₀ /(X ₀ - X ₁ )(X ₀ - X ₂ )(X ₀ - X ₃ )…(X ₀ - X _n )

Dosadením x = x₁dostaneme A₁

f(x₁) = a₁= A₁(X₁- X₀)(X₁- X₂)(X₁- X₃)…(X₁- X_n)

A ₁ = a ₁ /(X ₁ - X ₀ )(X ₁ - X ₂ )(X ₁ - X ₃ )…(X ₁ - X _n )

Podobne dosadením x = x_ndostaneme A_n

f(x_n) = a_n= A_n(X_n- X₀)(X_n- X₁)(X_n- X₂)…(X_n- X_n-1)

A _n = a _n /(X _n - X ₀ )(X _n - X ₁ )(X _n - X ₂ )…(X _n - X _n-1 )

Ak dosadíme všetky hodnoty A_ivo funkcii f(x), kde i = 1, 2, 3, …n potom dostaneme vzorec Lagrangeovej interpolácie ako,

$f(x)~=~frac{(x-x_1)(x-x_2)...(x-x_n)}{(x_0-x_1)(x_0-x_2)...(x_0-x_n)} krát y_0+frac{(x-x_0)(x-x_2)...(x-x_n)}{(x_1-x_0)(x_1-x_2)...(x_1-x_n)}krát y_1+... +frac{(x-x_0)(x-x_1)...(x-x_n-1)}{(x_n-x_0)(x_n-x_1)...(x_n-x_n-1)}krát y_n$

Vlastnosti Lagrangeovho interpolačného vzorca

Rôzne vlastnosti Lagrangeovho interpolačného vzorca sú diskutované nižšie,

Tento vzorec sa používa na nájdenie hodnoty funkcie v akomkoľvek bode, aj keď samotná funkcia nie je zadaná.
Používa sa aj vtedy, ak uvedené body nie sú rovnomerne rozmiestnené.
Udáva hodnotu závislej premennej pre ľubovoľnú nezávislú premennú patriacu do ktorejkoľvek funkcie, a preto sa používa v numerickej analýze na nájdenie hodnôt funkcie atď.

Použitie Lagrangeovho interpolačného vzorca

Rôzne použitia Lagrangeovho interpolačného vzorca sú diskutované nižšie,

Používa sa na nájdenie hodnoty závislej premennej pri akejkoľvek konkrétnej nezávislej premennej, aj keď samotná funkcia nie je daná.
Používa sa pri zmene mierky obrazu.
Používa sa pri modelovaní AI.
Používa sa na výučbu NLP atď.

Čítaj viac,

Interpolačný vzorec
Vzorec lineárnej interpolácie

Príklady Použitie Lagrangeovho interpolačného vzorca

Pozrime sa na niekoľko vzorových otázok o vzorci Lagrangeovej interpolácie.

Príklad 1: Nájdite hodnotu y v x = 2 pre danú množinu bodov (1, 2), (3, 4)

Riešenie:

Vzhľadom na to,

(X₀, a₀) = (1, 2)
(X₁, a₁) = (3, 4)
Lagrangeov interpolačný vzorec prvého rádu je,

$y~=~frac{(x-x_1)}{(x_0-x_1)}krát y_0+frac{(x-x_0)}{(x_1-x_0)}krát y_1$

Pri x = 2

a $=~frac{(2-3)}{(1-3)}krát 2+frac{(2-1)}{(3-1)}krát 4$

y = (-2/-2) + (4/2)

y = 1 + 2 = 3

Hodnota y v x = 2 je 3

Príklad 2: Nájdite hodnotu y v x = 5 pre danú množinu bodov (9, 2), (3, 10)

Riešenie:

Vzhľadom na to,

(X₀, a₀) = (9, 2)
(X₁, a₁) = (3, 10)
Lagrangeov interpolačný vzorec prvého rádu je,

$y~=~frac{(x-x_1)}{(x_0-x_1)}krát y_0+frac{(x-x_0)}{(x_1-x_0)}krát y_1$

Pri x = 5

$y~=~frac{(5-3)}{(9-3)}krát 2+frac{(5-9)}{(3-9)}krát 10$

y = (4/6) + (-40/-6)

y = (2/3) + (20/3)

y = 22/3 = 7,33

Hodnota y pri x = 5 je 7,33

Príklad 3: Nájdite hodnotu y v x = 1 pre danú množinu bodov (1, 6), (3, 4), (2, 5)

Riešenie:

Vzhľadom na to,
je špeciálna postava

(X₀, a₀) = (1, 6)
(X₁, a₁) = (3, 4)
(X₂, a₂) = (2, 5)
Lagrangeov interpolačný vzorec druhého rádu je,

$y~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}krát y_0+frac{(x-x_0)(x-x_2)}{(x_1 -x_0)(x_1-x_2)}krát y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}krát y_2$

Pri x = 1

$y~=~frac{(1-3)(1-2)}{(1-3)(1-2)}krát 6+frac{(1-1)(1-2)}{( 3-1)(3-2)}krát 4+frac{(1-1)(1-3)}{(2-1)(2-3)}krát 5 y~=~ frac{(-2)(-1)}{(-2)(-1)}krát 6+frac{(0)(-1)}{(2)(1)}krát 4+frac {(0)(-2)}{(1)(-1)}krát 5$

y = (12/2) + 0 + 0

y = 6

Hodnota y pri x = 1 je 6

Príklad 4: Nájdite hodnotu y v x = 10 pre danú množinu bodov (9, 6), (3, 5), (1, 12)

Riešenie:

Vzhľadom na to,

(X₀, a₀) = (9, 6)
(X₁, a₁) = (3, 5)
(X₂, a₂) = (1, 12)
Lagrangeov interpolačný vzorec druhého rádu je,

$y~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}krát y_0+frac{(x-x_0)(x-x_2)}{(x_1 -x_0)(x_1-x_2)}krát y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}krát y_2$

Pri x = 10

$y~=~frac{(10-3)(10-1)}{(9-3)(9-1)}krát 6+frac{(10-9)(10-1)}{( 3-9)(3-1)}krát 5+frac{(10-9)(10-3)}{(1-9)(1-3)}krát 12 y~=~ frac{(7)(9)}{(6)(8)}krát 6+frac{(1)(9)}{(-6)(2)}krát 5+frac{(1) (7)}{(-8)(-2)}krát 12$
čítať z csv java

y = (63/8) + (-15/4) + (21/4)

y = (63-30 + 42)/8

y = 75/8 = 9,375

Hodnota y pri x = 10 je 9,375

Príklad 5: Nájdite hodnotu y v x = 7 pre danú množinu bodov (1, 10), (2, 4), (3, 4), (5, 7)

Riešenie:

Vzhľadom na to,

(X₀, a₀) = (1, 10)
(X₁, a₁) = (2, 4)
(X₂, a₂) = (3, 4)
(X₃, a₃) = (5, 7)
Lagrangeov interpolačný vzorec tretieho rádu je,

$y~=~frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)}krát y_0+frac{(x-x_0) )(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)}krát y_1+frac{(x-x_0)(x-x_1)(x-x_3) }{(x_2-x_0)(x_2-x_1)(x_2-x_3)}krát y_2+frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1 )(x_3-x_2)}krát y_3$

Pri x = 7

$y~=~frac{(7-2)(7-3)(7-5)}{(1-2)(1-3)(1-5)}krát 10+frac{(7- 1)(7-3)(7-5)}{(2-1)(2-3)(2-5)}krát 4+frac{(7-1)(7-2)(7- 5)}{(3-1)(3-2)(3-5)}krát 4+frac{(7-1)(7-2)(7-3)}{(5-1)( 5-2)(5-3)}krát 7 y~=~frac{(5)(4)(2)}{(-1)(-2)(-4)}krát 10+ frac{(6)(4)(2)}{(1)(-1)(-3)}krát 4+frac{(6)(5)(2)}{(2)(1) (-2)}krát 4+frac{(6)(5)(4)}{(4)(3)(2)}krát 7$

y = -50 + 64 – 60 + 35

y = 99 – 110 = - jedenásť

Hodnota y v x = 7 je -11

Príklad 6: Nájdite hodnotu y v x = 10 pre danú množinu bodov (5, 12), (6, 13), (7, 14), (8, 15)

Riešenie:

Vzhľadom na to,

(X₀, a₀) = (5, 12)
(X₁, a₁) = (6, 13)
(X₂, a₂) = (7, 14)
(X₃, a₃) = (8, 15)
Lagrangeov interpolačný vzorec tretieho rádu je,
java ahoj svetový príklad

$y~=~frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)}krát y_0+frac{(x-x_0) )(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)}krát y_1+frac{(x-x_0)(x-x_1)(x-x_3) }{(x_2-x_0)(x_2-x_1)(x_2-x_3)}krát y_2+frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1 )(x_3-x_2)}krát y_3$

Pri x = 10,

$y~=~frac{(10-6)(10-7)(10-8)}{(5-6)(5-7)(5-8)}krát 12+frac{(10- 5)(10-7)(10-8)}{(6-5)(6-7)(6-8)}krát 13+frac{(10-5)(10-6)(10- 8)}{(7-5)(7-6)(7-8)}krát 14+frac{(10-5)(10-6)(10-7)}{(8-5)( 8-6)(8-7)}krát 15 y~=~frac{(4)(3)(2)}{(-1)(-2)(-3)}krát 12+ frac{(5)(3)(2)}{(1)(-1)(-2)}krát 13+frac{(5)(4)(2)}{(2)(1) (-1)}krát 14+frac{(5)(4)(3)}{(3)(2)(1)}krát 15$

y = -48 + 195 – 280 + 150

y = 17

Hodnota y pri x = 10 je 17

Príklad 7: Nájdite hodnotu y v x = 0 pre danú množinu bodov (-2, 5), (1, 7)

Riešenie:

Vzhľadom na to,

(X₀, a₀) = (-2, 5)
(X₁, a₁) = (1, 7)
Lagrangeov interpolačný vzorec prvého rádu je,

$y~=~frac{(x-x_1)}{(x_0-x_1)}krát y_0+frac{(x-x_0)}{(x_1-x_0)}krát y_1$

Pri x = 0,

$y~=~frac{(0-1)}{(-2-1)}krát 5+frac{(0+2)}{(1+2)}krát 7$

y = (5/3) + (14/3)

y = 19/3 = 6,33

Hodnota y pri x = 0 je 6,33

Časté otázky o Lagrangeovom interpolačnom vzorci

1. Čo je Lagrangeov interpolačný vzorec?

Lagrangeov vzorec interpolácie je vzorec, ktorý sa používa na nájdenie hodnoty závislej premennej funkcie pre ľubovoľnú nezávislú premennú, aj keď samotná funkcia nie je daná.

2. Aké sú aplikácie Lagrangeovho interpolačného vzorca?

Lagrangesov vzorec má rôzne aplikácie v modernej matematike a dátových vedách,

Používa sa na AI model Traning.
Používa sa pri spracovaní obrazu.
Používa sa pri grafovaní 3-D a vyšších kriviek atď.

3. Čo je Lagrangeov interpolačný vzorec prvého rádu?

Lagrangesov interpolačný vzorec prvého rádu je,

f(x) = (x – x ₁ )/(X ₀ - X ₁ )×f ₀ + (x – x ₀ )/(X ₁ - X ₀ )×f ₁

4. Čo je Lagrangeov interpolačný vzorec druhého rádu?

Lagrangesov interpolačný vzorec druhého rádu je,

f(x) = [(x – x ₁ ) (x – x ₂ )/(X ₀ - X ₁ )(X ₀ - X ₂ )] × f ₀ + [(x – x ₀ ) (x – x ₂ )/(X ₁ - X ₀ )(X ₁ - X ₂ )] × f ₁ + [(x – x ₀ ) (x – x ₁ )/(X ₂ - X ₀ )(X ₂ - X ₂ )] × f ₀