Je každý obdĺžnik kosoštvorec? Obdĺžnik je dvojrozmerný geometrický útvar znázornený štyrmi stranami a štyrmi rohmi. Obdĺžnik obsahuje strany také, že dĺžka protiľahlých strán je rovnaká a tieto strany sú navzájom rovnobežné. Strany zdieľajú roh zo susedných strán s uhlom 90° medzi nimi. Preto sú v obdĺžniku štyri pravé uhly.

Obsah
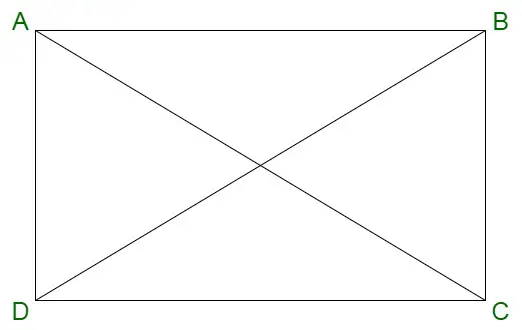
Obdĺžnik
Vlastnosti obdĺžnika sú uvedené nižšie:
- Má štyri hrany a štyri rohy, známe ako vrcholy.
- Uhlopriečky obdĺžnika sa navzájom pretínajú.
- Plocha obdĺžnika je ekvivalentná súčinu jeho dĺžky a šírky.
- Každý vrchol má uhol rovný 90O
- Protiľahlé strany obdĺžnika sú rovnaké a navzájom rovnobežné.
- Obvod sa rovná dvojnásobku súčtu jeho dĺžky a šírky.
- Súčet všetkých vnútorných uhlov sa rovná 360 stupňom
Obvod obdĺžnika
Celkové posunutie, ktoré prejde cez hranicu obdĺžnika, možno nazvať ako obvod. Keďže dĺžka aj šírka sú označené jednotkovou dĺžkou, obvod sa meria aj v jednotke dĺžky.
Obvod môže byť označený,
Obvod, P = 2 (dĺžka + šírka)
Oblasť obdĺžnika
Oblasť pokrytá dvojrozmerným geometrickým útvarom v rovine sa nazýva plocha útvaru. Plocha obdĺžnika je teda plocha zahrnutá do jeho hraníc. Meria sa v štvorcových jednotkách. Plocha je ekvivalentná súčinu dĺžky a šírky obdĺžnika.
Oblasť možno označiť,
Plocha, A = dĺžka × šírka jednotky štvorcových
Uhlopriečka obdĺžnikového vzorca
Diagonály akéhokoľvek geometrického útvaru spájajú alternatívne vrcholy. Dĺžku uhlopriečok obdĺžnika možno vypočítať podľa nasledujúceho vzorca označeného ako d,
d = sqrt{( l^2 + w^2)} kde,
l = dĺžka obdĺžnika
w = šírka obdĺžnika
Prečítajte si podrobne: Vlastnosti obdĺžnika: definícia, vzorce, príklady
Rhombus
Kosoštvorec je tiež známy ako štvorstranný štvoruholník. Považuje sa za špeciálny prípad rovnobežníka. Kosoštvorec obsahuje rovnobežné protiľahlé strany a rovnaké protiľahlé uhly. Kosoštvorec je známy aj pod názvom diamant alebo kosoštvorcový diamant. Kosoštvorec obsahuje všetky strany kosoštvorca rovnako dlhé. Taktiež uhlopriečky kosoštvorca sa navzájom pretínajú v pravom uhle.
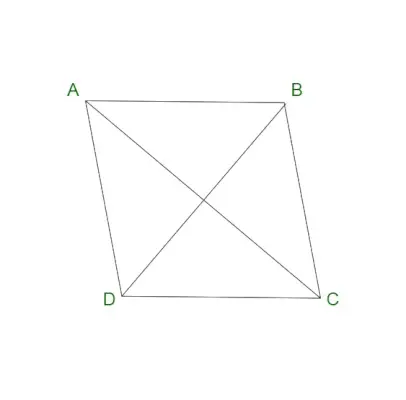
Vlastnosti kosoštvorca
Kosoštvorec má nasledujúce vlastnosti:
- Kosoštvorec obsahuje všetky rovnaké strany.
- Uhlopriečky kosoštvorca sa navzájom pretínajú v pravom uhle.
- Opačné strany kosoštvorca sú svojou povahou rovnobežné.
- Súčet dvoch susedných uhlov kosoštvorca sa rovná 180O.
- V rámci kosoštvorca nie je žiadny popisujúci kruh.
- Okolo kosoštvorca neexistuje opísaný kruh.
- Diagonály kosoštvorca vedú k vytvoreniu štyroch pravouhlých trojuholníkov.
- Tieto trojuholníky sú navzájom zhodné.
- Opačné uhly kosoštvorca sú rovnaké.
- Keď spojíte stred strán kosoštvorca, vytvorí sa obdĺžnik.
- Keď sa spoja stredy polovice uhlopriečky, vytvorí sa ďalší kosoštvorec.
Obvod kosoštvorca
Obvod kosoštvorca je definovaný ako celková dĺžka jeho hraníc tvoriacich obrazec. Môže sa tiež označiť ako celkový súčet dĺžky štyroch strán kosoštvorca. Obvod kosoštvorca je definovaný:
Obvod, P = 4a jednotiek
kde uhlopriečky kosoštvorca sú označené d1& d2a „a“ je strana.
Oblasť Rhombus
Oblasť kosoštvorca je definovaná ako oblasť uzavretá v dvojrozmernej rovine. Plocha kosoštvorca je ekvivalentná súčinu uhlopriečok kosoštvorca delených 2. Plochu kosoštvorca možno definovať podľa tohto vzorca:
Plocha, A =
frac{(d_1 imes d_2)}{2} štvorcových jednotiekkde d1a d2sú uhlopriečky kosoštvorca.
Ľahko si môžeme všimnúť, že každý kosoštvorec je rovnobežník, ale naopak to neplatí. Štvorec možno považovať za špeciálny prípad kosoštvorca, pretože obsahuje štyri strany rovnakej dĺžky. Štvorec má všetky pravé uhly. Všetky uhly kosoštvorca však nemusia byť nevyhnutne pravé . Napokon, kosoštvorec obsahujúci pravé uhly možno považovať za štvorec. Preto môžeme povedať,
- Všetky kosoštvorce sú rovnobežníky.
- Všetky rovnobežníky nie sú kosoštvorce.
- Všetky kosoštvorce nie sú štvorce.
- Všetky štvorce sú kosoštvorce.
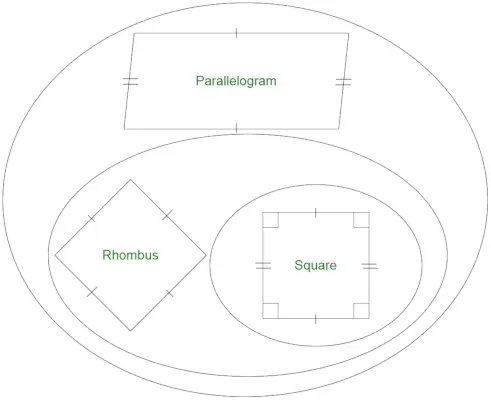
Je každý obdĺžnik kosoštvorec?
Obdĺžnik je geometrický útvar, ktorý nemá všetky rovnaké strany. Štvorec je špeciálny prípad obdĺžnika so všetkými rovnakými stranami. Pretože vieme, že kosoštvorec má všetky rovnaké strany. Množiny obdĺžnikov a kosoštvorcov sa pretínajú iba v prípade štvorcov. Obdĺžnik teda nie je kosoštvorec.
apurva padgaonkar

Prečo je kosoštvorec obdĺžnik?
Kosoštvorec je špeciálny prípad obdĺžnika. Pretože vieme, že uhlopriečky kosoštvorca sa pretínajú v rovnakých uhloch, zatiaľ čo uhlopriečky obdĺžnika majú rovnakú dĺžku. Po spojení stredových bodov strán kosoštvorca sa vytvorí obdĺžnik.
Čítajte viac: Prečo kosoštvorec nie je štvorec?
Vzorové otázky – Je každý obdĺžnik kosoštvorec?
Otázka 1. Vypočítajte plochu obdĺžnikového rámu, ktorý má 6 palcov dĺžka a šírka 3 cm.
Riešenie:
Keďže vieme,
Plocha obdĺžnika = (dĺžka × šírka) štvorcové jednotky.
Nahradením hodnôt dostaneme,
plocha obdĺžnikového rámu = 6 × 3 = 18 štvorcových palcov
Otázka 2. Nájdite dĺžku uhlopriečky obdĺžnika, ktorý má dĺžku 12 cm a šírku 8 cm.
Riešenie:
Vieme,
Diagonálna dĺžka,
D =
sqrt{ L^2+W^2} ⇒ D =
sqrt{12^2+8^2} ⇒ D =
sqrt{144 + 64} ⇒ D = √208
⇒ D = 4√3
Otázka 3. Nájdite plochu kosoštvorca s dvomi dĺžkami uhlopriečky d 1 a d 2 byť 6 cm a 12 cm.
Riešenie:
Máme,
Uhlopriečka d1= 6 cm
Uhlopriečka d2= 12 cm
Plocha kosoštvorca je daná,
A =
frac{(d_1 imes d_2)}{2} štvorcových jednotiekA =
frac{( 6 imes 12)}{2} A =
frac{72}{2} A = 36 cm2
Preto plocha kosoštvorca = 36 cm2.
Otázka 4. Rozdiel medzi kosoštvorcom a obdĺžnikom?
Riešenie:
| Nehnuteľnosť | Rhombus | Obdĺžnik |
| Strany | Rovnaké strany. | Opačné strany sú si rovné. |
| Uhlopriečky | Uhlopriečky sa navzájom pretínajú v uhle 90°. Uhlopriečky zvierajú v strede pravý uhol. | Diagonály sa navzájom pretínajú v rôznych uhloch. Jeden uhol je tupý a druhý je ostrý. Uhlopriečky zvierajú v strede rôzne uhly – tupý uhol a ostrý uhol. |
| Uhly | Opačné uhly sú rovnaké. Susedné uhly sčítajú až 180°. | Opačné a susedné uhly sú rovnaké. Uhol, ktorý zvierajú susedné strany obdĺžnika, je 90°. |
