Obmedzenia tradičných binárnych vyhľadávacích stromov môžu byť frustrujúce. Zoznámte sa s B-Stromom, multitalentovanou dátovou štruktúrou, ktorá dokáže ľahko spracovať obrovské množstvo dát. Pokiaľ ide o ukladanie a vyhľadávanie veľkého množstva údajov, tradičné binárne vyhľadávacie stromy sa môžu stať nepraktickými z dôvodu ich slabého výkonu a vysokej spotreby pamäte. B-stromy, tiež známe ako B-strom alebo Balanced Tree, sú typom samovyvažujúceho stromu, ktorý bol špeciálne navrhnutý na prekonanie týchto obmedzení.
Na rozdiel od tradičných binárnych vyhľadávacích stromov sa B-stromy vyznačujú veľkým počtom kľúčov, ktoré môžu uložiť do jedného uzla, a preto sú známe aj ako veľké stromy kľúčov. Každý uzol v B-strome môže obsahovať viacero kľúčov, čo umožňuje stromu mať väčší faktor vetvenia, a teda menšiu výšku. Táto plytká výška vedie k menšiemu počtu vstupov a výstupov disku, čo má za následok rýchlejšie operácie vyhľadávania a vkladania. B-Stromy sú obzvlášť vhodné pre úložné systémy, ktoré majú pomalý a objemný prístup k údajom, ako sú pevné disky, flash pamäť a CD-ROM.
B-Trees udržiava rovnováhu tým, že zabezpečuje, aby mal každý uzol minimálny počet kľúčov, takže strom je vždy vyvážený. Táto rovnováha zaručuje, že časová zložitosť operácií ako vkladanie, mazanie a vyhľadávanie je vždy O(log n), bez ohľadu na počiatočný tvar stromu.
Časová zložitosť B-stromu:
| pán č. | Algoritmus | Časová zložitosť |
|---|---|---|
| 1. | Vyhľadávanie | O (log n) |
| 2. | Vložiť | O (log n) |
| 3. | Odstrániť | O (log n) |
Poznámka: n je celkový počet prvkov v B-strome
koľko váži kat timpf
Vlastnosti B-stromu:
- Všetky listy sú na rovnakej úrovni.
- B-Strom je definovaný pojmom minimálny stupeň „ t ‘. Hodnota „ t “ závisí od veľkosti bloku disku.
- Každý uzol okrem koreňa musí obsahovať aspoň t-1 kľúčov. Koreň môže obsahovať minimálne 1 kľúč.
- Všetky uzly (vrátane koreňového) môžu obsahovať najviac ( 2*t – 1 ) kľúče.
- Počet potomkov uzla sa rovná počtu kľúčov v ňom plus 1 .
- Všetky kľúče uzla sú zoradené v rastúcom poradí. Dieťa medzi dvoma kľúčmi k1 a k2 obsahuje všetky klávesy v rozsahu od k1 a k2 .
- B-Strom rastie a zmenšuje sa z koreňa, ktorý je na rozdiel od Binary Search Tree. Stromy binárneho vyhľadávania rastú smerom nadol a tiež sa smerom nadol zmenšujú.
- Rovnako ako ostatné vyvážené binárne vyhľadávacie stromy, časová zložitosť vyhľadávania, vkladania a odstraňovania je O(log n).
- Vloženie uzla do B-stromu sa deje iba v listovom uzle.
Nasleduje príklad B-stromu minimálneho poriadku 5
Poznámka: že v praktických B-stromoch je hodnota minimálnej objednávky oveľa vyššia ako 5.

Vo vyššie uvedenom diagrame môžeme vidieť, že všetky listové uzly sú na rovnakej úrovni a všetky nelistové nemajú žiadny prázdny podstrom a majú kľúče o jeden menší ako počet ich potomkov.
Zaujímavé fakty o B-stromoch:
- Minimálna výška B-stromu, ktorá môže existovať s n počtom uzlov a m je maximálny počet potomkov, ktoré môže mať uzol, je:
- Maximálna výška B-stromu, ktorá môže existovať s n počtom uzlov a t je minimálny počet potomkov, ktoré môže mať nekoreňový uzol, je:
a
Prechod v B-strome:
Traversal je tiež podobný ako Inorder traversal Binary Tree. Začneme od dieťaťa najviac vľavo, rekurzívne vytlačíme dieťa najviac vľavo a potom zopakujeme rovnaký postup pre zostávajúce deti a kľúče. Nakoniec rekurzívne vytlačte dieťa úplne vpravo.
Operácia vyhľadávania v B-strome:
Vyhľadávanie je podobné ako vyhľadávanie v strome binárneho vyhľadávania. Nech kľúč, ktorý sa má hľadať, je k.
- Začnite od koreňa a rekurzívne prejdite nadol.
- Pre každý navštívený nelistový uzol,
- Ak má uzol kľúč, jednoducho uzol vrátime.
- V opačnom prípade sa vrátime nadol k príslušnému potomkovi (Dieťa, ktoré je tesne pred prvým väčším kľúčom) uzla.
- Ak dosiahneme listový uzol a nenájdeme k v listovom uzle, vrátime hodnotu NULL.
Vyhľadávanie v B-strome je podobné ako v binárnom strome. Algoritmus je podobný a ide s rekurziou. Na každej úrovni je vyhľadávanie optimalizované tak, že ak hodnota kľúča nie je prítomná v rozsahu nadradenej položky, potom je kľúč prítomný v inej vetve. Keďže tieto hodnoty obmedzujú vyhľadávanie, sú známe aj ako limitné hodnoty alebo separačné hodnoty. Ak dosiahneme listový uzol a nenájdeme požadovaný kľúč, zobrazí sa NULL.
Algoritmus na vyhľadávanie prvku v B-strome:-
C++
struct> Node {> >int> n;> >int> key[MAX_KEYS];> >Node* child[MAX_CHILDREN];> >bool> leaf;> };> Node* BtreeSearch(Node* x,>int> k) {> >int> i = 0;> >while> (i n && k>x->key[i]) {> >i++;> >}> >if> (i n && k == x->kľúč[i]) {> >return> x;> >}> >if> (x->list) {> >return> nullptr;> >}> >return> BtreeSearch(x->dieťa[i], k);> }> |
>
>
C
BtreeSearch(x, k)> >i = 1> > >// n[x] means number of keys in x node> >while> i ? n[x] and k ? keyi[x]> >do> i = i + 1> >if> i n[x] and k = keyi[x]> >then>return> (x, i)> >if> leaf [x]> >then>return> NIL> >else> >return> BtreeSearch(ci[x], k)> |
>
>
Java
class> Node {> >int> n;> >int>[] key =>new> int>[MAX_KEYS];> >Node[] child =>new> Node[MAX_CHILDREN];> >boolean> leaf;> }> Node BtreeSearch(Node x,>int> k) {> >int> i =>0>;> >while> (i = x.key[i]) {> >i++;> >}> >if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }> |
>
>
Python3
class> Node:> >def> __init__(>self>):> >self>.n>=> 0> >self>.key>=> [>0>]>*> MAX_KEYS> >self>.child>=> [>None>]>*> MAX_CHILDREN> >self>.leaf>=> True> def> BtreeSearch(x, k):> >i>=> 0> >while> i and k>= x.key[i]: i += 1 if i a k == x.key[i]: return x if x.leaf: return None return BtreeSearch(x.child[i], k)> |
>
>
C#
class> Node {> >public> int> n;> >public> int>[] key =>new> int>[MAX_KEYS];> >public> Node[] child =>new> Node[MAX_CHILDREN];> >public> bool> leaf;> }> Node BtreeSearch(Node x,>int> k) {> >int> i = 0;> >while> (i = x.key[i]) {> >i++;> >}> >if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }> |
>
>
Javascript
// Define a Node class with properties n, key, child, and leaf> class Node {> >constructor() {> >this>.n = 0;> >this>.key =>new> Array(MAX_KEYS);> >this>.child =>new> Array(MAX_CHILDREN);> >this>.leaf =>false>;> >}> }> // Define a function BtreeSearch that takes in a Node object x and an integer k> function> BtreeSearch(x, k) {> >let i = 0;> >while> (i = x.key[i]) {> >i++;> >}> >if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }> |
>
>
Príklady:
Neena Gupta
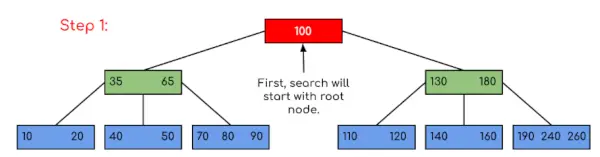
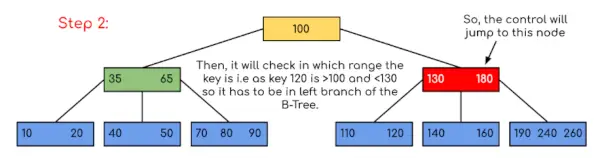
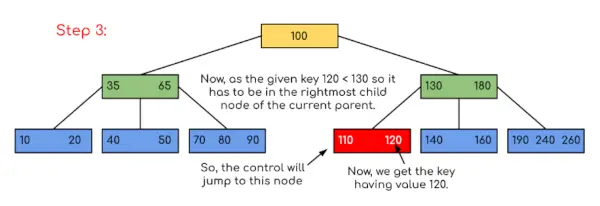
Vstup: Vyhľadajte 120 v danom B-strome.
Riešenie:
koľko miest je v Spojených štátoch
V tomto príklade môžeme vidieť, že naše vyhľadávanie bolo zredukované len obmedzením šancí, kde by sa mohol nachádzať kľúč obsahujúci hodnotu. Podobne, ak vo vyššie uvedenom príklade máme hľadať 180, potom sa ovládanie zastaví v kroku 2, pretože program zistí, že kľúč 180 je prítomný v aktuálnom uzle. A podobne, ak sa má vyhľadať 90, potom ako 90 <100, takže to automaticky prejde do ľavého podstromu, a preto tok riadenia bude prebiehať podobne, ako je znázornené vo vyššie uvedenom príklade.
Nižšie je uvedená implementácia vyššie uvedeného prístupu:
C++
// C++ implementation of search() and traverse() methods> #include> using> namespace> std;> // A BTree node> class> BTreeNode {> >int>* keys;>// An array of keys> >int> t;>// Minimum degree (defines the range for number> >// of keys)> >BTreeNode** C;>// An array of child pointers> >int> n;>// Current number of keys> >bool> leaf;>// Is true when node is leaf. Otherwise false> public>:> >BTreeNode(>int> _t,>bool> _leaf);>// Constructor> >// A function to traverse all nodes in a subtree rooted> >// with this node> >void> traverse();> >// A function to search a key in the subtree rooted with> >// this node.> >BTreeNode*> >search(>int> k);>// returns NULL if k is not present.> >// Make the BTree friend of this so that we can access> >// private members of this class in BTree functions> >friend> class> BTree;> };> // A BTree> class> BTree {> >BTreeNode* root;>// Pointer to root node> >int> t;>// Minimum degree> public>:> >// Constructor (Initializes tree as empty)> >BTree(>int> _t)> >{> >root = NULL;> >t = _t;> >}> >// function to traverse the tree> >void> traverse()> >{> >if> (root != NULL)> >root->traverse();> >}> >// function to search a key in this tree> >BTreeNode* search(>int> k)> >{> >return> (root == NULL) ? NULL : root->search(k);> >}> };> // Constructor for BTreeNode class> BTreeNode::BTreeNode(>int> _t,>bool> _leaf)> {> >// Copy the given minimum degree and leaf property> >t = _t;> >leaf = _leaf;> >// Allocate memory for maximum number of possible keys> >// and child pointers> >keys =>new> int>[2 * t - 1];> >C =>new> BTreeNode*[2 * t];> >// Initialize the number of keys as 0> >n = 0;> }> // Function to traverse all nodes in a subtree rooted with> // this node> void> BTreeNode::traverse()> {> >// There are n keys and n+1 children, traverse through n> >// keys and first n children> >int> i;> >for> (i = 0; i // If this is not leaf, then before printing key[i], // traverse the subtree rooted with child C[i]. if (leaf == false) C[i]->prechádzať (); cout<< ' ' << keys[i]; } // Print the subtree rooted with last child if (leaf == false) C[i]->prechádzať (); } // Funkcia na vyhľadávanie kľúča k v podstrome zakorenenom týmto uzlom BTreeNode* BTreeNode::search(int k) { // Nájdenie prvého kľúča väčšieho alebo rovného k int i = 0; while (i kľúče[i]) i++; // Ak sa nájdený kľúč rovná k, vráti tento uzol if (keys[i] == k) return this; // Ak sa tu kľúč nenájde a toto je listový uzol if (list == true) return NULL; // Prejsť na príslušné dieťa return C[i]->search(k); }> |
>
>
Java
// Java program to illustrate the sum of two numbers> // A BTree> class> Btree {> >public> BTreeNode root;>// Pointer to root node> >public> int> t;>// Minimum degree> >// Constructor (Initializes tree as empty)> >Btree(>int> t)> >{> >this>.root =>null>;> >this>.t = t;> >}> >// function to traverse the tree> >public> void> traverse()> >{> >if> (>this>.root !=>null>)> >this>.root.traverse();> >System.out.println();> >}> >// function to search a key in this tree> >public> BTreeNode search(>int> k)> >{> >if> (>this>.root ==>null>)> >return> null>;> >else> >return> this>.root.search(k);> >}> }> // A BTree node> class> BTreeNode {> >int>[] keys;>// An array of keys> >int> t;>// Minimum degree (defines the range for number> >// of keys)> >BTreeNode[] C;>// An array of child pointers> >int> n;>// Current number of keys> >boolean> >leaf;>// Is true when node is leaf. Otherwise false> >// Constructor> >BTreeNode(>int> t,>boolean> leaf)> >{> >this>.t = t;> >this>.leaf = leaf;> >this>.keys =>new> int>[>2> * t ->1>];> >this>.C =>new> BTreeNode[>2> * t];> >this>.n =>0>;> >}> >// A function to traverse all nodes in a subtree rooted> >// with this node> >public> void> traverse()> >{> >// There are n keys and n+1 children, traverse> >// through n keys and first n children> >int> i =>0>;> >for> (i =>0>; i <>this>.n; i++) {> >// If this is not leaf, then before printing> >// key[i], traverse the subtree rooted with> >// child C[i].> >if> (>this>.leaf ==>false>) {> >C[i].traverse();> >}> >System.out.print(keys[i] +>' '>);> >}> >// Print the subtree rooted with last child> >if> (leaf ==>false>)> >C[i].traverse();> >}> >// A function to search a key in the subtree rooted with> >// this node.> >BTreeNode search(>int> k)> >{>// returns NULL if k is not present.> >// Find the first key greater than or equal to k> >int> i =>0>;> >while> (i keys[i])> >i++;> >// If the found key is equal to k, return this node> >if> (keys[i] == k)> >return> this>;> >// If the key is not found here and this is a leaf> >// node> >if> (leaf ==>true>)> >return> null>;> >// Go to the appropriate child> >return> C[i].search(k);> >}> }> |
>
>
Python3
# Create a node> class> BTreeNode:> >def> __init__(>self>, leaf>=>False>):> >self>.leaf>=> leaf> >self>.keys>=> []> >self>.child>=> []> # Tree> class> BTree:> >def> __init__(>self>, t):> >self>.root>=> BTreeNode(>True>)> >self>.t>=> t> ># Insert node> >def> insert(>self>, k):> >root>=> self>.root> >if> len>(root.keys)>=>=> (>2> *> self>.t)>-> 1>:> >temp>=> BTreeNode()> >self>.root>=> temp> >temp.child.insert(>0>, root)> >self>.split_child(temp,>0>)> >self>.insert_non_full(temp, k)> >else>:> >self>.insert_non_full(root, k)> ># Insert nonfull> >def> insert_non_full(>self>, x, k):> >i>=> len>(x.keys)>-> 1> >if> x.leaf:> >x.keys.append((>None>,>None>))> >while> i>>=> 0> and> k[>0>] 0]: x.keys[i + 1] = x.keys[i] i -= 1 x.keys[i + 1] = k else: while i>= 0 a k[0] 0]: i -= 1 i += 1 if len(x.child[i].keys) == (2 * self.t) - 1: self.split_child(x, i) if k[0]> x.keys[i][0]: i += 1 self.insert_non_full(x.child[i], k) # Rozdeliť dieťa def split_child(self, x, i): t = self .t y = x.child[i] z = BTreeNode(y.list) x.child.insert(i + 1, z) x.keys.insert(i, y.keys[t - 1]) z.keys = y.keys[t: (2 * t) - 1] y.keys = y.keys[0: t - 1] ak nie y.list: z.child = y.child[t: 2 * t] r. dieťa = y.child[0: t - 1] # Tlač stromu def print_tree(self, x, l=0): print('Úroveň ', l, ' ', len(x.keys), end=':') for i in x.keys: print(i, end=' ') print() l += 1 if len(x.child)> 0: for i in x.child: self.print_tree(i, l) # Kľúč vyhľadávania v strome def search_key(self, k, x=None): ak x nie je None: i = 0, zatiaľ čo i |
>
>
C#
// C# program to illustrate the sum of two numbers> using> System;> // A BTree> class> Btree {> >public> BTreeNode root;>// Pointer to root node> >public> int> t;>// Minimum degree> >// Constructor (Initializes tree as empty)> >Btree(>int> t)> >{> >this>.root =>null>;> >this>.t = t;> >}> >// function to traverse the tree> >public> void> traverse()> >{> >if> (>this>.root !=>null>)> >this>.root.traverse();> >Console.WriteLine();> >}> >// function to search a key in this tree> >public> BTreeNode search(>int> k)> >{> >if> (>this>.root ==>null>)> >return> null>;> >else> >return> this>.root.search(k);> >}> }> // A BTree node> class> BTreeNode {> >int>[] keys;>// An array of keys> >int> t;>// Minimum degree (defines the range for number> >// of keys)> >BTreeNode[] C;>// An array of child pointers> >int> n;>// Current number of keys> >bool> leaf;>// Is true when node is leaf. Otherwise false> >// Constructor> >BTreeNode(>int> t,>bool> leaf)> >{> >this>.t = t;> >this>.leaf = leaf;> >this>.keys =>new> int>[2 * t - 1];> >this>.C =>new> BTreeNode[2 * t];> >this>.n = 0;> >}> >// A function to traverse all nodes in a subtree rooted> >// with this node> >public> void> traverse()> >{> >// There are n keys and n+1 children, traverse> >// through n keys and first n children> >int> i = 0;> >for> (i = 0; i <>this>.n; i++) {> >// If this is not leaf, then before printing> >// key[i], traverse the subtree rooted with> >// child C[i].> >if> (>this>.leaf ==>false>) {> >C[i].traverse();> >}> >Console.Write(keys[i] +>' '>);> >}> >// Print the subtree rooted with last child> >if> (leaf ==>false>)> >C[i].traverse();> >}> >// A function to search a key in the subtree rooted with> >// this node.> >public> BTreeNode search(>int> k)> >{>// returns NULL if k is not present.> >// Find the first key greater than or equal to k> >int> i = 0;> >while> (i keys[i])> >i++;> >// If the found key is equal to k, return this node> >if> (keys[i] == k)> >return> this>;> >// If the key is not found here and this is a leaf> >// node> >if> (leaf ==>true>)> >return> null>;> >// Go to the appropriate child> >return> C[i].search(k);> >}> }> // This code is contributed by Rajput-Ji> |
>
>
Javascript
// Javascript program to illustrate the sum of two numbers> // A BTree> class Btree> {> >// Constructor (Initializes tree as empty)> >constructor(t)> >{> >this>.root =>null>;> >this>.t = t;> >}> > >// function to traverse the tree> >traverse()> >{> >if> (>this>.root !=>null>)> >this>.root.traverse();> >document.write(>' '>);> >}> > >// function to search a key in this tree> >search(k)> >{> >if> (>this>.root ==>null>)> >return> null>;> >else> >return> this>.root.search(k);> >}> > }> // A BTree node> class BTreeNode> {> >// Constructor> >constructor(t,leaf)> >{> >this>.t = t;> >this>.leaf = leaf;> >this>.keys =>new> Array(2 * t - 1);> >this>.C =>new> Array(2 * t);> >this>.n = 0;> >}> >// A function to traverse all nodes in a subtree rooted with this node> >traverse()> >{> >// There are n keys and n+1 children, traverse through n keys> >// and first n children> >let i = 0;> >for> (i = 0; i <>this>.n; i++) {> > >// If this is not leaf, then before printing key[i],> >// traverse the subtree rooted with child C[i].> >if> (>this>.leaf ==>false>) {> >C[i].traverse();> >}> >document.write(keys[i] +>' '>);> >}> > >// Print the subtree rooted with last child> >if> (leaf ==>false>)> >C[i].traverse();> >}> > >// A function to search a key in the subtree rooted with this node.> >search(k)>// returns NULL if k is not present.> >{> > >// Find the first key greater than or equal to k> >let i = 0;> >while> (i keys[i])> >i++;> > >// If the found key is equal to k, return this node> >if> (keys[i] == k)> >return> this>;> > >// If the key is not found here and this is a leaf node> >if> (leaf ==>true>)> >return> null>;> > >// Go to the appropriate child> >return> C[i].search(k);> >}> }> // This code is contributed by patel2127> |
>
>
Poznámka: Vyššie uvedený kód neobsahuje program ovládača. Kompletný program prinesieme v ďalšom príspevku Vloženie B-stromu .
Existujú dve konvencie na definovanie B-stromu, jedna je definovať podľa minimálneho stupňa, druhá je definovať podľa poradia. Dodržiavali sme konvenciu minimálneho stupňa a budeme sa ňou riadiť aj v nasledujúcich príspevkoch na B-strome. Názvy premenných použité vo vyššie uvedenom programe sa tiež ponechajú rovnaké
java inicializovať pole
Aplikácia B-stromov:
- Používa sa vo veľkých databázach na prístup k údajom uloženým na disku
- Vyhľadávanie údajov v súbore údajov je možné dosiahnuť pomocou B-Stromu za výrazne kratší čas
- Pomocou funkcie indexovania je možné dosiahnuť viacúrovňové indexovanie.
- Väčšina serverov tiež používa prístup B-stromu.
- B-stromy sa používajú v CAD systémoch na organizáciu a vyhľadávanie geometrických údajov.
- B-stromy sa používajú aj v iných oblastiach, ako je spracovanie prirodzeného jazyka, počítačové siete a kryptografia.
Výhody B-stromov:
- B-stromy majú garantovanú časovú zložitosť O(log n) pre základné operácie ako vkladanie, mazanie a vyhľadávanie, vďaka čomu sú vhodné pre veľké súbory údajov a aplikácie v reálnom čase.
- B-stromy sú samovyvažujúce.
- Vysoká súbežnosť a vysoká priepustnosť.
- Efektívne využitie úložiska.
Nevýhody B-stromov:
- B-stromy sú založené na dátových štruktúrach na disku a môžu mať vysoké využitie disku.
- Nie je to najlepšie pre všetky prípady.
- Pomalé v porovnaní s inými dátovými štruktúrami.
Vkladanie a mazanie:
Vloženie B-stromu
Vymazanie B-stromu