Chamtivá metóda je jednou zo stratégií ako Rozdeľ a panuj, ktorá sa používa na riešenie problémov. Táto metóda sa používa na riešenie optimalizačných problémov. Optimalizačný problém je problém, ktorý vyžaduje maximálne alebo minimálne výsledky. Poďme pochopiť cez niektoré pojmy.
Greedyho metóda je najjednoduchší a priamočiary prístup. Nie je to algoritmus, ale technika. Hlavnou funkciou tohto prístupu je, že rozhodnutie sa prijíma na základe aktuálne dostupných informácií. Bez ohľadu na to, aké sú aktuálne informácie, rozhodnutie sa urobí bez obáv o vplyv súčasného rozhodnutia v budúcnosti.
operačný systém linux
Táto technika sa v podstate používa na určenie realizovateľného riešenia, ktoré môže alebo nemusí byť optimálne. Realizovateľným riešením je podmnožina, ktorá spĺňa dané kritériá. Optimálne riešenie je riešenie, ktoré je najlepším a najpriaznivejším riešením v podskupine. V prípade realizovateľných, ak viac ako jedno riešenie spĺňa dané kritériá, potom sa tieto riešenia budú považovať za realizovateľné, pričom optimálne riešenie je najlepšie riešenie spomedzi všetkých riešení.
Charakteristika Greedyho metódy
Nasledovné sú charakteristiky chamtivé metódy:
- Na zostavenie riešenia optimálnym spôsobom tento algoritmus vytvorí dve sady, kde jedna sada obsahuje všetky vybrané položky a druhá sada obsahuje odmietnuté položky.
- Chamtivý algoritmus robí dobré miestne voľby v nádeji, že riešenie by malo byť realizovateľné alebo optimálne.
Komponenty Greedy Algorithmu
Komponenty, ktoré možno použiť v chamtivom algoritme, sú:
stredové tlačidlo css
Aplikácie Greedy Algorithm
- Používa sa pri hľadaní najkratšej cesty.
- Používa sa na nájdenie minimálneho kostry pomocou primovho algoritmu alebo Kruskalovho algoritmu.
- Používa sa v postupnosti úloh s termínom.
- Tento algoritmus sa tiež používa na riešenie problému s frakčným batohom.
Pseudo kód Greedy Algorithm
Algorithm Greedy (a, n) { Solution : = 0; for i = 0 to n do { x: = select(a); if feasible(solution, x) { Solution: = union(solution , x) } return solution; } } Vyššie uvedené je chamtivý algoritmus. Na začiatku je riešeniu priradená nulová hodnota. Odovzdáme pole a počet prvkov v chamtivom algoritme. Vo vnútri cyklu for vyberáme prvok jeden po druhom a kontrolujeme, či je riešenie realizovateľné alebo nie. Ak je riešenie realizovateľné, vykonáme spojenie.
Poďme to pochopiť na príklade.
Predpokladajme, že existuje problém „P“. Chcem cestovať z bodu A do bodu B, ako je uvedené nižšie:
P: A → B
Problém je v tom, že túto cestu musíme absolvovať z A do B. Existujú rôzne riešenia, ako ísť z A do B. Z A do B môžeme ísť chôdza, auto, bicykel, vlak, lietadlo , atď. V ceste je obmedzenie, že túto cestu musíme prejsť do 12 hodín. Len ak pôjdem vlakom alebo lietadlom, túto vzdialenosť prejdem do 12 hodín. Existuje mnoho riešení tohto problému, ale existujú iba dve riešenia, ktoré spĺňajú obmedzenie.
Ak povieme, že cestu musíme pokryť s minimálnymi nákladmi. To znamená, že túto vzdialenosť musíme prejsť čo najmenšiu, takže tento problém je známy ako problém minimalizácie. Doteraz máme dve realizovateľné riešenia, t. j. jedno vlakom a druhé letecky. Keďže cestovanie vlakom povedie k minimálnym nákladom, je to optimálne riešenie. Optimálne riešenie je tiež realizovateľné riešenie, ale poskytujúce najlepší výsledok, takže riešenie je optimálnym riešením s minimálnymi nákladmi. Bolo by len jedno optimálne riešenie.
Problém, ktorý vyžaduje buď minimálny alebo maximálny výsledok, je potom známy ako problém optimalizácie. Chamtivá metóda je jednou zo stratégií používaných na riešenie optimalizačných problémov.
ako vrátiť pole v jave
Nevýhody použitia Greedyho algoritmu
Chamtivý algoritmus robí rozhodnutia na základe informácií dostupných v každej fáze bez zohľadnenia širšieho problému. Takže môže existovať možnosť, že chamtivé riešenie neposkytuje najlepšie riešenie pre každý problém.
Nasleduje výber lokálneho optima v každej fáze so zámerom nájsť globálne optimum. Poďme to pochopiť na príklade.
Zvážte graf, ktorý je uvedený nižšie:
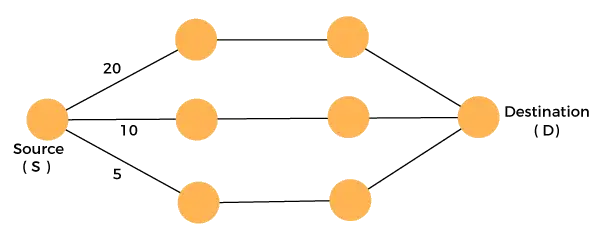
Musíme cestovať od zdroja do cieľa s minimálnymi nákladmi. Keďže máme tri realizovateľné riešenia s cenovými cestami ako 10, 20 a 5. 5 je cesta minimálnych nákladov, takže je to optimálne riešenie. Toto je lokálne optimum a týmto spôsobom nájdeme lokálne optimum v každej fáze, aby sme vypočítali globálne optimálne riešenie.
pole reťazcov v programovaní v c
