Výška paralelného vzorca slúži na výpočet výšky rovnobežníka. Výška rovnobežníka je kolmá vzdialenosť medzi základnou stranou a protiľahlou rovnobežnou stranou. Rovnobežník možno definovať ako štvoruholník, v ktorom sú protiľahlé strany rovnobežné a dĺžka týchto protiľahlých strán je tiež rovnaká.

Výška vzorca paralelogramu

Opačné uhly rovnobežníka sú tiež rovnaké. Zistite viac o výške vzorca rovnobežníka s odvodením podrobne nižšie.

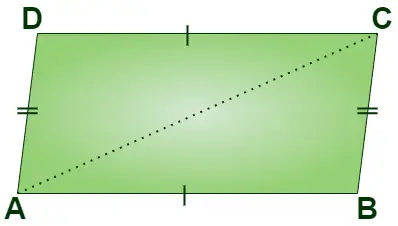
Výška vzorca paralelogramu

Výška vzorca paralelogramu

Výška rovnobežníka sa vypočíta pomocou vzorca Plocha sa rovná základni vynásobenej výškou, takže ak plocha Paralelogram je známe, že jeho výška sa vypočíta vydelením plochy jej základňou.

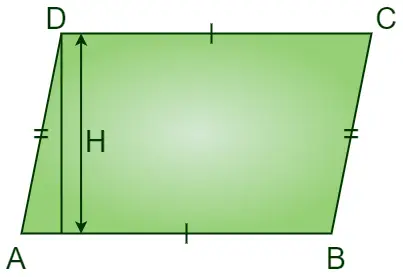
Výška vzorca Parallelogram je odvodená od vzorca oblasti, oblasť paralelogramu možno nájsť pomocou základnej dĺžky a výšky rovnobežníka.

Plocha = základňa × výška

Výška = plocha/základňa

Obvod rovnobežníka

Obvod je definovaný ako súčet všetkých strán, pomocou ktorých je zostrojený uzavretý obrazec. V prípade rovnobežníka má 4 strany, z ktorých sú protiľahlé strany rovnaké, takže obvod je súčtom všetkých štyroch strán.

Zoberme si teda mieru opačných strán ako X a Y

Obvod rovnobežníka = X + Y + X + Y = 2X + 2Y = 2 (X + Y)

Obvod = 2 (X + Y)

Súvisiace zdroje

• Paralelné čiary
• Oblasť obdĺžnika
• Obvod obdĺžnika

Vyriešený príklad výšky rovnobežníka

Príklad 1: Nájdite výšku rovnobežníka, ak jeho plocha je 625 cm ² a dĺžka základne je 25 cm.

Riešenie:

Výšku rovnobežníka možno vypočítať pomocou vzorca výšky rovnobežníka

Výška = plocha / základňa

Výška = 625/25

Výška = 25 cm.

Výška rovnobežníka je teda 25 cm

Príklad 2: Nájdite plochu rovnobežníka, ktorého základňa je 20 cm a výška je 15 cm.

Riešenie:

Plocha rovnobežníka = základňa × výška

Základňa a výška sú uvedené ako 20 cm a 15 cm.

Plocha = 20 × 15

Plocha = 300 cm.

Príklad 3: Obvod rovnobežníka je 226 cm a jedna strana rovnobežníka má dĺžku 12 cm, nájdite mieru druhej strany.

Riešenie:

architektúra úľa

Obvod rovnobežníka = 2 (X + Y)

Kde X je dĺžka jednej strany a Y dĺžka druhej strany, nech X = 12 cm

226 = 2 (X + Y)

2(X + Y) = 226

2(12 + Y) = 226

24 + 2 Y = 226

2Y = 226 – 24

2Y = 202

Y = 202/2

Y = 101 cm.

Príklad 4: Nájdite výšku rovnobežníka, ak jeho plocha je 800 cm ² a dĺžka základne je 40 cm.

Riešenie

Výšku rovnobežníka možno vypočítať pomocou vzorca výšky rovnobežníka

Výška = plocha / základňa

Výška = 800/40

Výška = 20 cm.

Výška rovnobežníka je teda 20 cm

Príklad 5: Obvod rovnobežníka je 400 cm a jedna strana rovnobežníka má dĺžku 80 cm, nájdite mieru druhej strany.

Riešenie:

Obvod rovnobežníka = 2 (X + Y)

Kde X je dĺžka jednej strany a Y dĺžka druhej strany, nech X = 80 cm

400 = 2 (X + Y)

2(X + Y) = 400

2(80 + Y) = 400

160 + 2Y = 400

2Y = 400 – 160

2Y = 240

Y = 120 cm.

Výška vzorca paralelogramu

Aký je vzorec pre výšku rovnobežníka?

Vzorec pre výšku rovnobežníka je plocha(a)/základňa(b).

Aká je základňa a výška rovnobežníka?

Základňa označuje dĺžku strany a Výška je dĺžka kolmice medzi dvoma rovnobežnými čiarami.

Aká je výška rovnobežníka?

java inicializovať pole

Výška rovnobežníka sa označuje ako kolmá vzdialenosť medzi dvoma rovnobežnými čiarami rovnobežníka.

Aká je oblasť rovnobežníka?

Oblasť rovnobežníka sa označuje ako priestor vo vnútri hranice rovnobežníka.