Zoradenie vloženia a zoradenie výberu sú dva populárne triediace algoritmy a ich hlavný rozdiel spočíva v tom, ako vyberajú a umiestňujú prvky do zoradeného poradia.
Zoradenie výberu:
- Pri triedení výberu je vstupné pole rozdelené na dve časti: triedenú časť a netriedenú časť.
- Algoritmus opakovane nájde minimálny prvok v netriedenej časti a vymení ho za prvok úplne vľavo v nezoradenej časti, čím rozšíri zoradenú časť o jeden prvok.
- Triedenie výberu má vo všetkých prípadoch časovú zložitosť O(n^2).
Zoradenie vloženia:
- Pri triedení vložením je vstupné pole tiež rozdelené na dve časti: triedenú časť a netriedenú časť.
Algoritmus vyberie prvok z nevytriedenej časti a umiestni ho na správnu pozíciu v zoradenej časti, pričom väčšie prvky posunie o jednu pozíciu doprava.
Zoradenie vložením má v najhoršom prípade časovú zložitosť O(n^2), ale môže fungovať lepšie na čiastočne zoradených poliach, pričom časová zložitosť v najlepšom prípade je O(n).
Hlavné rozdiely: - Triedenie výberu skenuje nezoradenú časť, aby našiel minimálny prvok, zatiaľ čo triedenie vložením skenuje zoradenú časť, aby našiel správnu pozíciu na umiestnenie prvku.
Výberové zoradenie vyžaduje menej swapov ako vloženie, ale viac porovnaní.
Vloženie triedenia je efektívnejšie ako triedenie výberu, keď je vstupné pole čiastočne alebo takmer zoradené, zatiaľ čo triedenie výberu funguje lepšie, keď je pole veľmi nezoradené.
Stručne povedané, oba algoritmy majú podobnú časovú zložitosť, ale ich výber a spôsoby umiestnenia sa líšia. Výber medzi nimi závisí od charakteristík vstupných údajov a špecifických požiadaviek daného problému.
Výhody triedenia vkladania:
- Jednoduché a ľahko pochopiteľné a implementovateľné.
- Efektívne pre malé súbory údajov alebo takmer zoradené údaje.
- Algoritmus triedenia na mieste, čo znamená, že nevyžaduje dodatočnú pamäť.
- Stabilný algoritmus triedenia, čo znamená, že zachováva relatívne poradie rovnakých prvkov vo vstupnom poli.
Nevýhody triedenia vkladania:
- Neefektívne pre veľké súbory údajov alebo údaje v opačnom poradí, pričom časová zložitosť v najhoršom prípade je O(n^2).
- Zoradenie vkladania má veľa swapov, čo môže na moderných počítačoch spomaliť.
Výhody triedenia výberu:
- Jednoduché a ľahko pochopiteľné a implementovateľné.
- Efektívne pre malé súbory údajov alebo takmer zoradené údaje.
- Algoritmus triedenia na mieste, čo znamená, že nevyžaduje dodatočnú pamäť.
Nevýhody výberu druhu:
- Neefektívne pre veľké súbory údajov, s najhorším prípadom časovej zložitosti O(n^2).
- Výberové triedenie má veľa porovnaní, čo môže na moderných počítačoch spomaliť.
- Nestabilný algoritmus triedenia, čo znamená, že nemusí zachovať relatívne poradie rovnakých prvkov vo vstupnom poli.
V tomto článku budeme diskutovať o rozdieloch medzi triedením vloženia a triedením výberu:
Zoradenie vloženia je jednoduchý triediaci algoritmus, ktorý funguje podobne ako triedenie hracích kariet v rukách. Pole je virtuálne rozdelené na triedenú a netriedenú časť. Hodnoty z nevytriedenej časti sa vyberú a umiestnia na správnu pozíciu v triedenej časti.
Algoritmus:
Ak chcete zoradiť pole veľkosti n vzostupne:
- Iterujte z arr[1] do arr[n] cez pole.
- Porovnajte aktuálny prvok (kľúč) s jeho predchodcom.
- Ak je kľúčový prvok menší ako jeho predchodca, porovnajte ho s predchádzajúcimi prvkami. Posuňte väčšie prvky o jednu pozíciu nahor, aby ste vytvorili priestor pre vymenený prvok.
Nižšie je uvedený obrázok na ilustráciu zoradenia vloženia:
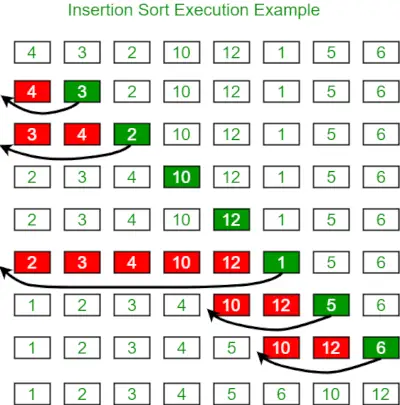
Nižšie je uvedený program pre to isté:
C++
// C++ program for the insertion sort> #include> using> namespace> std;> // Function to sort an array using> // insertion sort> void> insertionSort(>int> arr[],>int> n)> {> >int> i, key, j;> >for> (i = 1; i key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> kľúč) { arr[j + 1] = arr[j]; j = j-1; } arr[j + 1] = kľúč; } } // Funkcia na tlač poľa veľkosti N void printArray(int arr[], int n) { int i; // Vytlačí pole pre (i = 0; i cout<< arr[i] << ' '; } cout << endl; } // Driver Code int main() { int arr[] = { 12, 11, 13, 5, 6 }; int N = sizeof(arr) / sizeof(arr[0]); // Function Call insertionSort(arr, N); printArray(arr, N); return 0; }> |
>
>
Java
// Java program for the above approach> import> java.util.*;> class> GFG> {> > // Function to sort an array using> // insertion sort> static> void> insertionSort(>int> arr[],>int> n)> {> >int> i, key, j;> >for> (i =>1>; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> kľúč) { arr[j + 1] = arr[j]; j = j-1; } arr[j + 1] = kľúč; } } // Funkcia na tlač poľa veľkosti N static void printArray(int arr[], int n) { int i; // Vytlačí pole pre (i = 0; i System.out.print(arr[i] + ' '); } System.out.println(); } // Kód ovládača public static void main(String[ ] args) { int arr[] = { 12, 11, 13, 5, 6 } int N = arr.length // Volanie funkcie insertionSort(arr, N } } //); K tomuto kódu prispel code_hunt |
>
# Python 3 program for the insertion sort># Function to sort an array using># insertion sort>def>insertionSort(arr, n):>>i>=>0>>key>=>0>>j>=>0>>for>i>in>range>(>1>,n,>1>):>>key>=>arr[i]>>j>=>i>->1>># Move elements of arr[0..i-1],>># that are greater than key to>># one position ahead of their>># current position>>while>(j>>=>0>and>arr[j]>kľúč):>>arr[j>+>1>]>=>arr[j]>>j>=>j>->1>>arr[j>+>1>]>=>key># Function to print an array of size N>def>printArray(arr, n):>>i>=>0>># Print the array>>for>i>in>range>(n):>>print>(arr[i],end>=>' '>)>>print>(>' '>,end>=>'')># Driver Code>if>__name__>=>=>'__main__'>:>>arr>=>[>12>,>11>,>13>,>5>,>6>]>>N>=>len>(arr)>># Function Call>>insertionSort(arr, N)>>printArray(arr, N)>>># This code is contributed by bgangwar59.>>>C#
// C# program for the above approach>using>System;>class>GFG>{>>// Function to sort an array using>>// insertion sort>>static>void>insertionSort(>int>[] arr,>int>n)>>{>>int>i, key, j;>>for>(i = 1; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> kľúč) { arr[j + 1] = arr[j]; j = j-1; } arr[j + 1] = kľúč; } } // Funkcia na tlač poľa veľkosti N static void printArray(int[] arr, int n) { int i; // Vytlačí pole pre (i = 0; i { Console.Write(arr[i] + ' '); } Console.WriteLine(); } // kód ovládača static public void Main() { int[] arr = new int[] { 12, 11, 13, 5, 6 }; int N = arr.Dlzka; prispel Dharanendra L V>>>Javascript
>// JavaScript program for the above approach>// Function to sort an array using>// insertion sort>function>insertionSort(arr,n)>{>>let i, key, j;>>for>(i = 1; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> kľúč) { arr[j + 1] = arr[j]; j = j-1; } arr[j + 1] = kľúč; } } // Funkcia na tlač poľa veľkosti N function printArray(arr,n) { nech i; // Vytlačí pole pre (i = 0; i document.write(arr[i] + ' '); } document.write(' '); } // Kód ovládača nech arr=[12, 11 , 13, 5, 6] nech N = arr.length // Volanie funkcie insertionSort(arr, N) // Tento kód prispel avanitrachhadiya2155;>5 6 11 12 13> The triedenie výberu Algoritmus triedi pole opakovaným nájdením minimálneho prvku (vzhľadom na vzostupné poradie) z nezoradenej časti a jeho umiestnením na začiatok. Algoritmus udržiava dve podpole v danom poli.
- Podpole je už zoradené.
- Zostávajúce podpole nie je zoradené.
V každej iterácii triedenia výberu sa vyberie minimálny prvok (vzhľadom na vzostupné poradie) z nezoradeného podpola a presunie sa do zoradeného podpola.
Nižšie je uvedený príklad, ktorý vysvetľuje vyššie uvedené kroky:
arr[] = 64 25 12 22 11 // Find the minimum element in arr[0...4] // and place it at beginning 11 25 12 22 64 // Find the minimum element in arr[1...4] // and place it at beginning of arr[1...4] 11 12 25 22 64 // Find the minimum element in arr[2...4] // and place it at beginning of arr[2...4] 11 12 22 25 64 // Find the minimum element in arr[3...4] // and place it at beginning of arr[3...4] 11 12 22 25 64>Nižšie je uvedený program pre to isté:
C++
// C++ program for implementation of>// selection sort>#include>using>namespace>std;>// Function to swap two number>void>swap(>int>* xp,>int>* yp)>{>>int>temp = *xp;>>*xp = *yp;>>*yp = temp;>}>// Function to implement the selection>// sort>void>selectionSort(>int>arr[],>int>n)>{>>int>i, j, min_idx;>>// One by one move boundary of>>// unsorted subarray>>for>(i = 0; i // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element swap(&arr[min_idx], &arr[i]); } } // Function to print an array void printArray(int arr[], int size) { int i; for (i = 0; i cout << arr[i] << ' '; } cout << endl; } // Driver Code int main() { int arr[] = { 64, 25, 12, 22, 11 }; int n = sizeof(arr) / sizeof(arr[0]); // Function Call selectionSort(arr, n); cout << 'Sorted array: '; // Print the array printArray(arr, n); return 0; }>>>Java
// Java program for implementation of>// selection sort>import>java.util.*;>class>GFG>{>// Function to implement the selection>// sort>static>void>selectionSort(>int>arr[],>int>n)>{>>int>i, j, min_idx;>>// One by one move boundary of>>// unsorted subarray>>for>(i =>0>; i 1; i++) { // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element int temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array static void printArray(int arr[], int size) { int i; for (i = 0; i System.out.print(arr[i]+ ' '); } System.out.println(); } // Driver Code public static void main(String[] args) { int arr[] = { 64, 25, 12, 22, 11 }; int n = arr.length; // Function Call selectionSort(arr, n); System.out.print('Sorted array: '); // Print the array printArray(arr, n); } } // This code is contributed by aashish1995>>>Python3
# Python3 program for implementation of># selection sort># Function to implement the selection># sort>def>selectionSort(arr, n):>># One by one move boundary of>># unsorted subarray>>for>i>in>range>(n>->1>):>># Find the minimum element>># in unsorted array>>min_idx>=>i>>for>j>in>range>(i>+>1>, n):>>if>(arr[j] min_idx = j # Swap the found minimum element # with the first element arr[min_idx], arr[i] = arr[i], arr[min_idx] # Function to print an array def printArray(arr, size): for i in range(size): print(arr[i], end = ' ') print() # Driver Code if __name__ == '__main__': arr = [64, 25, 12, 22, 11] n = len(arr) # Function Call selectionSort(arr, n) print('Sorted array: ') # Print the array printArray(arr, n) # This code is contributed by ukasp>>>C#
čo je špeciálny znak
// C# program for implementation of>// selection sort>using>System;>public>class>GFG>{>// Function to implement the selection>// sort>static>void>selectionSort(>int>[]arr,>int>n)>{>>int>i, j, min_idx;>>// One by one move boundary of>>// unsorted subarray>>for>(i = 0; i { // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element int temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array static void printArray(int []arr, int size) { int i; for (i = 0; i Console.Write(arr[i]+ ' '); } Console.WriteLine(); } // Driver Code public static void Main(String[] args) { int []arr = { 64, 25, 12, 22, 11 }; int n = arr.Length; // Function Call selectionSort(arr, n); Console.Write('Sorted array: '); // Print the array printArray(arr, n); } } // This code is contributed by gauravrajput1>>>Javascript
>// Javascript program for implementation of>// selection sort>// Function to implement the selection>// sort>function>selectionSort(arr, n)>{>>let i, j, min_idx;>>>// One by one move boundary of>>// unsorted subarray>>for>(i = 0; i { // Find the minimum element // in unsorted array min_idx = i; for(j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element let temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array function printArray(arr, size) { let i; for(i = 0; i { document.write(arr[i] + ' '); } document.write(' '); } // Driver Code let arr = [ 64, 25, 12, 22, 11 ]; let n = arr.length; // Function Call selectionSort(arr, n); document.write('Sorted array: '); // Print the array printArray(arr, n); // This code is contributed by rag2127>>>Výkon:Sorted array: 11 12 22 25 64>Tabuľkový rozdiel medzi triedením vloženia a triedením výberu:
Triedenie vloženia Výber Zoradiť 1. Vloží hodnotu do vopred zoradeného poľa, aby sa zoradila množina hodnôt v poli. Vyhľadá minimálny / maximálny počet zo zoznamu a zoradí ho vzostupne / zostupne. 2. Je to stabilný triediaci algoritmus. Je to nestabilný triediaci algoritmus. 3. Časová zložitosť v najlepšom prípade je Ω(N), keď je pole už vo vzostupnom poradí. Má Θ(N2) v najhoršom prípade a priemernom prípade. V najlepšom prípade má najhorší prípad a priemerné triedenie výberu zložitosť Θ(N2). 4. Počet porovnávacích operácií vykonaných v tomto triediacom algoritme je menší ako vykonaný swap. Počet porovnávacích operácií vykonaných v tomto triediacom algoritme je väčší ako vykonaný swap. 5. Je to efektívnejšie ako trieda Selection. Je menej efektívny ako typ vkladania. 6. Tu je prvok vopred známy a hľadáme správnu polohu na jeho umiestnenie. Miesto, kam umiestniť prvok, je už známe, hľadáme prvok, ktorý sa má vložiť na túto pozíciu. 7. Zoradenie vloženia sa používa, keď:
- Pole má malý počet prvkov
- Zostáva zoradiť už len niekoľko prvkov
Triedenie výberu sa používa, keď
- Je potrebné triediť malý zoznam
- Na cene výmeny nezáleží
- Kontrola všetkých prvkov je povinná
- Náklady na zápis do pamäte sú dôležité ako vo flash pamäti (počet swapov je O(n) v porovnaní s O(n2) bublinového typu)
8. Triedenie vkladania je adaptívne, t.j. efektívne pre súbory údajov, ktoré sú už v podstate zoradené: časová zložitosť je O(kn) keď každý prvok na vstupe nie je väčší ako k miesta mimo svojej zoradenej polohy Výberové triedenie je miestny porovnávací triediaci algoritmus
