Odstránenie uzla zo stromu AVL je podobné ako v strome binárneho vyhľadávania. Vymazanie môže narušiť faktor rovnováhy stromu AVL, a preto je potrebné strom znovu vyvážiť, aby sa zachovala hodnota AVL. Na tento účel musíme vykonať rotácie. Dva typy rotácie sú L rotácia a R rotácia. Tu budeme diskutovať o rotáciách R. L rotácie sú ich zrkadlovým obrazom.

Ak sa uzol, ktorý sa má vymazať, nachádza v ľavom podstrome kritického uzla, potom je potrebné použiť rotáciu L, ak sa uzol, ktorý sa má vymazať, nachádza v pravom podstrome kritického uzla. , použije sa rotácia R.

Uvažujme, že A je kritický uzol a B je koreňový uzol jeho ľavého podstromu. Ak sa má vymazať uzol X nachádzajúci sa v pravom podstrome A, môžu nastať tri rôzne situácie:

Rotácia R0 (Uzol B má faktor vyváženia 0)

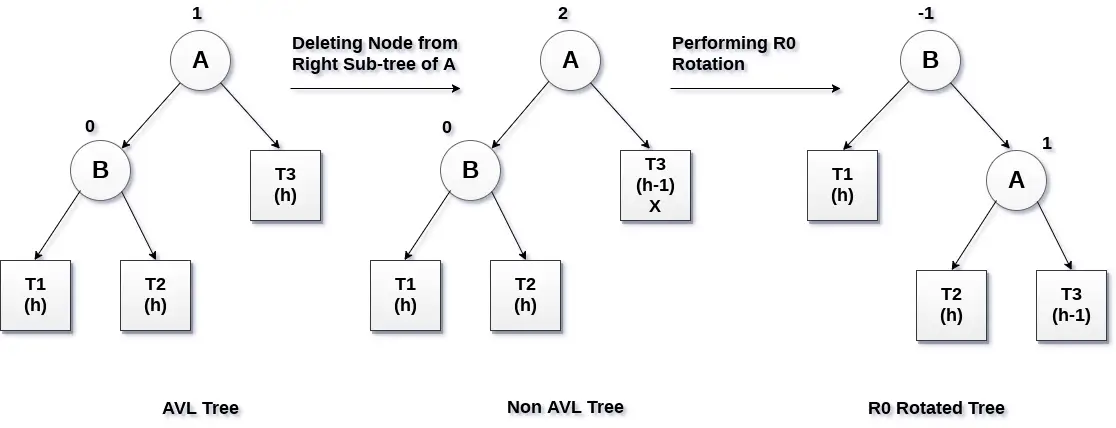
Ak má uzol B nulový faktor rovnováhy a faktor rovnováhy uzla A sa po vymazaní uzla X naruší, strom bude znovu vyvážený rotáciou stromu pomocou rotácie R0.

Kritický uzol A sa presunie doprava a uzol B sa stane koreňom stromu s T1 ako jeho ľavým podstromom. Podstromy T2 a T3 sa stanú ľavým a pravým podstromom uzla A. proces zapojený do rotácie R0 je znázornený na nasledujúcom obrázku.

Príklad:

Odstráňte uzol 30 zo stromu AVL znázorneného na nasledujúcom obrázku.

Riešenie

V tomto prípade má uzol B súčiniteľ rovnováhy 0, preto sa strom otočí pomocou rotácie R0, ako je znázornené na nasledujúcom obrázku. Uzol B(10) sa stane koreňom, zatiaľ čo uzol A sa presunie doprava. Pravý potomok uzla B sa teraz stane ľavým potomkom uzla A.

mapa v jave

Rotácia R1 (Uzol B má faktor vyváženia 1)

Rotácia R1 sa má vykonať, ak je koeficient rovnováhy uzla B 1. Pri rotácii R1 sa kritický uzol A presunie doprava, pričom podstromy T2 a T3 sú jeho ľavým a pravým potomkom. T1 sa má umiestniť ako ľavý podstrom uzla B.

Proces zapojenia do rotácie R1 je znázornený na nasledujúcom obrázku.

Príklad

Odstráňte uzol 55 zo stromu AVL zobrazeného na nasledujúcom obrázku.

Riešenie :

Vymazanie 55 zo stromu AVL naruší faktor rovnováhy uzla 50, t. j. uzla A, ktorý sa stane kritickým uzlom. Toto je podmienka rotácie R1, pri ktorej sa uzol A posunie doprava (zobrazené na obrázku nižšie). Pravá strana B je teraz ľavá od A (t.j. 45).

Proces riešenia je znázornený na nasledujúcom obrázku.

Rotácia R-1 (Uzol B má vyvážený faktor -1)

Rotácia R-1 sa má vykonať, ak má uzol B faktor rovnováhy -1. S týmto prípadom sa zaobchádza rovnako ako s rotáciou LR. V tomto prípade sa uzol C, ktorý je pravým potomkom uzla B, stane koreňovým uzlom stromu s B a A ako jeho ľavým a pravým potomkom.

Podstromy T1, T2 sa stávajú ľavým a pravým podstromom B, zatiaľ čo T3, T4 sa stávajú ľavým a pravým podstromom A.

reťazec v porovnaní s

Proces rotácie R-1 je znázornený na nasledujúcom obrázku.

Príklad

Odstráňte uzol 60 zo stromu AVL znázorneného na nasledujúcom obrázku.

Riešenie:

v tomto prípade má uzol B súčiniteľ rovnováhy -1. Vymazanie uzla 60 naruší vyváženie uzla 50, preto je potrebné ho otočiť o R-1. Uzol C t.j. 45 sa stáva koreňom stromu s uzlom B(40) a A(50) ako jeho ľavým a pravým potomkom.