NFA môže mať nula, jeden alebo viac ako jeden pohyb z daného stavu na danom vstupnom symbole. NFA môže mať aj NULL ťahy (pohyby bez vstupného symbolu). Na druhej strane, DFA má jeden a len jeden pohyb z daného stavu na danom vstupnom symbole.

Kroky na konverziu NFA na DFA:

Krok 1: Preveďte daný NFA na jeho ekvivalentnú tabuľku prechodov
Aby sme previedli NFA na ekvivalentnú tabuľku prechodu, musíme uviesť všetky stavy, vstupné symboly a pravidlá prechodu. Pravidlá prechodu sú znázornené vo forme matice, kde riadky predstavujú aktuálny stav, stĺpce predstavujú vstupný symbol a bunky predstavujú nasledujúci stav.

Krok 2: Vytvorte počiatočný stav DFA
Počiatočný stav DFA je množina všetkých možných počiatočných stavov v NFA. Táto sada sa nazýva epsilon uzáver počiatočného stavu NFA. Uzáver epsilon je množina všetkých stavov, ktoré možno dosiahnuť z počiatočného stavu nasledujúcimi prechodmi epsilon (?).

Krok 3: Vytvorte tabuľku prechodu služby DFA
Prechodová tabuľka DFA je podobná prechodovej tabuľke NFA, ale namiesto jednotlivých stavov predstavujú riadky a stĺpce množiny stavov. Pre každý vstupný symbol obsahuje zodpovedajúca bunka v tabuľke prechodu epsilon uzáver množiny stavov získaných podľa pravidiel prechodu v tabuľke prechodov NFA.

Krok 4: Vytvorte konečné stavy DFA
Konečné stavy DFA sú množiny stavov, ktoré obsahujú aspoň jeden konečný stav z NFA.

Krok 5: Zjednodušte DFA
DFA získaný v predchádzajúcich krokoch môže obsahovať nepotrebné stavy a prechody. Na zjednodušenie DFA môžeme použiť nasledujúce techniky:

• Odstrániť nedostupné stavy: Stavy, ktoré sa nedajú dosiahnuť z počiatočného stavu, môžu byť odstránené zo služby DFA.
• Odstrániť mŕtve stavy: Štáty, ktoré nemôžu viesť ku konečnému stavu, môžu byť odstránené zo služby DFA.
• Zlúčiť ekvivalentné stavy: Štáty, ktoré majú rovnaké pravidlá prechodu pre všetky vstupné symboly, možno zlúčiť do jedného stavu.

Krok 6: Opakujte kroky 3-5, kým už nebude možné ďalšie zjednodušenie
Po zjednodušení DFA opakujeme kroky 3 až 5, až kým nebude možné ďalšie zjednodušenie. Výsledná získaná DFA je minimalizovaný ekvivalent DFA k danej NFA.

porovnateľný reťazec

Príklad: Zvážte nasledujúci NFA znázornený na obrázku 1.

Nasledujú rôzne parametre pre NFA. Q = { q0, q1, q2}? = (a, b) F = { q2}? (Prechodová funkcia NFA)

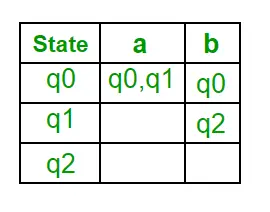
Krok 1: Q' = ? Krok 2: Q' = {q0} Krok 3: Pre každý stav v Q' nájdite stavy pre každý vstupný symbol. V súčasnosti je stav v Q' q0, nájdite pohyby z q0 na vstupnom symbole a a b pomocou prechodovej funkcie NFA a aktualizujte tabuľku prechodov DFA. ?‘ (Prechodová funkcia DFA)

Teraz sa { q0, q1 } bude považovať za jeden stav. Keďže jeho záznam nie je v Q', pridajte ho do Q'. Takže Q' = { q0, { q0, q1 } } Teraz, pohyby zo stavu { q0, q1 } na rôznych vstupných symboloch nie sú prítomné v tabuľke prechodov DFA, vypočítame to takto: ?' ( { q0, q1 } , a) = ? (q0, a) ? ? ( q1, a ) = { q0, q1 } ?‘ ( { q0, q1 }, b ) = ? (q0, b) ? ? ( q1, b ) = { q0, q2 } Teraz aktualizujeme tabuľku prechodov DFA. ?‘ (Prechodová funkcia DFA)

Teraz sa { q0, q2 } bude považovať za jeden stav. Keďže jeho záznam nie je v Q', pridajte ho do Q'. Takže Q' = { q0, { q0, q1 }, { q0, q2 } } Teraz, pohyby zo stavu {q0, q2} na rôznych vstupných symboloch nie sú prítomné v tabuľke prechodov DFA, vypočítame to takto: ?' ( { q0, q2 }, a ) = ? (q0, a) ? ? ( q2, a ) = { q0, q1 } ?‘ ( { q0, q2 }, b ) = ? (q0, b) ? ? ( q2, b ) = { q0 } Teraz aktualizujeme tabuľku prechodu DFA. ?‘ (Prechodová funkcia DFA)

je proteínový tuk

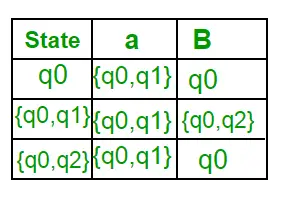
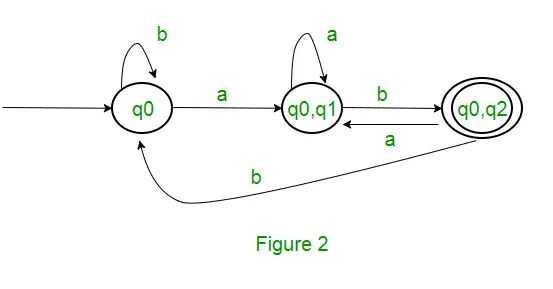
Keďže sa nevygeneruje žiadny nový stav, konverzia je hotová. Konečný stav DFA bude stav, ktorého komponentom je q2, t. j. { q0, q2 } Nasledujú rôzne parametre pre DFA. Q’ = { q0, { q0, q1 }, { q0, q2 } } ? = (a, b) F = { { q0, q2 } } a prechodová funkcia ?‘, ako je uvedené vyššie. Konečná DFA pre vyššie uvedenú NFA je znázornená na obrázku 2.

Poznámka : Niekedy nie je jednoduché previesť regulárny výraz na DFA. Najprv môžete previesť regulárny výraz na NFA a potom NFA na DFA.

otázka: Počet stavov v minimálnom deterministickom konečnom automate zodpovedajúcich regulárnemu výrazu (0 + 1)* (10) je ____________.

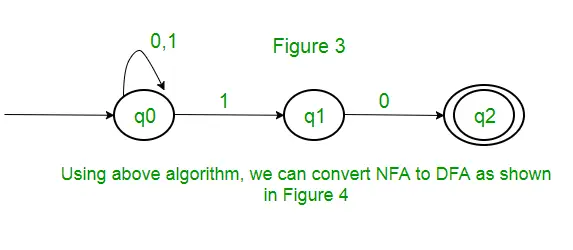
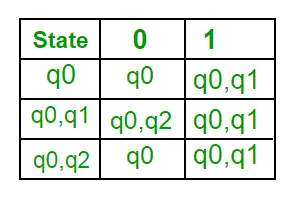
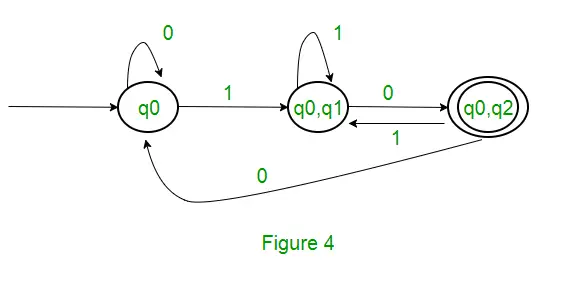
Riešenie : Najprv vytvoríme NFA pre vyššie uvedený výraz. Na vytvorenie NFA pre (0 + 1)* bude NFA v rovnakom stave q0 na vstupnom symbole 0 alebo 1. Potom na zreťazenie pridáme dva ťahy (q0 až q1 pre 1 a q1 až q2 pre 0), ako je znázornené na obrázku 3.

K tomuto článku prispel Sonal Tuteja.