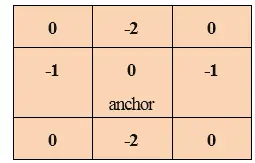
Konvolúcia sa používa na mnoho vecí, ako je výpočet derivácií, detekcia hrán, aplikácia rozmazania atď. a to všetko sa robí pomocou „konvolučného jadra“. Konvolučné jadro je veľmi malá matica a v tejto matici má každá bunka číslo a tiež kotviaci bod.
Kotviaci bod sa používa na zistenie polohy jadra vzhľadom na obrázok. Začína v ľavom hornom rohu obrázka a pohybuje sa postupne po každom pixeli. Jadro prekrýva niekoľko pixelov na každej pozícii na obrázku. Každý pixel, ktorý sa prekrýva, sa vynásobí a potom pridá. A súčet je nastavený ako hodnota aktuálnej pozície.
Konvolúcia je proces, v ktorom sa každý prvok obrazu pridá k svojim miestnym susedom a potom sa zváži jadrom. Súvisí to s formou matematickej konvolúcie.
Proces Android acore sa stále zastavuje
V konvolúcii matica nevykonáva tradičné násobenie matice, ale je označená *.
Predpokladajme, že existujú dve matice 3x3, jedna je jadro a druhá časť obrazu. Pri konvolúcii sa riadky a stĺpce jadra prevrátia a potom sa vynásobia a potom sa vykoná sčítanie. Prvky, ktoré sú prítomné v strede matice, t.j. v [2,2] obrázku, budú vážené kombináciou matice obrázku a váhy budú dané jadrom. Podobne sa zvážia všetky ostatné prvky matice a potom sa vypočítajú váhy.
Nasleduje pseudokód na popis procesu konvolúcie:
reťazec v java metódach
For each image row in input image: For each pixel in image row: Set accumulator to zero For each kernel row in kernel: For each element in kernel row: If element position corresponding* to pixel position then Multiply element value corresponding*to pixelvalue Add result to accumulator Endif Set output image pixel to accumulator
Konvolúciu možno vypočítať pomocou viacerých cyklov for. Ale používanie cyklov for spôsobuje veľa opakovaných výpočtov a tiež sa zvyšuje veľkosť obrazu a jadra. Pomocou techniky diskrétnej Fourierovej transformácie je možné rýchlo vypočítať konvolúciu. Pri tejto technike sa celá operácia konvolúcie prevedie na jednoduché násobenie.
previesť int na reťazec java
Pri konvolúcii problém nastáva, keď je jadro blízko okraja alebo rohov, pretože jadro je dvojrozmerné.
Na prekonanie týchto problémov je možné urobiť nasledovné:
- Tie možno ignorovať
- V blízkosti okrajov je možné vytvoriť ďalšie pixely.
Ďalšie pixely je možné vytvoriť nasledujúcimi spôsobmi:
- Duplicitný okrajový pixel.
- Odrážajú okraje
- Pixely je možné kopírovať z druhého konca.
