Zložený úrok je úrok, ktorý sa počíta oproti sume pôžičky alebo vkladu, v ktorej sa úrok počíta z istiny, ako aj z predtým získaných úrokov.

Spoločný rozdiel medzi zloženým a jednoduchým úrokom je ten, že v zložené úročenie , úrok sa počíta pre sumu istiny, ako aj pre predtým získaný úrok, zatiaľ čo jednoduchý úrok závisí iba od investovanej istiny.

Obsah

• Čo je zložený úrok?
• Zložený úrokový vzorec
• Ako vypočítať zložený úrok?
• Zložený úrokový vzorec – odvodenie
• Polročný vzorec zloženého úročenia
• Vzorec štvrťročného zloženého úročenia
• Vzorec mesačného zloženého úročenia
• Denný vzorec zloženého úročenia
• Vzorec pre periodické zloženie
• Pravidlo 72
• Zložené úročenie po sebe nasledujúcich rokov
• Vzorec kontinuálneho zloženého úrokovania
• Niektoré ďalšie aplikácie zloženého úročenia
• Rozdiel medzi zloženým úročením a jednoduchým úročením
• Príklady zloženého úročenia
• Zložené úročenie – praktické otázky

Čo je zložený úrok?

Zložený úrok je úrok zo sumy istiny, ako aj úrok získaný zo sumy istiny. Slovo Compound Interest sa skladá z dvoch slov Zložený, čo znamená zložený z dvoch alebo viacerých a Úrok znamená peniaze zarobené za požičanie sumy. Zložený úrok sú teda peniaze zarobené na pôžičkách a pozostávajú z dvoch typov úrokov, ktorými sú:

• Úrok z istiny

• Úrok z úroku získaného zo sumy istiny počas Obdobia

Definícia zloženého úročenia

Zložené úročenie je úrok vypočítaný z istiny a predtým získaný úrok. Označuje sa C.I. Je veľmi užitočný pri investíciách a splácaní úverov. Je tiež známy ako úrok z úrokov.

javascript onload skript

Zložené úročenie je veľmi užitočný v bankovom a finančnom sektore a je užitočný aj v iných sektoroch. Niektoré z jeho použití sú:

• Rast počtu obyvateľov krajiny
• Hodnota investície za určité časové obdobie.
• Na zistenie nafúknutých nákladov a amortizovanej hodnoty akéhokoľvek tovaru.
• Na predpovedanie rastu akejkoľvek inštitúcie alebo krajiny.

Zložený úrok (C.I) = suma – istina

Zložený úrokový vzorec

Zložené úročenie sa vypočíta po výpočte celkovej sumy za určité obdobie na základe úrokovej sadzby a počiatočnej istiny. Pre počiatočnú istinu P, úrokovú sadzbu za rok r, časové obdobie t v rokoch, frekvenciu, koľkokrát sa úrok ročne zloží n, vzorec na výpočet CI je nasledujúci:

CI = P(1 + r/100) ⁿ – P

Vyššie uvedený vzorec na výpočet zloženého úroku je pridaný vo forme obrázka nižšie:

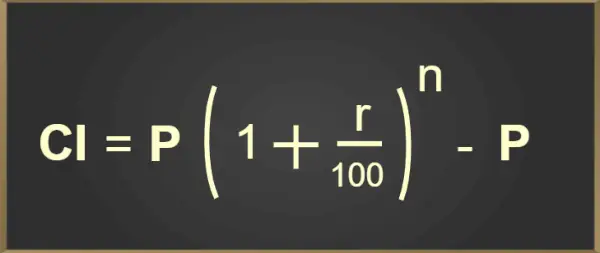
Zložený úrokový vzorec

Kde,

• P = hlavné
• r = úroková sadzba
• n = počet zložených úrokov za rok
• t = čas (v rokoch)

Vzorec pre zložené úročenie môžeme napísať ako:

Zložené úročenie = A – P

Kde,

• A = Celková suma peňazí po zložení
• P = Počiatočná čiastka istiny

Zložený úrok = P(1 + r/n) ^nt -P

Kde,

• P = Počiatočná čiastka istiny
• r = Ročná úroková sadzba
• n = počet zložených úrokov
• t = Počet rokov

Zložený úrok sa môže vypočítať ročne, polročne, štvrťročne, mesačne, denne atď. podľa požiadavky.

Ako vypočítať zložený úrok?

Zložené úročenie je zaplatený úrok z istiny, ako aj naakumulovaný úrok. Úrok získaný v každom intervale sa pripočíta k počiatočnej istine, takže istina sa neustále zvyšuje.

Na nájdenie zloženého úroku použite nasledujúce metódy.

Krok 1: Poznámka, istina, sadzba a uvedené časové obdobie

Krok 2: Vypočítajte množstvo pomocou vzorca A = P(1 + r/100) ⁿ

Krok 3: Nájdite zložený úrok pomocou vzorca CI = suma – istina

V pravidelných intervaloch sa dosiaľ nahromadený úrok spája s existujúcou sumou istiny a následne sa úročí vypočítané pre nového istina . Nová istina sa rovná súčtu počiatočnej istiny a doteraz nahromadených úrokov.

Zložený úrok = úrok z istiny + úrok z úroku istiny (od druhého roku a ďalej)

Zložené úroky sa počítajú v pravidelných intervaloch, ako sú ročné (ročné), polročné, štvrťročné, mesačné, atď; Je to ako, reinvestovanie úrokového výnosu z investície spôsobí, že peniaze časom rastú rýchlejšie! To je presne to, čo zložené úročenie robí s peniazmi. Banky alebo iné finančné organizácie vypočítavajú sumu len na základe zloženého úroku.

Zložený úrokový vzorec – odvodenie

Vzorec zloženého úroku je výkonný nástroj používaný vo financiách na výpočet zarobeného alebo zaplateného úroku z počiatočnej sumy istiny, ktorý zahŕňa počiatočnú istinu aj úrok naakumulovaný za predchádzajúce obdobia. Vzorec pre zložený úrok je daný:

Kde,

• A je budúca hodnota investície alebo úveru vrátane úrokov
• P je istina (počiatočná investícia alebo výška úveru)
• r je ročná úroková sadzba (ako desatinné číslo)
• n je počet zložených úrokov za rok
• to je čas, na ktorý sa peniaze investujú alebo si požičiavajú v rokoch

Jednoduchý úrokový vzorec

Jednoduchý úrok sa počíta len zo sumy istiny. Môže byť vyjadrený vzorcom ,

Zložený úrokový vzorec s kontinuálnym zložením

Keď sa úrok kontinuálne zloží (nekonečne veľakrát za rok), vzorec zloženého úročenia sa odvodí pomocou vzorca kontinuálneho zloženia:

Kde,

• e je Eulerovo číslo (približne 2,71828)
• P je istina
• r je ročná úroková sadzba
• t je čas v rokoch

Vzorec všeobecného zloženého úročenia

Aby sme odvodili všeobecný vzorec zloženého úroku, zvážme zložený úrok n-krát za rok.

Ak P sa zloží n-krát za rok pri ročnej úrokovej sadzbe r, úrok r sa vydelí n a použije sa n-krát za rok. Takže po t rokoch sa vzorec zmení na:

Kde,

• predstavuje úrokovú sadzbu za obdobie zloženia.
• nt je celkový počet období zloženia za t rokov.

Toto vzorec ilustruje, ako počiatočná suma istiny rastie v priebehu času, keď sa úroky zlučujú v pravidelných intervaloch . Keď sa n blíži k nekonečnu (t. j. kontinuálne zlučovanie), vzorec konverguje k kontinuálnemu zloženému vzorcu .

v súhrne zložený úrokový vzorec je výsledkom kontinuálneho zmiešavacieho vzorca prispôsobeného pre jednotlivé obdobia miešania za rok. Umožňuje výpočet budúcej hodnoty investície alebo úveru, pričom sa v pravidelných intervaloch zohľadňuje zložený úrok.

Polročný vzorec zloženého úročenia

Nech je investovaná istina P a úroková sadzba je R % per annum, ktorá sa počíta polročne za „t“ rokov

Ako je zložený polročne, menuje sa istina na konci 6 mesiacov, a dovtedy získaný úrok sa pripočíta k istine a potom sa táto stane novou istinou. Podobne sa vypočíta aj konečná suma.

Vieme,

sadzba = R% per annum zložené polročne

sadzba = (R/2) %

čas je t rokov vieme, že t rokov má 2t pol roka.

teraz

súbor otvorený v jave

A = P (1 + R/200) ^2t

CI = A – P

Vzorec štvrťročného zloženého úročenia

Nech je investovaná istina P a úroková sadzba je R % per annum, ktorá sa zhŕňa štvrťročne za t rokov.

Ako je zložený štvrťročne, istina sa zmení na konci 3 mesiacov, a dovtedy zarobený úrok sa pripočíta k istine a tá sa potom stane novou istinou. Podobne sa vypočíta aj konečná suma.

vieme,

sadzba = R% per annum zložená štvrťročne

sadzba = (R/4) %

čas je t rokov vieme, že t rokov má 4t štvrtí.

teraz

A = P(1 + R/400) ^4t

CI = A – P

Skontrolujte: Štvrťročný vzorec zloženého úročenia

Vzorec mesačného zloženého úročenia

Ak je úrok zložený mesačne, potom počet zložených úrokov bude 12 a úrok každý mesiac bude 1/12 ročného zloženého úroku. Preto je mesačný zložený úrokový vzorec uvedený ako

A = P[1 + (R/1200)] ^12t

CI = A – P

Skontrolujte: Vzorec mesačného zloženého úročenia

Denný vzorec zloženého úročenia

Ak je úrok zložený denne, tak.

Nová úroková sadzba bude R/365 %

n = 365

Preto je vzorec denného zloženého úročenia daný ako,

A = P[1 + (R/36500)] ^{365 t}

CI = A – P

Vzorec pre periodické zloženie

Celková suma vrátane istiny P a zloženého úroku CI je daná vzorcom:

A = P[1 + (r/n)] ^nt

jarná čižma

kde,

• P = hlavné
• A = Konečná suma
• r = Ročná úroková sadzba
• n = počet zložených úrokov
• t = čas (v rokoch)

Zložený úrok je teda:

CI = A – P

Pravidlo 72

Pravidlo 72 je vzorec, ktorý sa používa na odhad, o koľko rokov sa naše peniaze zdvojnásobia, ak sa zrátajú ročne. Pre príklad , ak sú naše peniaze investované na r % zložené ročne, potom to trvá 72/r rokov, kým sa naše peniaze zdvojnásobia.

Tento výpočet je užitočný aj na výpočet nafúknutej hodnoty našich peňazí, t.j. udáva, za koľko rokov sa hodnota nášho majetku zníži na polovicu, ak sa ročne odpíše.

Vzorec pravidla 72

Nasledujúci vzorec sa používa na približný počet rokov, za ktoré sa naša investícia zdvojnásobí.

N = 72/r

kde,

• N je približný počet rokov, za ktoré sa naše peniaze zdvojnásobia
• r je sadzba, pri ktorej sa naše peniaze ročne zložia

Príklad pravidla 72

Predpokladajme, že Kabir investoval 10 00 000 rupií do dlhového fondu, ktorý prináša 8% návratnosť. Zistite, za koľko rokov sa jeho peniaze zdvojnásobia, ak sa zrátajú ročne.

Pomocou vyššie uvedeného vzorca: N = 72/8 = 9 rokov

teda trvá 9 rokov, kým sa Kabirove peniaze zdvojnásobia.

Zložené úročenie po sebe nasledujúcich rokov

Ak máme rovnakú sumu a rovnakú úrokovú sadzbu. C.I. konkrétneho roka je vždy viac ako C.I predchádzajúceho roka. (CI 3. roku je väčší ako CI 2. roku). Rozdiel medzi CI za akékoľvek dva po sebe idúce roky je jeden rok z CI predchádzajúceho roka.

K.I 3. ročníka – K.I 2. ročníka = K.I 2. ročníka × r × 1/100

Rozdiel medzi sumami za ktorékoľvek dva po sebe idúce roky je úrok za jeden rok zo sumy predchádzajúceho roka.

Suma za 3. rok – Suma za 2. rok = Suma za 2. rok × r × 1/100

Kľúčové výsledky

Keď máme rovnakú sumu a rovnakú mieru ,

C.I za n-tý rok = C.I za (n – 1) rok + úrok za jeden rok na C.I za (n – 1) rok

Vzorec kontinuálneho zloženého úrokovania

Vzorec kontinuálneho zlučovania sa vo financiách používa na výpočet konečnej hodnoty investície, ktorá prechádza nepretržitým zlučovaním počas rôznych období a hodnota sa v priebehu času pridáva. Vzorec pre kontinuálne miešanie je uvedený ako

Konečná hodnota = súčasná hodnota × e ^rt

kde,

• r je úroková sadzba
• to je čas

Uč sa viac, Kontinuálny zlučovací vzorec

Niektoré ďalšie aplikácie zloženého úročenia

Rast: Používa sa hlavne na rast, ak sú odvetvia prepojené.

Výroba po n rokoch = počiatočná produkcia × (1 + r/100) ⁿ

Odpisy: Keď sa náklady na produkt každý rok odpisujú o r %, potom jeho hodnota po n rokoch je

Súčasná hodnota × (1 + r/100) ⁿ

Populačné problémy: Keď sa počet obyvateľov mesta, mesta alebo dediny zvyšuje určitým tempom za rok.

Populácia po n rokoch = súčasná populácia × (1 + r/100) ⁿ

Rozdiel medzi zloženým úročením a jednoduchým úročením

Rozdiel medzi zloženým úročením a jednoduchým úročením sa dozviete nižšie v tomto článku

Príklady zloženého úročenia

Niektoré príklady zložených úrokových vzorcov sú,

Príklad 1: Nájdite zložený úrok, keď istina = 6000 Rs, sadzba = 10 % ročne a čas = 2 roky.

Riešenie:

Úrok za prvý rok = (6 000 × 10 × 1)/100 = 600

Suma na konci prvého roka = 6000 + 600 = 6600

Úrok za druhý rok = (6600 × 10 × 1) / 100 = 660

Suma na konci druhého roka = 6600 + 660 = 7260

Zložený úrok = 7260 – 6000 = 1260

Príklad 2: Aký bude zložený úrok z 8 000 Rs za dva roky, keď bude úroková sadzba 2 % ročne?

Riešenie:

Vzhľadom na to,

• Hlavné P = 8000
• Sadzba r = 2 %
• Čas = 2 roky

podľa vzorca

A = P (1 + R/100) ⁿ

A = 8 000 (1 + 2/100)²= 8 000 (102/100)²

A = 8323

Zložený úrok = A – P = 8323 – 8000 = 323 Rs

Príklad 3: Hari uložil Rs. 4000 s finančnou spoločnosťou na 2 roky s úrokom 5% ročne. Aký je zložený úrok, ktorý Rohit dostane po 2 rokoch?

Riešenie:

Vzhľadom na to,

• Hlavné P = 4000
• Sadzba r = 5 %
• Čas = 2 roky

Podľa vzorca

A = P (1 + R/100)ⁿ

tcp a ip model

A= 4000 (1 + 5/100)²

A= 4000 (105/100)²

A= 4410

Zložené úročenie = A – P = 4410 – 4000 = 410

Príklad 4: Nájdite zložený úrok na Rs. 2000 vo výške 4 % ročne na 1,5 roka. Keď sa úroky zrátajú polročne?

Riešenie:

Vzhľadom na to,

• Hlavné p = 2000
• Sadzba r = 4 %
• Čas = 1,5 ( t.j. 3 polroky )

podľa vzorca,

A = P (1 + R/200) ²ⁿ

A = 2 000 (1 + 4/200) ³

A = 2000 (204/200) ³

A = 2122

Zložené úročenie = A – P = 2122 – 2000 = 122

Príklad 5: Aký je zložený úrok z 10 000 na jeden rok pri sadzbe 20 % ročne, ak sa úrok účtuje štvrťročne?

Riešenie:

Vzhľadom na to,

• Istina P = 10 000 Rs
• Sadzba R = 12 % (12/4 = 3 % za štvrťrok)
• Čas = 1 rok (1 × 4 = 4 štvrťroky)

Podľa vzorca,

A = P (1 + R/100) ⁿ

A = 10 000 (1 + 3/100) ⁴

A = 10 000 (103/100) ⁴

A = 11255

Zložený úrok = A – P = 11255 – 10000 = 1255

Príklad 6: Nájdite zložený úrok pri sadzbe 5 % ročne na 2 roky z tej istiny, ktorá za 2 roky pri sadzbe 5 % ročne dostane Rs. 400 ako jednoduchý úrok.

Riešenie:

Vzhľadom na to,

• Jednoduchý úrok IF = 400
• Sadzba R = 5 %
• Čas T = 2 roky

Podľa vzorca,

Jednoduchý úrok = (P × T × R)/100

⇒ P = (SI × 100)/T × R

P = (400 × 100)/2 × 5 úroková sadzba = 5 %

P = 40 000/10 = 4 000 Rs

Čas = 2 roky

previesť reťazec na interger

Podľa vzorca,

A = P (1 + R/100)

A = 4 000 (1 + 5/100)

A = 4410

Zložené úročenie = A – P = 4410 – 4000 = 410

Príklad 7: Nájdite zložený úrok 30 000 Rs pri 7 % úroku zložený ročne počas dvoch rokov.

Riešenie:

• Istina P = 30 000 Rs
• Sadzba R = 7 %
• Čas = 2 roky

Podľa vzorca

A = P (1 + R/100) ⁿ

A = 30 000 (1 + 7/100) ²

A = 30 000 (107/100) ²

A = 34347

Zložený úrok = A – P = 34347 – 30000 = 4347

Súvisiace čítanie:

• Denný zložený úrok
• Mesačný zložený úrok
• Riešenie zloženého úročenia triedy 8
• Zložené úročenie – otázky a odpovede týkajúce sa schopností
• Jednoduchý záujem

Zložené úročenie – praktické otázky

Rôzne praktické otázky týkajúce sa zložených záujmov sú,

Q1. Nájdite Sumu, ktorú je potrebné zaplatiť po 3 rokoch, ak sa požičiava suma 10 000 so sadzbou 4 % ročne.

Q2. Nájdite úrok, ktorý je potrebné zaplatiť po 1,5 roku, ak sa požičiava suma 2 500 so sadzbou 6 % zloženou polročne.

Q3. Vypočítajte si zložený úrok pre sumu 9 000 požičanú pri sadzbe 5 % štvrťročne na 15 mesiacov.

Q4. Vypočítajte si zložený úrok pre sumu 20 000 požičanú pri sadzbe 12 % na 3 mesiace zloženú mesačne

Záver zloženého úroku

Zložené úročenie je a výkonný finančný koncept, ktorý umožňuje investíciám alebo pôžičkám rásť alebo akumulovať sa v priebehu času. Na rozdiel od jednoduchý úrok, ktorý počíta iba úrok z počiatočnej sumy istiny, zložené úročenie berie do úvahy úrok získaný z počiatočnej istiny, ako aj prípadný akumulovaný úrok z predchádzajúcich období.

Zložené úročenie – často kladené otázky

Čo znamená zložené úročenie?

Zložený úrok je úrok vypočítaný z istiny, ako aj z predchádzajúceho úroku získaného počas pevne stanoveného časového obdobia

Ako vypočítať zložený úrok?

Na výpočet zloženého úroku sa najprv vypočíta konečná suma, potom sa odpočíta od istiny, aby sa získal konečný zložený úrok. Suma sa vypočíta podľa vzorca,

A = P(1 + R/100) ^t

CI = A – P

Je zložený úrok pre investorov lepší ako jednoduchý úrok?

Áno, zložený úrok je pre investorov oveľa lepší ako jednoduchý úrok.

Čo je vzorec zloženého úročenia, ak sa denne skladá?

Predpokladajme, že daná istina je P, sadzba je R a časový interval je T rokov, potom vzorec zloženého úroku pri dennom zložení je:

A = P(1 + R/365) ^{{365 × T}}

Aký je rozdiel medzi CI a SI?

Základný rozdiel medzi CI a SI je, že SI je úrok účtovaný zo sumy istiny, zatiaľ čo CI je úrok účtovaný zo sumy istiny, ako aj z úroku akumulovaného z istiny